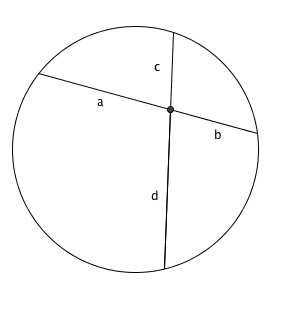
Mathematician: The Intersecting Chords theorem asks us to consider two intersecting line segments inside of a circle (such that each line segment starts and ends on the edge of the circle). Each line segment can be thought of as being divided in two parts by the point where the two line segments intersect (in the image below these parts are a and b for the first line segment, and c and d for the second line segment). The Intersecting Chord theorem says that when we multiply the lengths of the two parts of the first line segment together, we get the same value as when we multiply the lengths of the two parts of the other line segment together (that is, that a*b = c*d). The Power of a Point theorem generalizes this situation to the case where only one side of each line segment lies on the circle, and the other sides of the line segments can intersect each other outside of the circle. The answer you get is a bit different in this case.
One way to think about why the Intersecting Chords theorem is true is because the triangle formed with a and d as two of its sides is a similar triangle to (has the same angles as) the triangle formed that has c and b as two of it’s sides. Because the triangles are similar, that implies that a/d = c/b (that is, the ratio of side lengths should be the same for the two triangles), and if we multiply both sides of this equation by both b and d, we get a b = c d which is just the Intersecting Chord Theorem.
For more info see:
An Explanation of the Intersecting Chord Theorem






