Q: If you could see through the Earth, how big would Australia look from the other side?

The original question was: Relative to the size my feet appear when I’m standing up and looking at the ground, how large would Australia appear if I could see all the way through the Earth and observe its shape?  Also, if we considered my location to be a new “north pole”, how large would the “northern” hemisphere I observe seem relative to the “southern” hemisphere? In other words, due to the direct inverse relation between apparent size and distance, how much smaller does one half of a sphere appear from a point directly centered on the surface of the other half?

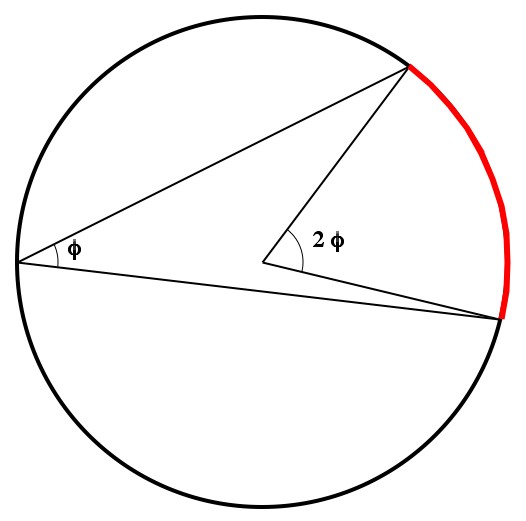
Physicist: This is example of “party trick mathematics”, the kind of math that you can do in your head, but that looks really complicated.  There’s a seriously old theorem from the days when togas meant math (not frat parties) called the “inscribed angle theorem”.  It says that if something has an angle on a circle of 2ϕ when seen from the center of the circle, then when seen from a point on the edge it will have an angle of ϕ.  What’s really surprising is that it doesn’t matter where you are on the circle.  It always works.

The Inscribed Angle Theorem: Surprising, but true.

I estimate that Australia spans about 34°.  Which means that, if you could see it through the Earth, it would take up about 17° of your vision.  Also, it wouldn’t matter where you are on the planet, it would always be 17°.  Unless you’re in Australia.  The size of where ever you are is always 180°.  Unless you’re on the beach or something (90°?).

Lucky for us (people), we all scale about the same.  There are some (literal) rules of thumb that you can use to estimate angles.  From standing, your feet are about 10°.  With your arm outstretched, the width of your thumb is about 1.5°, and your fist is about 7°.

So if you could see Australia through the ground, it would span about two and a half fists-at-arms-length, or a little less than two of your-own-feet-while-standing.  If you could see the other hemisphere (pick one), then it would appear to be exactly 90° across.

What follows is answer gravy:

Finally, for those of you who want to find exact arcangles on the Earth’s surface: If you have two locations at latitudes and , and the difference in longitudes is , then the true arcangle between them is:

Also, if you multiply this number by 6365, then you’ve got the distance between those points in km (as the crow flies).