The original question was: I have a question about the twin paradox. Is it true that faster aging of the twin who stayed at home happens only when the other twin’s spaceship is accelerating/deceleration (btw, does it matter whether he is accelerating or decelerating?)? Consequently, do they age at the same rate when the spaceship moves inertially?
Physicist: The very short answer is: geometry works different in spacetime than it does in just space.
The twin paradox is a result from special relativity that states that if one person, Alice, remains “stationary” and another person, Bob, takes any kind of round trip, then the stationary Alice will experience more time. The twin paradox isn’t a paradox at all, it’s just strange and off-putting (like twins).
In relativity (that is to say: “in reality”) there’s no difference between being stationary and having smooth (non-accelerating) movement. On the surface of it, the only difference between Alice and Bob is that, in order to return home, Bob has to accelerate (turn around) at some point. So is acceleration the secret to the twin paradox? Nope.
In all of the pictures that follow the “time direction” is up, and one of the (three) space directions is left/right.
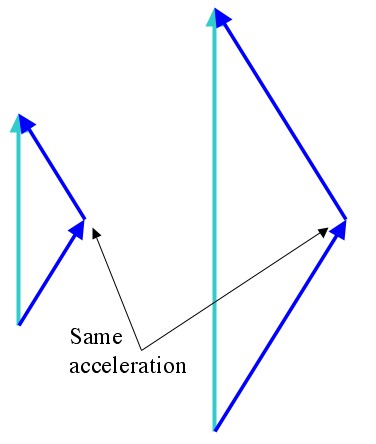
Out and back: In both situations Bob (blue) experiences the same acceleration, while Alice (aqua) sits around on Earth. The only difference is that the second situation involves twice the distance, and twice the difference in experienced time. Acceleration is not what’s important.
The trick is: spacetime doesn’t obey the “triangle inequality”. As a result, the bendier a path is, the shorter it is (that shouldn’t make any sense, so please read on).
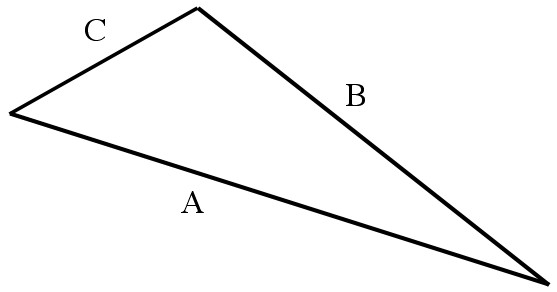
The triangle inequality says that (in space) the sum of any two sides of a triangle is greater than or equal to the third side. In spacetime the inequality can be reversed. One side is often longer than the other two: a round-about route is shorter than the direct route. In this case, A+C<B.
The equation for distance that we’re used to is: 
It so happens that the effects of length contraction and time dilation cancel each other perfectly, so that we can use a new (better) measure for spacetime distance, called the “Interval” or “spacetime interval” or “Lorentz interval”:
(as often as not the sign on the right hand side is reversed, not to worry)
The advantage to the Interval is that, no matter what, the Interval between any two points in spacetime (two locations and times) is always the same, despite relativistic weirdness. Here’s another bonus! The Interval of a path is the same as the amount of time experienced on that path!
No one every really feels like their own position is changing, so:
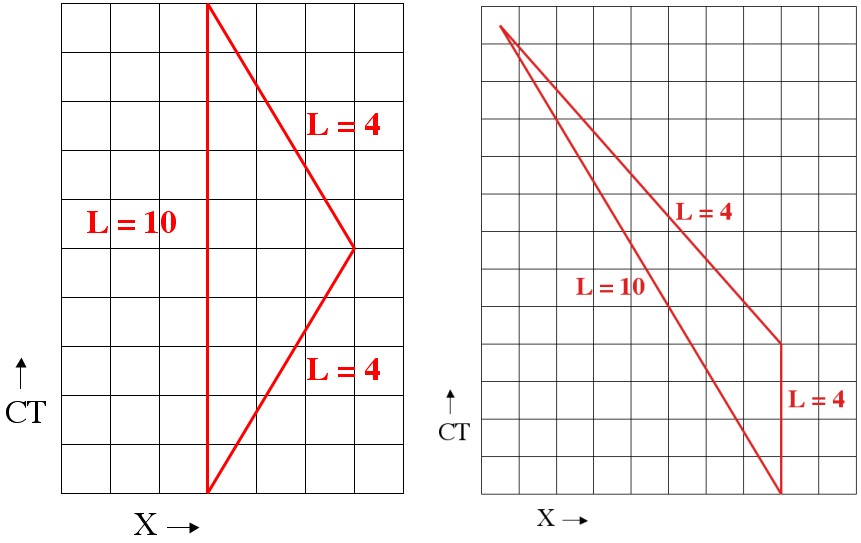
Now all that’s left is to draw a picture and do a little calculating. Here’s an example situation from Alice’s perspective, and then Bob’s (initial) perspective. The difference between Alice and Bob’s velocity is 0.6C (60% of light speed).
The same situation from two perspectives, but since L is invarient you get the same values. Alice experiences 10 units of time while Bob experiences 8 units (since 5^2-3^2=16=4^2).
Hi Alan,
For a layman like me, I can understand what you have just described. But those scientists (or are they?) working in physics area and most likely relativity area, they are still publishing papers arguing against time dilation in the 21st century. Is this incredible? Here I suggest they come to this website and present their arguments. Then we can begin an efficient discussion and maybe we layman can convince them something. What do you think?
if a fast growing plant and animal show us reality
The paradox of twin are not if physica, because the time might not bê physical, because the relative motions and the speeds are not real, because its cannot bê measured, because exist not absolute frame , tô measure the speed concret e. Then the time cannot measure the biológical cells.are just aspects geometrical, for differents curvatures of spacetime
The shortest, simplest and clearest proof of the Twin-Paradox to be no paradox at all. I wonder why people have still been discussing on for years, the case is obviously closed.
Pingback: Q: If time is relative, then how can we talk about how old the universe is? | Ask a Mathematician / Ask a Physicist
hey g
And no one mentioned dear Schrödinger’s cat? So what’s the verdict, is the poor feline still breathing, or only alive in an alternative mathematical world?