Physicist: A lot of things get messed up by relativity, like when and where stuff happens, how massive things are, or how time passes. Length contraction is an effect that literally makes things shorter in the direction of motion. So if something whipped by you from left to right it would be thinner, but just as tall.
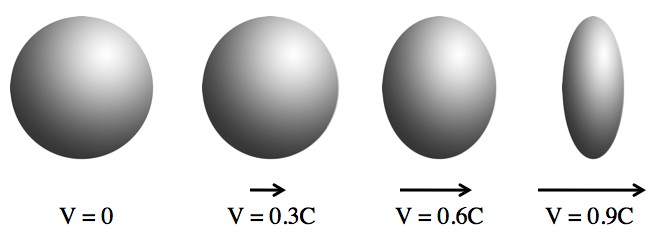
"Lorentz contraction" or "length contraction": Moving objects are shorter in the direction of motion. As with all relativistic effects, this mostly shows up close to the speed of light, C. It is physically real, and not an illusion or trick-of-the-light.
Which begs the question, why is it just as tall? Why doesn’t it just shrink all over, or something?
Well, one of the things that relativity doesn’t change is whether or not an “event” actually happens. So imagine this: you’ve got two hoops spanned by paper, and they’re flying at each other face-on. If the paper in a hoop is torn out, then you’ve got an event that everyone will agree on. No matter where you are or how fast you’re moving, you’ll see that the paper was torn. The only thing relativity affects is when and where that event takes place.
So, pretend that length contraction now shrinks things in every direction.
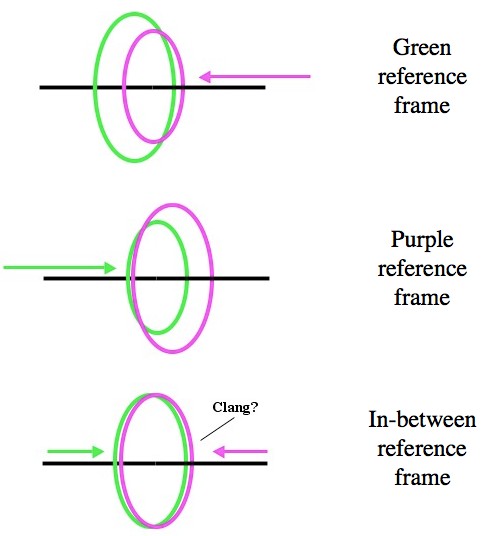
If you assume that length contraction acts perpendicular to the direction of motion you end up with people explicitly disagreeing over events, in a paradoxical kind of way.
If you’re in the reference frame of the green hoop (from your point of view the green hoop is sitting still), then the purple hoop will be smaller and will pass through. The green hoop’s paper will burst, and the purple’s will stay intact. If you’re in the purple hoop’s frame, exactly the opposite happens. And finally, if you’re exactly in between the two frames (you see each hoop approaching at the same speed), both hoops shrink by the same amount and run into each other.
What should be a single event, viewed from different perspectives, is now three different and contradictory events. You can make the effectively identical arguments for enlarging in the perpendicular direction, and even rotation.
Perpendicular special relativistic effects lead to basic contradictions and paradoxes.







Pingback: Q: Why does relativistic length contraction (Lorentz contraction) happen? « Ask a Mathematician / Ask a Physicist
Pingback: Q: How do velocities add? If I’m riding a beam of light and I throw a ball, why doesn’t the ball go faster than light? | Ask a Mathematician / Ask a Physicist
Pingback: Quora
why is it that dimensions perpendicular to motion do not change?
Pingback: Q: How do you prove that the spacetime interval is always the same? | Ask a Mathematician / Ask a Physicist
Pingback: Is Earth Actually Flat? | Youtubers.watch
Pingback: Is Earth Actually Flat? | Woowix
I reworked this example with the claim that contraction occurs ONLY IN the direction of motion. Is this the reasoning you’d use:
1) From the green hoop’s perspective, a slimmer but as tall purple hoop HITS (as opposed to rips through) it
2) From the purple hoop’s perspective, a slimmer but as tall green hoop HITS (as opposed to rips through) it
3) From the center, both hoops hit each other.
Pingback: Is Earth Actually Flat? | www.vcliper.com
Good question. A tearelvr’s speed relative to himself or herself must be zero. However, a tearelvr can measure his or her speed relative to the Sun, and that in general will be non-zero but must be less than the speed of light. However, at relativistic speeds the tearelvr observes length contraction in the direction of motion. From the tearelvr’s perspective the distance between the origin and destination becomes noticeably shorter. From this perspective, the change in distance allows the tearelvr to make the trip at effectively faster than light speed without ever measuring a speed faster than light speed.
Pingback: Is Earth Actually Flat? science video - Life Sciences Discovery - All Sciences Discovered
Pingback: Is Earth Truly Flat? — Follow, Index, Nofollow & Noindex
Pingback: 5 Trippy Implications About Time ~ Fractal Enlightenment
In MM experiment (done in vacuum), number of waves existing on light paths that are diverged by half mirror is the same. Therefore, if light speed (relative to the apparatus) is constant, Lorentz contraction must be denied.
P.S. Sorry, I can not receive E-mail. I don’t have PC.
A passenger car is moving. Two light rays are sent from a source (frequency is constant) set on the floor and are reflected by mirrors set on the roof and are coming back to the source (the light path forms oblong letter V). Number of waves that stays on the path is the same to an observer stands on the ground (because it’s an invariant). This picture will support the emission theory. Not only Lorentz contraction, but also constancy of light speed and relativity of simultaneity will be denied.
P.S. Sorry, I cannot receive E-mail. I don’t have PC.
Allow mw to rewrite previous post (Nov 25) as follows.
An apparatus of MM experiment is working (in vacuum). Suppose that the number of waves existing on the light paths (diverged by half mirror) is the same always (to below decimal point. From the experimental result on interference fringes, this supposition will not be denied). There is an observer moving relative to the apparatus. To the observer, the number of waves is invariable also (it is an invariant). Therefore, if light speed (to the observer) is constant, Lorentz contraction must be denied.
P.S. Sorry, I cannot receive E-mail. I don’t have PC.
Lorentz contraction
In a passenger car, a light source is placed on the floor. Two light rays (frequency is constant) are being sent to the two mirrors on the roof and return (only once : light paths form letter V). Number of waves existing on the light paths is invariant. This passenger car is moving.
How the above is visible to an observer on the ground ? This picture will be incompatible with constancy of light speed, Lorentz contraction and relativity of simultaneity.
Sorry, I cannot receive E mail. I do not have PC.
@hiroji kurihara
The speed of light stays the same from every perspective, but the frequency does not. The person on the ground watching the train go by sees the same number of wave crests and the same speed of light, but the total path length and the individual wavelengths are greater. So they see the light “red-shifted”.
This is called the “Relativistic Doppler Effect” or sometimes the “Transverse Doppler Effect”.
Lorentz contraction
Plain waves of light (wavelength is constant) are coming from the upper right 45 degrees. Two bars of the same length are moving to the right and the left at the same speed. The number of waves hitting the bars is the same. Lorentz contraction is unthinkable.
Tranceverse Doppler effect
On a plane, pararell lines are drawn. On each line, light sources (frequency is the same) are moving in the opposite direction. Imagine light sources form japanese letter エ. Phenomenon tranceverse Doppler effect will not be.
Lorentz contraction
In a moving passenger car, MM experiment is being done. There is a considerable difference in length between two light paths diverged by half mirror. Lorentz contraction will not stand up.
Pingback: Historia Szczególnej Teorii Względności – część pierwsza – AstroNET – Polski Portal Astronomiczny