Q: Why is it that photographs of wire mesh things, like window screens and grates, have waves in them?

Posted on January 13, 2012 by The Physicist

Physicist: There are two major effects that generate waves in pictures. The first is called “aliasing”, and it’s caused by “under-sampling”.  It shows up every now and again when you’re using a digital camera, or when you’re trying to express a picture that contains a regular pattern using too few pixels.  The frequency of the pattern is accidentally read as a different frequency.  The second effect is called a Moiré pattern, and it shows up when the camera’s CCD and what the camera is pointed at disagree about what’s horizontal and vertical.  It’s a problem when the lines in question are around 1 or 2 pixels thick.  Technically, in the context of digital cameras, this is just aliasing again.

Moire pattern from two sets of parallel lines.

Normally aliasing is a problem in analog to digital conversion of sound, but it comes up in a number of places.  There’s a theorem called “Nyquist’s theorem” that states that if the highest frequency in a signal or pattern is X, then you need to sample at a frequency of at least 2X or you’ll get aliasing.  In the case of pictures, the smaller the pattern, the higher its “frequency”, and the higher the pixel count the higher the “sampling frequency”.

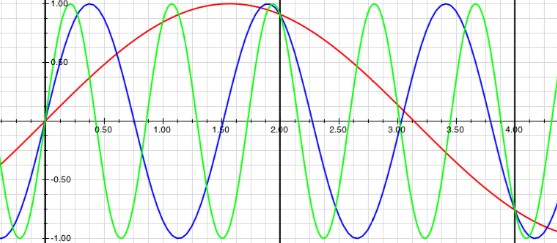
Aliasing: All three of these waves have the exact same value at 0, 2, 4, etc. so if you're sampling every 2, then they all look the same to you.

For example, most people can hear up to about 22,000 Hz (young people can hear a little higher), so digital recording equipment has to sample sound at least 44,000 times per second (44,000 Hz).  In practice most equipment samples even more.  In this case aliasing causes stray sounds that should be above human hearing to show up in the recording.  Very off-putting.

So, if you have a regular pattern of some kind, like bricks, and you take a picture of it, then in order to avoid weird looking waves, you need at least two pixels per brick.

Left: Under sampled. Right: Sampled enough.

In the picture above the “high-frequency bricks” are aliased and appear to have “low-frequency ripples”.  The effect goes away when you use a zoom lens or a higher resolution, because the sampling frequency increases.

It’s a lot more common to see aliasing show up in digital sound recordings and in video.  The standard 24 frames per second (a sampling frequency of 24 Hz) means that things that repeat faster than 12 times per second will be aliased.  The most jarring example of video aliasing is the “wagon-wheel effect”.  A spinning object on film can appear to be turning at the wrong speed, turning backwards, or even sitting still.  There are some dramatic examples: here and here.

The easiest way to completely avoid aliasing and Moire patterns is to use analog cameras and actual film.  That said, the digital cameras today have such high resolutions that aliasing is pretty unusual.

Answer gravy: So, why do you need to sample at double the frequency, and not just at the frequency?

A wave can be described as x(t)=A\sin{(2\pi ft+\phi)}, where A is the amplitude (size), f is the frequency (how fast it oscillates), and ϕ is the phase (slides the whole thing back and forth).  If all you can do is sample the wave, at times 0,T, 2T, 3T, \cdots (t=nT), then you get a string of values x_0=x(0),x_1=x(T), x_2=x(2T),x_3=x(3T),\cdots.  By definition, the sampling frequency, fs, is 1/T.

So, x_n = A\sin{\left(2\pi f(nT)+\phi\right)}=A\sin{\left(\frac{2\pi}{f_s}nf+\phi\right)}.

But check it: you can add a multiple of 2π inside of sine whenever you want and it doesn’t change anything (sine is “2π periodic“).  So:

\begin{array}{ll}x_n=A\sin{\left(\frac{2\pi}{f_s}nf+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}nf+2\pi nk+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}nf+\frac{2\pi}{f_s}nkf_s+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}n(f+kf_s)+\phi\right)}\end{array}

This means that f \sim f+kf_s.  That is, waves with frequency f, f+fs, f+2fs, etc. will all give you exactly the same set of measurements (xn).  You cannot tell them apart.

But more than that:

\begin{array}{ll}x_n=A\sin{\left(\frac{2\pi}{f_s}nf+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}nf-2\pi nk+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}nf-\frac{2\pi}{f_s}nkf_s+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}n(f-kf_s)+\phi\right)}\\=-A\sin{\left(\frac{2\pi}{f_s}n(kf_s-f)-\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}n(kf_s-f)+\pi-\phi\right)}\end{array}

This type of aliasing is responsible for wheels appearing to spin backward on film.

The “π-ϕ” is different from “ϕ”, however this new phase doesn’t impact the frequency (frequency is what you see and hear).

So, f \sim kf_s-f as well as f \sim kf_s+f.  For succinctness: f \sim kf_s\pm f.

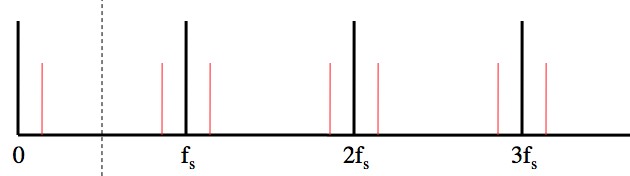
Because of the layout of frequencies that all appear the same (red lines) you can only trust frequencies below half of the sampling frequency, fs.

So check it!  If you have some way to guarantee that the frequency you’re measuring is below \frac{f_s}{2} (using filters or something), then what you see between 0 and \frac{f_s}{2} will be correct.  Otherwise, what you see between 0 and \frac{f_s}{2} may be an alias of a different, higher frequency.

Clearly, most signals aren’t a single frequency the way a sine wave is.  But that doesn’t really matter, since you can write a signal out as a bunch of sine waves added together, and the same math applies to each of those.

This entry was posted in -- By the Physicist, Math. Bookmark the permalink.

3 Responses to Q: Why is it that photographs of wire mesh things, like window screens and grates, have waves in them?

  1. Alejandro says:
    June 13, 2012 at 4:02 pm

    Great article! I just wanted to point out that 22 kHz is way above the frequency that humans can hear; the standard number it’s around 20 kHz and this is only in very healthy and young humans, because this greatly decreases with age (both for natural and artificial reasons like going to clubs every weekend) being common that a middle age man can hear only up to around 15 or 16 kHz (I’m an audio engineer and, believe me, I wished this wasn’t the case). You can test your ear’s frequency response with easily available tools such as this http://www.noiseaddicts.com/2009/03/can-you-hear-this-hearing-test/

    Now the extra kHz that the sampling process requires (like the 44.1 kHz that CD’s are sampled on; which is just a standard number determined by Sony) obeys to the fact that in order to avoid aliasing a Low Pass Filter is applied (which is essentially a filter that stops every frequency above a specific point) and this requires a fade out, i. e. these devices can’t abruptly stop the frequencies above the given point. This is why the sampling process needs an extra kHz to operate.

  2. Deson Bowenford says:
    September 10, 2012 at 10:41 pm

    A wonderful example of the stroboscopic effect can also be seen here. http://www.youtube.com/watch?v=rVSh-au_9aM

  3. Tarek Kandil says:
    June 25, 2014 at 3:31 am

    @Alejandro – I think you’re talking about the highest pitch we can hear at 20kHz… bats can go way higher etc…

    but I think the article meant sample rate… as in we slice up sounds we hear into 22,000 discrete chunks to ‘animate’ the sound. Which is why the samplerate at which things are recorded is about double that, recording digitally at a 44.1kHz samplerate will slice a sound into 44 thousand chunks of sound, so we hear it super smoothly … bit confusing when talking about the pitch we hear, which is 20Hz – 20kHz…

    I’m confused… slightly.

    Tarek

Leave a Reply

Your email address will not be published.