Physicist: Singularities are just artifacts that fall out of math. They show up a lot in theory, and (probably) never in nature. The “singularities” most people have heard of are black hole singularities.
In practice, when you’re calculating something in physics and you find a singularity in your calculation (this happens all the time), which usually looks like “1/x”, then that means that there’s a mistake somewhere, or you’re looking at something that never happens, or there are physical laws or effects that haven’t been taken into account.
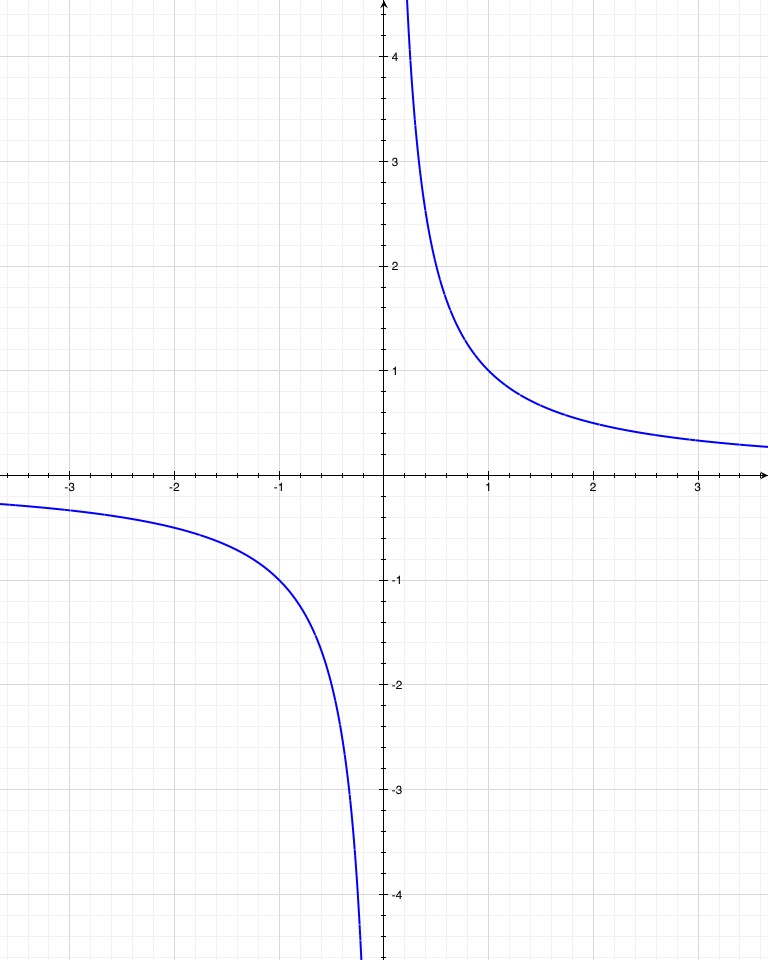
The simplest mathematical singularity: 1/x. The closer you get to zero, the more 1/x blows up, and at x=0 the function is undefined.
For example, when you drain water from a tub or sink the water will spiral into the drain. A back of the envelope calculation (based on known principles) shows that the speed, s, that the water is moving is 
One of the slick tricks that water uses to avoid spinning infinitely fast at the center of a vortex: not being there.
Even when you’re deep underwater there are outs; turbulence, cavitation, that sort of thing.
A slightly more obscure example is the energy of a charged particle’s electric field. If you have an electron just sitting around, the energy, E, of its field outside of a distance, R, from the electron is 
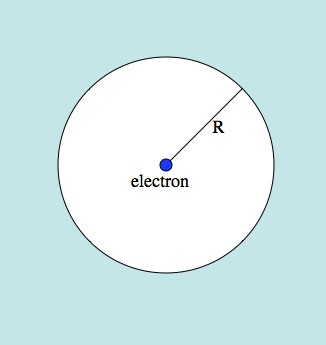
The electric field being considered is the light blue area. The most intense part of the field is close to the electron, so as R gets smaller and smaller, the total energy gets bigger and bigger.
Most of that is just equation porn. The important bit is the “
The whirlpool thing and the electron thing (and hundreds of other examples) are examples of singularities that show up in the math, but can be explained away through experiment and observation, and shown to not be singularities in the physical world.
In general relativity, the shape of spacetime near a spherical mass is given by:
Now, unless you’re already a physicist, none of that should make any sense (there are reasons why it took Einstein 11 years to publish general relativity). But notice that, as ever, there’s a singularity at r=0. This is the vaunted “Singularity” inside of black holes that we hear so much about.
Something like a star or a planet doesn’t have a singularity, because this equation becomes invalid at their surface (this equation is about the empty space around a mass). But, for a black hole the gravity is so intense, and spacetime is messed up so much that it looks as though there’s nothing to stop matter from becoming infinitely dense. However, unlike the singularity over the drain in your sink, the singularity in a black hole can’t be observed. Which is frustrating.
I suspect that what we call the singularity in black holes either doesn’t exist (there is some law/effect we don’t know about) or, if cosmic censorship is true, the nature of that singularity both doesn’t matter and can’t be known, since it can never interact with the rest of the universe. There are some theories (guesses) that would fix the whole “black hole singularity problem” (like spacetime can only get so stretched, or some form of “quantum fuzziness”), but in all likelihood this is just one of those questions that may never be completely resolved.
The whirlpool photo is from here.
Great article, I’m not physicist but always enjoy the manner that attack the problems, in particular the form so fluid that the article was written, I try to incorporate that style when do my document, unfortunatly I only have read this style in english and have some problems to incorporate in spanish xd.
Anyway thanks for the great article
Interesting and very informative article. I think the energy equation is incorrect. It’s only epsilon not epsilon square.
You are completely correct. Fixed!
I came here looking for an answer about black holes that involves several singularities I suppose. Initially I thought that black holes have a singularity where all the matter occupies the same point in space. Given that premise, I was confused about the spin of a black hole. If a black hole inherits its spin from the star it was formed from and spins faster due to conservation of angular momentum, then wouldn’t the singularity have an infinatly fast spin? Since there are black holes with “not infinite” spin, then does that imply that the matter didn’t collapse to a single point, or is it, like in the article, something else we don’t understand going on? And finally, I’d we could observer the spin of a star before it went supernovae and the spin of the resulting black hole, what would you suppose the difference would tell us about the interior if anything?
I have a couple questions about the supposed singularity in a black hole and the curvature of space time:
1) What is curved space-time? Time is curving with regards to a spatial dimension? If so does a particle traveling to a center of a blackhole with a finite speed actually reach a singularity or just move forward in time?
2) Wouldn’t a distribution of mass over curved 4 dimensional space make it impossible to have infinite density if a most of the mass were at different time coordinates?
3) If Hawking radiation is correct doesn’t that seem to suggest intuitively that there is no singularity in a black hole?
If Singularity does exist in nature it will eventually break the law of conservation of Mass-Energy, conservation of charge etc… of the Universe, because nothing can escape from Singularity. and moreover how can a zero volume can occupy Infinite density, does it make sense at all…..
If Singularity does exist in nature it will eventually break the law of conservation of Mass-Energy, conservation of charge etc… of our Universe, because nothing can escape from Singularity. And moreover how can a zero volume can occupy Infinite density, does it make sense at all ? Thus all the Matter entering into the singularity will end up there. Is it necessary that a ” Black-Hole” should have a Singularity ? or Is a Singularity is just a mathematical frame-work and might not exist in realty. There is no, proper definition of Singularity. Can’t we construct a Black-Hole model which doesn’t require any sort of Singularity…….?
When you spin a quarter, right before it stops the quarter’s axis of symmetry’s rotation relative to a central axis is unbounded. I had a professor who verified this with a couple grad students using a vacuum chamber, laser, reflective disk and really smooth surface.
This is the closest i’ve thing I heard of to an actual physical finite-time singularity.
http://www.ncbi.nlm.nih.gov/pubmed/12443243
If space is infinitely divisible then there is no smallest size. The volume cannot reach zero. Just like you can’t reach infinity. The black hole will just shrink forever and never attain zero volume. If it always has a volume there can be no singularity.
It sounds like your saying that a singularity is like water down the drain. Now depending on which hemisphere your in water spins right or left. However if everything that goes into a singularity if it stays in this plane of reality . It would mean that so much is compressed into one point making pretty impossible. However like a drain . Do singularity’s empty into another plane of existence ? Or is it so heavy that it able to just keep packing material in one space?
Probably the most familiar example is walking from one spot to another. Theoretically, the intervening distance can be divided to infinity…first taking half the distance, then half that, then half that and so on. But in day to day experience we traverse the distance without incident.
Very interesting article. No, I’m not a physicist but your explanation cleared now my understanding: singularities don’t exist in reality
If a point singularity is shrinking into less space, couldn’t it be said that the matter in it is in motion flowing towards its’ center? If particles of matter are all flowing towards the center of the object containing the singularity, won’t those particles eventually collide? Does this collapse in volume accelerate matter? If the particles of matter do accelerate, could they exceed the speed of light before colliding?
There are various ways to say what the author says, I guess, but I’m a mathematician and want to say it this way: The General Relativity equation quoted, with a 1/r term, is NOT even a mathematical equation at r=0. That is, the equation has no mathematical meaning at all at r=0 because division by 0 is not and can not be defined mathematically in any way. The problem is LOGICAL, not physical. The equation can be a valid math and physics equation for r as near to 0 as you want, but is nothing at all except a nonsense statement at r=0. Maybe it’s good poetry; I don’t know, but it has nothing to do with mathematics. Therefore, if the expression r=0 can even truly have physical meaning to a physicist in this situation, then he or she MUST find some other equation to describe that meaning. The universe does not have to strain or sneak around here; the physicist simply has to find a different equation which has actual mathematical meaning. Of course I do not know what that equation needs to be, but that’s not my problem!
Yay! This finally explains away needing a moving singularity for a moving black hole.
Does planck size apply in a black hole? If yes then does that rule out singularities?
Pingback: Q: Why does gravity pull things toward the center of mass? What’s so special about the center of mass? | Ask a Mathematician / Ask a Physicist
What I have been wondering about is. If a singularity is infinitely dense.
Does that imply space time is stretched infinitely? If so can anything
ever reach the singularity? An object might have an infinite distance to travel at a
finite speed, assuming C still holds.
Also if time slows in a black hole. Does that mean time slows infinitely at the
singularity. So again it might take an infinite amount of time to reach the
singularity, at least to an outside observer. So this leaves me wondering
if singularities don’t exist because the falling matter keeps pushing
the singularity farther away in space time.
Great explanation; thanks.
Just a few comments.
Chris Baird provides another good explanation at:
http://wtamu.edu/~cbaird/sq/2013/09/13/does-every-black-hole-contain-a-singularity/
Jason says: “Now depending on which hemisphere your in water spins right or left.” Not true.
Pierre Pero says: “So again it might take an infinite amount of time to reach the singularity, at least to an outside observer.”
Infinity is not a number, so you cannot have “an infinite amount” of anything.
Pingback: Zeno, Paradox, and Contemporary Confusion
In 3 dimensions plus time, a 3-ball “sheet”, or “brane”, has a singularity.
Black hole singularities are only able to be understood if one first understands a 3-ball.
The topology in question is fully described by US Patent # 4,138,744. And I should know because I am the inventor.
An entire 3-ball cannot be “seen” by human eyes.
Even a 3-ball sheet or brane requires one to understand the entire family of structures for the whole topology to be understood.
A 3-ball has a 3-dimensional geodesic, or hyperedge, and also has a singularity, which can also be called its “vertex.” A 3-ball also has a non-orientable “side”. That is, a 3-ball sheet has one vertex, one 3-dimensional geodesic “edge”, and one non-orientable “side.” The entire infinity of this surface structure would be a whole 3-ball.
A 3-ball (the 3-dimensional surface of a 4-dimensional “solid”) is to a regular ball (like a basketball, a balloon or a soap bubble), as a regular ball (the 2-dimensional surface of a 3-sphere solid) is to a circle (the 1 dimensional “surface” of a 2-sphere “solid”).
One cannot actually comprehend the topologically similar singularity of a black hole without understanding several dimensions of “balls”, from 3-ball sheets in 3 dimensions, and related 3-balls in at least 4 dimensions, up through 4-balls, 5-balls, 6-balls and a full 7 dimensional space. After all, they are all involved.
If you have not had your coffee, or the otherwise required red pill, then you may not understand this little set of statements. Too bad.
If you are a typical sled dog physicist or mathematician, whether or not you are on a typical sled dog team, where only the lead dog gets a change of scenery, then you are almost certainly hopelessly blind to any of this insight.
So, you have a choice. Drink some coffee, and start learning about the 3-ball, or just forget about black hole singularities and their topologies. It’s way over your head. You need, as the expressions goes, a tall hat.
Michael
Fascinating! I’ve had my morning coffee, though no red pill, whatever that is.
(Disclaimer first: My use of caps never denotes anger, only emphasis, like an “accent.”)
Yes, this post is definitely way over my head, in the sense that it is mostly incomprehensible to me. I do understand some parts, probably, with my present background, but not the parts Michael probably hopes the most that I would understand. I’ll leave that understanding to those with the right background, or to those with the resources to research the topic in the ways Michael suggests, but in the meantime, I have no reason to doubt the correctness of everything Michael says, though, as I said, I don’t have at the moment the personal power to vouch for it
All this leaves me a little unsure of exactly what is Michael’s main point though. One guess I have (And Michael, please fee free to correct me if I’m wrong) is that he is suggesting that there CAN indeed be a genuine physical realization of at least one form of what we mathematicians call a mathematical singularity, in a black hole, and that to understand this realization one needs to understand the topology he leaves tantalizing hints about here. Again, as I said, I’m not qualified to make comments yet on that statement, or, for that matter, to even be sure that it IS the main point Michael is getting at.
However, what I like to emphasize at a simpler level, and as perhaps a “standard dog sled mathematician” and logician, is some simple reasoning from basic principles which I believe you will be able to understand right here without any further research (at least if you are a typical mathematician or physicist), and which clarifies what I mean when I say that at least certain types of mathematicians’ singularities can NOT possibly be realized in the physical world.
Not to exhaust the possible topic, but within the limitations of commonly understood usage for functions and singularities, a math function, usually expressed precisely by an equation or a possible group of equations, has a singularity at a specific point in the domain of the function, when it is not possible to use the relevant defining equation of the function in question at that particular point in question, although it is possible to use this same defining equation near to the problem point. “Not possible” means that we can not use logically coherent math definitions to properly express the function according to the given equation.
This usually means, and probably means in most physicists’ discussions involving black hole central singularities, that the equation “breaks down” because a formal, grammatical division by zero is forced at the domain point of singularity. For example, this happens when we try to use the equations of General Relativity to describe this singular point. Now, it is NOT that we mathematicians “forbid” division by zero because we are Stalinists, but rather that it is simply impossible to DEFINE a concept for division by zero which is logically coherent and also consistent with the rest of arithmetic when other numerical inputs are used.
Once we’ve restricted ourselves to this context and are considering specific equations with this specific type of singularity, then we recall right away that there are TWO types of singularities within this framework typically referenced by mathematicians: removable singularities and non-removable singularities.
I have no doubt that removable singularities may exist perfectly well in physical situations. With a removable singularity, the function’s defining equation becomes unusable at the singularity, but it becomes easily possible to nevertheless define the actual value of the function at that point by direct specification in such a way that certain desired properties of the function under question are preserved, and these properties are usually continuity, differentiability, and perhaps several or infinite orders of differentiability. Thus, for example the function defined by the equation y=(5x)/x with real domain and range, has an obvious singularity at x=0 but it is removable because we can simply define y as 5 at that point, preserving continuity and infinite orders of differentiability.
However, the function y=1/x does not allow such a removal at x=0. This point is thus a non-removable singularity of this function. Sure, we can define any arbitrary, directly specified value for the function at x=0 which we may wish, for example, y=17, but then we lose continuity, differentiability, and other desirable qualities of our function at that point. Also, if we happened to be modeling a physical system with this same function y=1/x, then by choosing y=17 at x=0, there is no guarantee that we would be modeling correctly the PHYSICAL system any longer at x=0. The posited physical system in question MAY HAVE an actual numerical value, finite by definition since all real numbers are finite, at x=0, but our equation y=1/x does not tell us what that value is and we would need other, probably empirical, physical information to ascertain it. IF the physical system in question did actually have this strange new value at x=0, e.g., y=17, then the question of a singularity at that point would indeed be resolved, albeit with heaven only knows what consequences for the laws of physics there. Still, we can at least logically conceive of such a strange possibility, which would violate expected laws of continuity, differentiability, etc..
So what’s the point; or what’s my overall point in this response? My point is that once you are modeling a physical system (or any system, math or otherwise) by means of a specified equation, and that equation becomes impossible to use at a certain point in the domain of the function (and thus the domain of interest to the physicist) by virtue of causing a NON-REMOVABLE singularity, then regardless of any other assumptions, topologies, etc., it becomes impossible for that singularity to exist in a physical sense.
Now, that last phrase, being expressed only in the somewhat imprecise language of English, sill needs some explanation and clarification, if we are to try to relate it to our supposed specification of Michael’s main point. What we are saying is that, yes, it is at least conceivable that the equation correctly models the physical system at points other than the singularity point, but that SOME SPECIFICATION OTHER than the equation will be required to provide a logically coherent, genuine mathematical description of the system at the point of singularity. For example, the function in question might obey, for some reason, y=17 at the pathological point. But then, continuity, differentiability, and other desirable qualities of the function will go by the wayside at that point. It is also possible, or alternatively possible, that the original equation in question, which gave rise to the non-removable singularity, will be found to be incorrectly modeling the physical process, not only at x=the singularity point, but anywhere NEAR the singularity point, and so a new equation may be required, and thus a new theory in that neighborhood (“Quantum gravity”?).
Either way, the non-removable singularity can NOT properly model the physical process at the singularity point x IF we are required to continue to use the defining equation which was assumed valid at other points, at the singularity point, because we will then be stuck with a formal expression for y at the singularity point which does not mathematically or even logically define anything. The equation y=1/0 LOOKS LIKE a math expression and equation but it IS NOT ONE.
So, to summarize, a non-removable singularity in a function CAN NOT OCCUR in the sense that either 1) The function at the singularity point must satisfy a completely different DEFINITION than the one given by the otherwise valid equation for the function, e.g., an “arbitrary” but precisely specified direct value such as y=17, which forces violation of desirable (desirable to the physicist as well as to the mathematician) properties of the function at that point, such as continuity and differentiability; and thus likely forces violation of other physicists’ laws; or 2) The defining, modeling equation ALL AROUND THE OFFENDING POINT, i.e., in what mathematicians call a neighborhood or open ball around the point, will have to be CHANGED in a dual effort to both a) correctly model physically the process which is occurring, and b) preserve desirable functional properties of the local and global environment such as continuity and differentiability.
Given the precise descriptions, definitions and logical flow I have just provided, the meaning of the phrase “a mathematically non-removable singularity is impossible in a physical system” is thus clear. It’s impossible because it is not even LOGICALLY AND MATHEMATICALLY POSSIBLE. What is logically and mathematically impossible is certainly physically impossible, at least if we are to remain in the realm of science and logic rather than the realm of poetry and philosophy. Finally, I believe everything I have said is NOT inconsistent with what Michael is saying, but we would need Michael to explain how and why.
Pingback: Laurent and the Dirac Problem – fauxmat