Physicist: “e” shows up on its own a lot, and the frequent appearance of the natural log, ““, follows from that. Almost all of the uses and importance of e and ln are from results in calculus, but those results are so far reaching that they’ve become the standard and have worked their way into everything. If you’re in pre-calculus, or economics, or some other course that may not involve calculus directly, then chances are that you could just as easily be using log10 or log2 instead of
and it wouldn’t make much difference (as long as you’re consistent). Without calculus they’re not particularly special. However, when you start using derivatives and integrals (calculus) you find that e and the natural log are indispensable and surprisingly natural.
The derivative is an operation that takes a function, , and spits out a new function,
, that tells you what the slope of
is. ex has the remarkable property that the derivative doesn’t change it, so at every point on its graph the value of ex is also the slope of ex at that point.
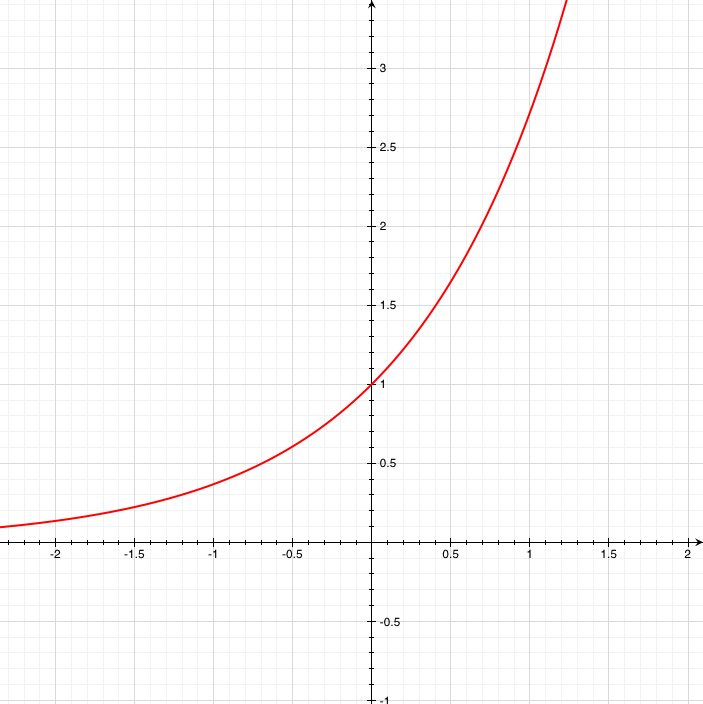
Y=ex: At every point on this curve the slope is equal to the height. For example, at x=0, the height is 1 and the slope is 1 (45°).
While it may seem strange to study an operation in terms of what it doesn’t affect, this idea is the backbone of a lot of mathematics. Fixed points are tremendously important for things like chaos theory and a lot of computer algorithms, and eigenvalues and eigenspaces are about the only way to do linear algebra (which, again, is freaking everywhere).
The other stunningly important property (actually tied up with the calculus property), is that e shows up in Euler’s equation, . This property makes complex numbers useful, and leads into Fourier analysis, which is also in damn near everything.
What follows is mostly calculus.
The three most important properties of e that make it show up all the time are
1) and
2) is the derivative of itself
3)
#1 shows up every now and then. For example, the probability of something happening at least once in N tries, if it has a probability of 1/N of happening each time, is . Also, you can use it to find the actual value of e:
. But generally #2 and #3 are a lot more important.
Technically, these are all the same property, and that property is that ex can be expressed in a very particular way:
Notice that if you differentiate this using the power rule, then every term ratchets down and you end up with exactly the same thing. For example, .
Using this “self-derivative” property of you can show that
. So, when
you get a weird extra ln(A) floating around.
You can also find the derivative of :
.
But this means that the anti-derivative of 1/x is ln(x) (which is good to know) and not some other less natural logarithm. So, anytime you want to find the integral of 1 over some polynomial you’re going to see lots of natural logs.
There are more examples of e’s and ln’s showing up in calculus than there are mathematicians to express them, but long story short; what is tremendously useful in “higher” math trickles down to making an arbitrary choice in “lower” math.







And the most beautiful mathematical formula: e^iπ=-1
Oops! You left out the “i” in the left half of Euler’s equation when you first quote it above.
I believe that your link to eigenvalues and eigenspaces is broken.
Fixed. Thanks!
Great post, thanks. Actually economists are very fond of e and ln for lots of reasons, including the ones you mention (we use calculus too) along with others. For example, we like that ln(1+x)=x (approximately, for small x); this is nice for dealing with interest rates. Also (and related), we like that ln differences approximate growth rates.
Big fan of the blog.
I forgot about the small value approximations! Good point.
I think, for me, the reason why e is so “nature” is (e^x)’=(e^x). This makes y(x)=y(0)*e^kx the solution of the equation y’(x)=k y(x), in which y is the relative grow(decay) rate . we define many things with units, which makes those thing “less essentially natural”. However, the relative grow(decay) rate k doesn’t change no matter how we change the units. It’s more “essentially natural” than values we defined with units. Therefore e is more “essentially natural”.
I enjoyed reading this, thanks! I’m just wondering how often an exponential function is used in science as a fit to an observed phenomenon, when actually what is occuring is a power law? For example, in acoustics there was an adoption nearly a century ago of log10 for expressing sound levels in decibels. But there’s no logical reason that I can see for doing this. Sound pressure decreases with distance as the wave front widens. That’s not exponential in origin, it’s a power law. So we end up with legacy exponentials (which are nice and easy to work with, of course) but don’t make sense in the models.
In another blog I read recently the author referred to the growth of bacterial colonies as often being modelled by an exponential. Yet I can’t see why this would occur, when the multiplication of bacteria is (crudely) just a power series.
So, I’d love to hear your thoughts on this. I’m intrigued to know if a member of the mathematical community is uncomfortable with scientists incorrectly using exponentials of the form e^ax when actually what they have is something like c^bx (and c is not e!)
thanks
Andy
@Andy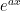 instead of
instead of  . For example,
. For example, 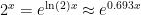 .
.
Whenever you have a situation where the rate that thing increases changes is proportional to the amount of that thing present, then you’ve got an exponential. Bacteria is a great example. The more bacteria there is, the more bacteria is reproducing.
It turns out that all exponential functions are more or less the same, so I don’t personally mind if someone uses
The decibel thing is a bit different. Often we find that something has a very wide range of possible values, where we might regularly talk about “0.000001” of something and “100000” of something a moment later. For example, a rocket launch is around 100000000000000000 times louder than leaves rustling. Using a logarithmic scale (like decibels) we can put both extremes on a graph without practically everything but the most extreme examples being crowded together at the bottom of the graph.
One of the interesting things about e is interest. If you deposit a £ for a year at 100% simple interest, you would have £2 at the end to the year. If you compounded half yearly, you would have £1.50 after half a year and £2.25 after the full year. Similarly compounding quarterly would give you more – £1.25 after 1 quarter, £1.5625 after 2 quarters, £1.953125 after 3 quarters and finally £2.44140625 after a year. If you were to compound more and more frequently the sum would grow and eventually if the interest were to be compounded continuously you would have £e at the end of the year. If the annual interest rate is x%, the amount after one year’s continuous compounding is £e^(x/100)