Physicist: This is a surprisingly subtle question.
It certainly impossible to create new energy, but there’s nothing to stop you from piping energy from one place to another (say, by running hot water from a boiler to somewhere else). The case of sunlight and a lens is just a matter of controlling where the energy is going in a slightly more abstract way. Focusing light from the Sun doesn’t decrease entropy, because what a lens does (this is a little hand-wavy) is to exchange “direction information” for “position information”. The light from one direction (from the direction of the Sun) gets brought together in one position (the focus).
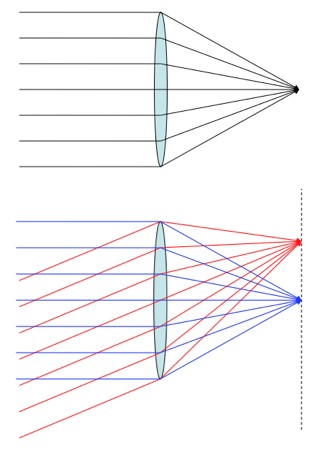
Perfectly parallel light can be focused at a point, but light from different directions focus at different points. Light from multiple directions can’t be focused to one point.
So, if the light from the Sun weren’t so parallel we wouldn’t be able to use a lens to focus it so well. This is why, on a cloudy day, you can’t burn things with a magnifying lens, even when it’s fairly bright outside. The energy is still there, it’s just scattered.
A little surprisingly, focusing parallel light to a point does not change the entropy of the light, and there’s a cute way to show that. A good rule of thumb for entropy is, “if you can reverse it, then the entropy is constant”. In this case, were you so inclined, you could put a second lens after the first that “re-parallelizes” the light.
The act of focusing parallel light is reversible (here’s how), so it doesn’t increase entropy.
It seems as though there should be some way to bring together lots of light beams using lenses and mirrors and… optical cables or something, that would allow you to get a tiny region as hot as you want. But as it happens: no. This is yet another example of the universe having an obnoxious no-go law.
There is a general thermodynamic rule which says that you can never focus energy in such a way that the target is hotter than the source. So, no matter how many mirrors and lenses you have, you can never focus sunlight in such a way that it’ll be hotter than 5800K (the surface temperature of the Sun), but you can get close. In practice that isn’t too useful, because machines tend to break at surface-of-the-sun temperatures.
If you were in the bright spot you’d see a bigger image of the Sun through the lens. With more directions that end in a hot source, the focal point gets hotter.
A good way to think about this is to imagine yourself meandering about in the surface of the Sun, and then imagine yourself lounging at the focus. If you were in the upper layers of the Sun, you’d notice that in every direction you look there’s material radiating at around 5800 Kelvin. As a result, you’d find yourself equilibrating to that same temperature (and burned up real good). If you were at the focus of an elaborate set up of mirrors and whatnot, then you’d be in the same situation, with every direction you look ending with the Sun. And the result is the same.
It feels like there should be some way to cheat, but there just isn’t. If you could find a way to get your target hotter than the source, then you’d have yourself a genuine over-unity device!
The magnifying glass picture is from here.
Are you sure you get an over-unity device? Because if you focus you’re energy, matter around the focus will not receive that energy.
You just have higher energy-density, not more total energy. Is there any proof/experiment of that statement? I just don’t this as impossible, nor useful.
You’d be able to pump heat from a low temperature to a high temperature system at no cost whatsoever. Then you just plug in a regular heat engine (of whatever form) to catch the flow of enery back to the lower temperature system, and you’ve got free usable energy!
Still, that doesn’t make it over-unity. You just transformed energy! The low temp system got cooler, and so did the high temp. It doesn’t mean it’s more than what you had at the beginning.
The point being it would be possible to extract energy from a low temp source, making it cooler and cooler. Now that I think about it, this might decrease entropy or something like that. Bah, I never liked thermodynamics much, anyways
But still, I wonder from which equations this can be proven, since conservation of energy isn’t necessarily the problem.
Here’s a load of mirrors that reflect sunlight to get up to 3,500 degrees C which is pretty cool!
http://en.wikipedia.org/wiki/Solar_furnace
What if we surround the sun with a Dyson Sphere covered in mirrors that reflect all of the light from the surface of the sun to one point on a small asteroid?
It’s harder to keep track of why a more complicated model like that wouldn’t work, but the idea is the same. Each of those mirrors would have to deal with light from a wide range of angles, and that means that they wouldn’t be able to focus very well.
Is there some sort of way to quantify your ideas of information about position and direction?
Imagine a point M, whose position is being measured several times, within a set of different possible boundaries:
W—M—X——-Y——-Z
The information content of the measurement I(W,Y) is related to the information content of the measurement I(W,Z) as
DeltaI = k*ln((Z – W)/(Y -W))
And to I(W,X) as
DeltaI = k*ln((X – W)/(Y – W)
Which is negative.
I imagine the same is true of momentum, where momentum is considered in terms of its magnitude on a number line.
Also, what if the Dysonsphere is
a. Contracting
b. cleverly shaped and rotating, with its mirrors potentially also rotating, in such a way as to bring two seconds of the sun’s energy to the asteroid in one second.
c. Using some of that energy to pump heat from the rest of the sun onto the asteroid
Or
d. The asteroid is contracting.
That’ll do it. But keep in mid that you have to do work to contract the sphere. Similarly you can raise or lower the temperature of any system if you have access to pumps that do work.
Oh, hey Physicist, magnitude of momentum on a number line wouldn’t cover all of the information in I(momentum measurement) would it?
I(max inertia, min inertia) + I(theta, psi) = I(p-observed)
…where theta and psi are spherical coordinates, seems plausible.