Physicist: Because calculus.
When you first start doing trigonometry the choice between radians, degrees, turns, or hexacontades is a matter of personal preference. Most people use degrees because most other people use degrees (and other people seem pretty on the ball). But when you get to calculus using radians is the most natural choice; anything else is just a headache waiting to happen.
To see why you have to get to know the unit circle.
The unit circle. “Unit” means “1” and refers to the radius.
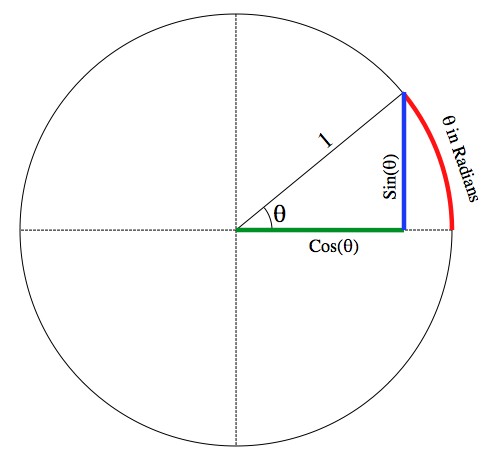
Start with a unit circle with a horizontal line through it and a radius (“a radius” means a line from the center to the edge somewhere). The definition of sine and cosine of the angle between the radius an the horizontal line are in the picture above. SOH CAH TOA is easy in this case because the hypotenuse is 1.
When you use radians you’re describing the angle by using the length of the arc it traces out on the edge of the unit circle. The circumference of a circle or radius R is 2πR, so (since R=1 on the unit circle) the full circle is 2π radians around. That is: 2π radians = 360 degrees.
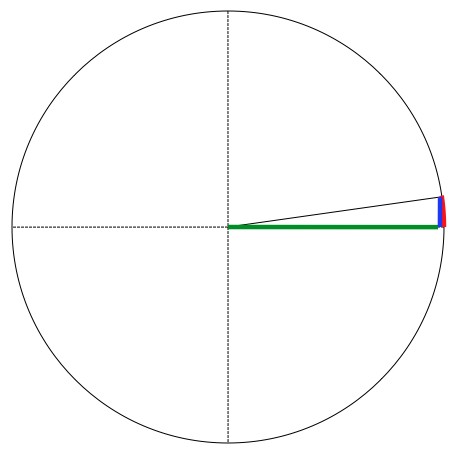
You’ll notice that when the angle is very small (and measured in radians) the value of sin(θ) and the value of θ itself become very nearly equal. Not too surprisingly, this is called the “small angle approximation” and it’s remarkably useful.
For small angles sin(θ)≈θ, but only when that angle is described in radians.
So for small values sin(θ)≈θ or 
In fact, in the limit as the angle approaches zero they are equal, or in mathspeak: 
![\frac{d}{dx}\left[\sin(x)\right] = \cos(x)](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft%5B%5Csin%28x%29%5Cright%5D+%3D+%5Ccos%28x%29&bg=ffffff&fg=000000&s=0 "\frac{d}{dx}\left[\sin(x)\right] = \cos(x)")
The derivative of a function is 
![\begin{array}{ll} \frac{d}{dx}\left[\sin(x)\right]\\[2mm] = \lim_{h\to0} \frac{\sin(x+h)-\sin(x)}{h}\\[2mm] = \lim_{h\to0} \frac{\sin(x)\cos(h)+\sin(h)\cos(x)-\sin(x)}{h} & *\\[2mm] = \lim_{h\to0} \frac{\sin(x)\left(\cos(h)-1\right)+\sin(h)\cos(x)}{h} \\[2mm] = \lim_{h\to0} \frac{\cos(h)-1}{h}\sin(x)+\frac{\sin(h)}{h}\cos(x) \\[2mm] = \lim_{h\to0} \left[-\sin(h)\frac{\sin(h)}{h} \frac{1}{\cos(h)+1}\right]\sin(x)+\frac{\sin(h)}{h}\cos(x) & ** \\[2mm] = \left[-0\cdot 1 \cdot \frac{1}{1+1}\right]\sin(x)+\cos(x) \\[2mm] =\cos(x) \end{array}](http://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D++++%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft%5B%5Csin%28x%29%5Cright%5D%5C%5C%5B2mm%5D++++%3D+%5Clim_%7Bh%5Cto0%7D+%5Cfrac%7B%5Csin%28x%2Bh%29-%5Csin%28x%29%7D%7Bh%7D%5C%5C%5B2mm%5D++++%3D+%5Clim_%7Bh%5Cto0%7D+%5Cfrac%7B%5Csin%28x%29%5Ccos%28h%29%2B%5Csin%28h%29%5Ccos%28x%29-%5Csin%28x%29%7D%7Bh%7D+%26+%2A%5C%5C%5B2mm%5D++++%3D+%5Clim_%7Bh%5Cto0%7D+%5Cfrac%7B%5Csin%28x%29%5Cleft%28%5Ccos%28h%29-1%5Cright%29%2B%5Csin%28h%29%5Ccos%28x%29%7D%7Bh%7D+%5C%5C%5B2mm%5D++++%3D+%5Clim_%7Bh%5Cto0%7D+%5Cfrac%7B%5Ccos%28h%29-1%7D%7Bh%7D%5Csin%28x%29%2B%5Cfrac%7B%5Csin%28h%29%7D%7Bh%7D%5Ccos%28x%29+%5C%5C%5B2mm%5D++++%3D+%5Clim_%7Bh%5Cto0%7D+%5Cleft%5B-%5Csin%28h%29%5Cfrac%7B%5Csin%28h%29%7D%7Bh%7D+%5Cfrac%7B1%7D%7B%5Ccos%28h%29%2B1%7D%5Cright%5D%5Csin%28x%29%2B%5Cfrac%7B%5Csin%28h%29%7D%7Bh%7D%5Ccos%28x%29+%26+%2A%2A+%5C%5C%5B2mm%5D++++%3D+%5Cleft%5B-0%5Ccdot+1+%5Ccdot+%5Cfrac%7B1%7D%7B1%2B1%7D%5Cright%5D%5Csin%28x%29%2B%5Ccos%28x%29+%5C%5C%5B2mm%5D++++%3D%5Ccos%28x%29++++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0 "\begin{array}{ll} \frac{d}{dx}\left[\sin(x)\right]\\[2mm] = \lim_{h\to0} \frac{\sin(x+h)-\sin(x)}{h}\\[2mm] = \lim_{h\to0} \frac{\sin(x)\cos(h)+\sin(h)\cos(x)-\sin(x)}{h} & *\\[2mm] = \lim_{h\to0} \frac{\sin(x)\left(\cos(h)-1\right)+\sin(h)\cos(x)}{h} \\[2mm] = \lim_{h\to0} \frac{\cos(h)-1}{h}\sin(x)+\frac{\sin(h)}{h}\cos(x) \\[2mm] = \lim_{h\to0} \left[-\sin(h)\frac{\sin(h)}{h} \frac{1}{\cos(h)+1}\right]\sin(x)+\frac{\sin(h)}{h}\cos(x) & ** \\[2mm] = \left[-0\cdot 1 \cdot \frac{1}{1+1}\right]\sin(x)+\cos(x) \\[2mm] =\cos(x) \end{array}")
That doesn’t look like a big deal, but keep in mind that all of trigonometry is just a rehashing of sine. For example, 
If it weren’t for the fact that (when using radians) 
It’s not the end of the world if you try to do calculus with degrees (it’s close), it’s just that the result is multiplied by an inconvenient constant. For example, if you’re using degrees: ![\frac{d}{dx}\left[\sin(x)\right] = \frac{\pi}{180}\cos(x)](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft%5B%5Csin%28x%29%5Cright%5D+%3D+%5Cfrac%7B%5Cpi%7D%7B180%7D%5Ccos%28x%29&bg=ffffff&fg=000000&s=0 "\frac{d}{dx}\left[\sin(x)\right] = \frac{\pi}{180}\cos(x)")
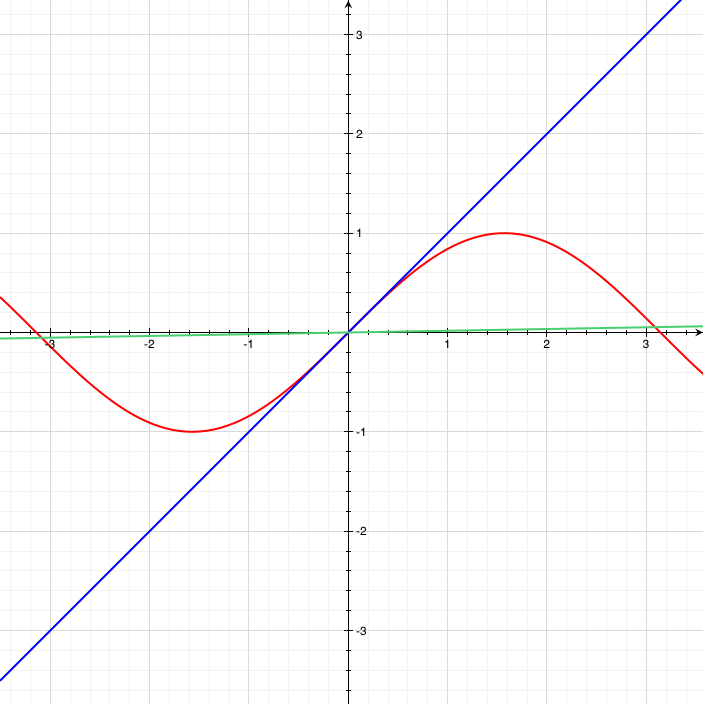
x, sin(x) in radians, and sin(x) in degrees. Notice that when measured in radians sin(x)≈x for small x, and when using degrees sine is really stretched out.
Clearly when using degrees the slope (derivative) of sine at zero is not 1, it’s much smaller (it’s 2π/360 in fact). If you don’t want any weird extra constants, then you need to use radians. But if you don’t mind them, then you be you. You can certainly use degrees or whatever, but you need to be careful with all those extra 2π/360’s.
* This is a trigonometric identity.
** That isn’t obvious:
![\begin{array}{ll} \frac{\cos(h)-1}{h} \\[2mm] = \frac{\cos(h)-1}{h}\frac{\cos(h)+1}{\cos(h)+1} \\[2mm] = \frac{\left(\cos^2(h)-1\right)}{h\left(\cos(h)+1\right)} \\[2mm] = \frac{-\sin^2(h)}{h\left(\cos(h)+1\right)} \\[2mm] = -\sin(h)\frac{\sin(h)}{h} \frac{1}{\cos(h)+1} \\[2mm] \end{array}](http://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D++++%5Cfrac%7B%5Ccos%28h%29-1%7D%7Bh%7D+%5C%5C%5B2mm%5D++++%3D+%5Cfrac%7B%5Ccos%28h%29-1%7D%7Bh%7D%5Cfrac%7B%5Ccos%28h%29%2B1%7D%7B%5Ccos%28h%29%2B1%7D+%5C%5C%5B2mm%5D++++%3D+%5Cfrac%7B%5Cleft%28%5Ccos%5E2%28h%29-1%5Cright%29%7D%7Bh%5Cleft%28%5Ccos%28h%29%2B1%5Cright%29%7D+%5C%5C%5B2mm%5D++++%3D+%5Cfrac%7B-%5Csin%5E2%28h%29%7D%7Bh%5Cleft%28%5Ccos%28h%29%2B1%5Cright%29%7D+%5C%5C%5B2mm%5D++++%3D+-%5Csin%28h%29%5Cfrac%7B%5Csin%28h%29%7D%7Bh%7D+%5Cfrac%7B1%7D%7B%5Ccos%28h%29%2B1%7D+%5C%5C%5B2mm%5D++++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0 "\begin{array}{ll} \frac{\cos(h)-1}{h} \\[2mm] = \frac{\cos(h)-1}{h}\frac{\cos(h)+1}{\cos(h)+1} \\[2mm] = \frac{\left(\cos^2(h)-1\right)}{h\left(\cos(h)+1\right)} \\[2mm] = \frac{-\sin^2(h)}{h\left(\cos(h)+1\right)} \\[2mm] = -\sin(h)\frac{\sin(h)}{h} \frac{1}{\cos(h)+1} \\[2mm] \end{array}")
I just had to comment on this. In High School (1961) my first teacher taught the study of trigons. I loved it and made all A’s. Second half semester the main teacher came back and taught “identities”. No mention of the unit circle or why you would use the unit circle. Made all F’s and was clueless. When I taught Trig as a graduate student I made sure BOTH views were taught and why electrical engineers liked the unit circle while the Forestry students loved trigons.
*Really* useful – thank you so much!
Why radians? I understand that the first commentator tried to explain but most probably lost you in the first paragraph if not sooner.
Radians connect algebra to trigonometry to geometry like nothing else can.
One radian measures the angle when the radius of a circle is traced out on its edge. Radians relate right back to Pi. (3.14………….)
There are a lot of things about this relationship that aren’t apparent at first.
The first thing to look at to get a closer view of this is a math object called the “Spiral of Squares”
This spiral is easy to construct but it reveals some relationships that are very hard to explain. For instance when you begin this spiral and measure the distance between the coils you start out with a measurement that is very close to Pi. The further out you go on this spiral the closer this measurement gets to Pi.
The next one is just as, if not more mysterious than the first. When you measure the angles between the whole number intervals on the spiral you will find that the angles between them approach 2 Pi radians.
Radians are not only convenient, in some cases they are the only correct choice.
Let me give you an example. We were told at school that the value of pi was first
approximated by drawing a regular polygon inscribed in a circle and dividing its perimeter by the radius. The more sides this polygon had, the closer to pi this value was.
So when the number of sides tends towards infinity, the perimeter of the polygon tends towards that of the circle.
here are the calculations:
let the natural number n denote the number of sides of the polygon and the positive real number r the radius of the circle (angles are taken in radians) the perimeter of the polygon is then given by the formula :
p = 2nr * sin(pi/n).
Let’s then find the limit of p as n approches positive infinity (to resolve the indeterminate form, we define N as 1/n and we use the definition of derivatives.)
Depending on the unit we use, the limit l we find is different:
When using radians we get: l = 2r*pi which is a basic geometry rule, but when we use degrees the result is totally different (360r).
I can’t really explain why this problem isn’t unit agnostic as I first thought, though.
IGNORE THE ABOVE STATEMENT. You get 2r*pi in both cases. I got them wrong because when I used degrees I omitted multiplying by pi/180. this formula is indeed unit-agnostic.
Beautifully written piece. I especially like many of your comments in parentheses. My only suggestion would be that you consider increasing font size on the equations – that font size in fractions is beginning to seem smaller 🙂 and I do slowly verify as I read.
I came to this question considering trigonometry for a population of non-STEM majors. You make excellent points and I’m not a person who would want those additional constants although somehow the 180 seems less acceptable than pi – is this esthetics?
My sense is that random collection of college graduate subway riders would struggle with correctly describing what a radian is a year after taking math but they may be able to talk a bit about degrees. I wonder if I should consider the idea six pizza slices and a tiny extra piece?
Thanks.
Because *of* calculus. We need to give grammatically incorrect Internet memes a quick and very painful death. Let’s not perpetuate them any longer.
So prescription. Much wrong.
A good way to think about it is: radians are the natural/”true” unit of angle measurement, and “degrees” and the degree symbol (°) mean nothing more and nothing less than “multiplied by π/180”.
We need to distinguish between “geometric” trigonometric functions (where the argument is an angle) and “mathematical” trigonometric functions (where the argument is a number). Let’s use an initial capital for the former (following a suggestion by Ken Brownstein). Then, for example, if theta is an angle (dimension: A) and s is a number (dimension: 1):
Sin(theta) = sin(s) = sin(theta/rad)
In other words, theta/rad is the numerical value of theta when theta is expressed in radians. The number s (= theta/rad) is the arc “length” of the unit circle corresponding to the central angle theta.
The so-called “small-angle” formula is, for the mathematical sine function:
sin(s) => s when s is a small number (very much less than 1)
For the geometrical Sine function, the formula is:
Sin(theta) => theta/rad when theta is a small angle (very much less than one radian)
Note the dimensional consistency. The left-hand side is the ratio of two lengths of the sides of a right-angled triangle; thus dim(LHS) =L/L = 1. The right-hand side is the ratio of two angles; thus dim(RHS) = A/A = 1.
For mathematical trigonometric functions, we have:
d[sin(s)]/ds = cos(s)
The corresponding formula for geometric trigonometric functions is:
d[Sin(theta)]/d(theta) = Cos(theta)/rad
Again, note the dimensional consistency: dim(LHS) = 1/A; dim(RHS) = 1/A. [Note that this “explains” the appearance of “pi/180”–since rad = 180/pi deg.]
Euclid’s Elements (Book VI, Proposition 33) states that, in the same circle (or two equal circles), the ratio of two arc lengths is in the same proportion as the ratio of the corresponding central angles:
s1/s2 = theta1/theta2
If we let s1 = s be any arc length and theta1 = theta the corresponding central angle, then set s2 = c, the circumference, for which theta2 = rev (one revolution), we have:
s/theta = c/rev
[This is true in some non-Eucldian geometries, as well.] In plane (Euclidean) geometry, c = 2 pi R; so we have:
s/theta = R/[rev/(2 pi)] = R/rad
where rad is DEFINED as rad = rev/(2 pi). The formula relating circular arc-length, s, radius, R, and central angle, theta, is thus:
s = R theta/rad
Dimensional consistency: dim(LHS) = L; dim(RHS) = L A/A = L. In this correct formula, ANY angle units can be used for theta! In this formula, rad is a “reference angle denominator” that arises naturally from Euclid’s proposition. Since it has dimension A (and crops up so often), it is a good CHOICE as a unit for angle.
Doesn’t the degree also approach zero when sin(degree) is also approaching zero?
Why is this fact exclusive to radians, this isn’t obvious to me.
Thanks.
@Saud
Absolutely! As (degree) approaches zero, sin(degree) approaches zero, but they do so at very different rates. With radians as (radian) approaches, sin(radian) approaches zero and (radian) and sin(radian) are approximately equal to each other. So a given change in one means about the same change in the other.
Great discussion, but feels like you set up a straw man argument by saying radians are better than degrees. What about turns?
sin(t)=2pi cos(t)
and
the limit as t goes to 0 of sin(t)/t is 2pi
I see no problem with 2 pi showing up in circular functions
(It’s even better if you rewrite 2pi as tau!)
I’ve always wondered what alien civilizations would think about these types of choices that we make. I’ve never been a fan of radians (or pi, or the imperial system, the list goes on…)
This could just be me personally and how my mind works, but I never got the sin/cos/tan or what it should be used for, hardly even managed to memorize it for a couple of years in school, and then later, we were taught the unit circle and it all clicked into place, because there was a *reason*.
I guess teachers know what they are doing, but since then I’ve always wondered if it could be taught like that from the start, you know, to show *why* sin/cos/tan etc are what they are.
As an electrical engineer, I find radian measure either a pain or pretty useless.
Who says AC power has a frequency of 314.159 radians/second in Europe, but
in the US it’s 377 radians/second ? Or a ship’s captain going to the south pole
ordering the helmsman to bearing 3.14159 radians ? Except for snipers, when
you leave your ivory tower it’s degrees. My $10 Casio calculator defaults to
degrees and sin(30)=0.5 not 0.4999999999… but for 70 years programmers
have been telling us their big expensive computers just can’t handle degrees.
Quit whining and making excuses. Just do your job, if takes triple or quadruple
precision calculations so be it. Computers are here to make our lives easier.
It’s like the old RPN and stack machine argument. Who cares about using
registers more efficiently when you can put millions of them on one IC ?
Nerds.
Pingback: How to Easily Convert Degrees to Radians (and Radians to Degrees) - Gur Times
Pingback: How to Easily Convert Degrees to Radians (and Radians to Degrees) - Your Lifestyle Magazine