Physicist: One of the most profound insights ever made by peoplekind is that time is relative. This isn’t some abstract idea, mistake, or mathematical artifact. If you have two identically functioning clocks, you can start them together, move them to different locations or along different paths, then when you physically bring them back together to compare, they will literally have registered different amounts of time.
You may be inclined to say, “sure, it’s weird… but which clock is right?”. The existentially terrifying answer is: there is no such thing as a “correct clock”. Every clock measures its own time and there is no such thing as a universal time. And yet, cosmologists are always talking about the age of the universe (a mere 13.80±0.02 billion years young). When talking about the age of the universe we’re talking about the age of everything in it. But how can we possibly talk about the age of the universe if everything in it has its own personal time?
The short answer is: almost everything is about the same age. The biggest time discrepancy is between things deep inside of galaxies and things well outside of galaxies, amounting to a couple parts per million (or one or two seconds per week). Matter that has been in the middle of large galaxies since early in the universe’s history should be no more than on the order of 50,000 years younger than matter that has managed to remain in intergalactic space. Considering that our best estimates for the age of the universe are only accurate to within 20 million years or so (0.1% relative error), a few dozen millennia here and there doesn’t make any difference.
There are two ways to get clocks to disagree: the twin paradox and gravitational time dilation. The twin paradox a bizarre consequence of the difference between ordinary geometry and spacetime geometry. In ordinary geometry, the shortest distance between two points is a straight line. In spacetime geometry, the longest time between two points is a straight line. A “straight line” in spacetime includes sitting still, so if you start with two clocks in the same place and take one on a trip that eventually brings it back to its stationary partner, then the traveling clock will have fallen behind its sedentary twin.
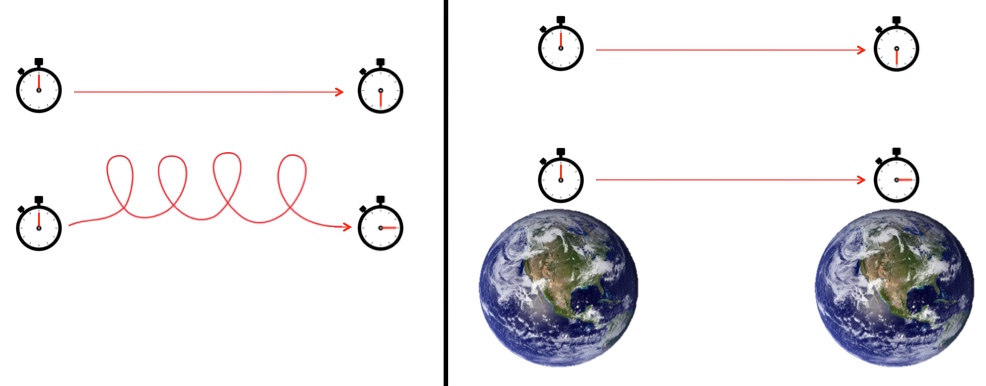
The Twin Paradox: The straighter the path taken between two locations, the more time is experienced. Gravitational Time Dilation: Things farther from mass experience more time.
Assuming that the traveling clock travels at a more-or-less constant speed, you can figure out how much less time it experiences pretty easily. If the traveling clock experiences 
Gravitational time dilation is caused by the warping of spacetime caused by the presence of energy and matter (mostly matter) which is a shockingly difficult thing to figure out. When Einstein initially wrote down the equations that describe the relationship between mass/energy and spacetime he didn’t really expect them to be solved (other than the trivial empty-space solution); it took Schwarzschild to figure out the shape of spacetime around spherical objects (which is useful, considering how much round stuff there is to be found in space). He did such a good job that the event horizon of a black hole, the boundary beyond which nothing escapes, is known in fancy science circles as the “schwarzschild radius”.
Fortunately, for reasonable situations (not-black-hole situations), you can calculate the time dilation between different altitudes by figuring out how fast a thing would be falling if it made the trip from the top height to the bottom height. Once you’ve got that speed, v, you plug it into 
By and large, the effect from the twin paradox is smaller than the effect from gravity, because if something is traveling faster than the local escape velocity, then it escapes. So the velocity you plug into gamma for the twin paradox (the physical velocity) is lower than the velocity you’d plug in for gravitational dilation (the escape velocity). If you have some stars swirling about in a galaxy, then you can be pretty sure that they’re moving well below the escape velocity.
The escape velocity from the surface of the Earth is 11km/s, which yields a gamma of 
Point is, it doesn’t make too much difference where you are in the universe: time is time.
Now admittedly, there are examples of things either trapped in black holes or screaming across the universe at near the speed of light, but the good news for us (on both counts) is that such stuff is rare. The only things that move anywhere close to the speed of light is light itself (no surprise) and occasionally individual particles of matter. Light literally experiences zero time, so the “oldest” photons are still newborns; they have a very different notion of how old the universe is. No one is entirely sure how much of the matter in the universe is presently tied up in black holes, but it’s generally assumed to be a small fraction of the total.
Long story short: when someone says that the universe is 13.8 billion years old, they’re talking about the age of the matter in the universe, almost all of which is effectively the same age.
A muon whirling around a storage ring has a big time dilation. Indeed the time it takes them to decay is much longer and w/o this effect they wouldn’t live long enough to be stored
Thank you very much for this, a very clear explanation!
An excellent explanation. I can only add that the universal time is measured with reference to the Hubble Parameter (H). The surface along which H has the same value is considered to be a surface of the same universal time. In other words, the state of expansion of the universe determines the universal time.
You discussed how the clock traveling as constant speed experiences time, but the reciprocal is also true. That clock can be considered stationary and the “at rest” clock moving away, so they both experience the longer time.
It was also discussed that the preponderance of mass in the universe has little relative motion so all experiences similar time approximated by the age of the universe. Isn’t it still legitimate to do the thought experiment of traveling with a neutrino and find a very different passage of time and a different age? It gets hard to wrap your head around.
About the photon experiencing the null interval, is it always at the beginning of time, or is it always current at what we consider present time. Or is it at all times always??
@Douglas Franks
That’s why it’s important to stipulate that the clocks start together and end together. Otherwise, the rate of time is (as you point out) subjective. However, the straight-line vs. curved-path thing is objective and does lead to different results.
Things that travel near the speed of light (relative to some frame) between two locations/events (defined by that same frame) will experience less time on the journey than things that are stationary (in that same frame). A photon traveling from here to the Moon will take about a second according to us, but zero time according to the photon. It turns out that asking “what is the photon’s point of view” is remarkably fruitless; if a photon doesn’t physically run into something, then that thing may as well not exist. While we material beings can talk about coordinates and time and travel, photons don’t. Not really.
High speed things have a very different perspective on the universe, no more or less valid than any other, but I figured it would be more useful to consider what the vast majority of the matter in the universe sees when it considers the vast majority of the matter in the universe.
To get the twin paradox one twin must accelerate differently than the other. If they are riding in ‘elevators’ they experience different ‘gravitational’ fields and the effect is not different from going near a black hole (but not too near!) and coming back out to meet up again.
@Traruh Synred
It’s subtle, but although there must be acceleration for a curved path, acceleration is not the cause of the twin paradox. The top diagram here is a decent explanation of why.
We’ll that’s interesting.
I remember doing a calculation (homework, I think) as an undergrad. counting ‘heart beats’ and it seemed the acceleration was critical (It was taken to be infinite, so we’d only need special relativity). There has to be some acceleration to break the symmetry, but I guess it can be anything. But indeed the difference in twin age depended on how far/long and the speed of the traveling twin.
The approaching black hole equivalence is wrong apparently.
Will a clock at the bottom of an upward accelerating elevator run differently than one at the top? Seems like it must by the equivalence principle… for a ridged elevator the clocks would always be at the same speed.
What happens if the elevator stops?
If infinity is a solid, the momements of the two clocks relative to infinity are different.
If time is momement relative to the solid of infinity, of course, to each other they would
be different.
It was stated that all of the matter in the universe has little variation in frame of reference, and therefore similar time.
I have understood that out at the visual horizon of our universe galaxies are moving away from us at close to the speed of light caused by be some high bred of the expansion of space and conventional motion. If there are such high speed differentials would there not also be significant differentials in time for large structures in the universe?
@Douglas Franks
Expansion of space is not the same thing as movement for relativistic purposes.
Let’s call a photon, “A”. A is outside time. “A” also crosses the event horizon of a black hole. What time did it cross that line? Did it enter a specific time when it crossed? Could it ever cross over? If so when did A cross the event horizon?
We can estimate the age of the universe, as you say, with an approximate universal time. But incidentally, wouldn’t matter moving at just below c, such as neutrinos, get further out of sync with other matter over 12 bn yrs (give them a bit of time before they get emitted), than 50,000 years? If they travel at 0.999976 c then they’re time dilated by a factor of 144, which gets them out of sync with other matter by 83 million years.
@David
Sure, but neutrinos are nearly impossible to detect as-is. So very little is known about them, IIRC we only recently figured out that they can ‘oscillate’ into different kinds (flavors I think?) of neutrinos which are even harder to detect than the normal kind.
I have no clue if we can date neutrinos. They are a very, very strange particle.
Hi, I have done a blog on an experiment that I did in freshmen year of school, relating to the refractive index. Please feel free to check it out and leave feedback. Thank you.
Why does the energy of stone is increase when we throw at high speed?
Work = Force x distance (Work means energy imparted to object worked on). I.e., it’s caused by throwing the rock.
In another comment it was stated that a photon may as well not exist until it hits something, interacts with matter. Being timeless, when a photon from the Sun hits the Earth, in its frame, that is also the instance that it left the Sun. That is difficult intuitively, that it left the Sun and hit the Earth at the same instance. While in our frame there was time.
What will happen to our body if we traveled with equivalent speed of light on space?
Will body get more energy or destroyed?
Explain me briefly?
>What will happen to our body if we traveled with equivalent speed of light on space?
Don’t worry, you can’t get to the speed of light.
If you get close the gas and plasma in space will look like radiation. You might get radiation sickness and die, if you don’t hit a speck of dust that likely would kill you out right.
However, the energy needed to get that close to c is not available, so there’s nothing to worry about even for this more modest speed. There are enough real disasters to worry about.
Why does time dilation occurs while travelling at speed of light?
@Ramesh I
There’s a post here that may answer your question.
What is the difference between gravity and gravitational waves?
Einstein realized that the one way speed of light is a convention that we must choose, so he chose it to be the same in both directions to make the math easier, but that was the only reason. And using that convention, very distant stars will need billions of years for the light to travel to Earth. But you can choose the speed of light to be instantaneous moving towards you and ½ c moving away from you and it is just as valid as the convention that Einstein chose. And light from across the galaxy will arrive on Earth instantaneously.
https://answersingenesis.org/astronomy/starlight/distant-starlight-thesis/
“. . . if only I knew that the light by means of which the observer at M perceives the lightning flashes travels along the length A → M with the same velocity as along the length B → M. But an examination would only be possible if we already had at our disposal the means of measuring time. It would thus appear as though we were moving here in a logical circle.” (Einstein 1961, pp. 22–23).
@Jonathan Cook
That quote is out of context. Here’s the entire book. That quote appears on page 18 (page 30 of the pdf) and it is a hypothetical conversation in which Einstein imagines someone else attacking his ideas about simultaneity. It is not about the “one way speed of light” and it is not something that Einstein is actually advocating.
The universality of the speed of light is something that can and has been experimentally verified. In fact, the first roughly accurate measurement of the speed of light was a “one-way” measurement done in 1676. The Moons of Jupiter eclipse behind it in a very predictable way, that varies as the distance between Jupiter and Earth changes throughout their orbits. This change in time is exactly proportional to the change in distance, and is due to the time it takes for light to get from there to here. This effect needs to be taken into account every time we look at anything else in the solar system (as needed). If the speed of light were different in different directions, then (just looking at this one experiment) we’d need to re-write our understanding of gravity to explain how the moons of Jupiter speed up and slow down, and especially how they manage to take into account the constantly changing relative positions of Earth and Jupiter (the “fast and slow directions” would point in different directions every year). This same experiment can be done with the moons of Mars, Saturn, Uranus, and Neptune, producing the same consistent speed of light, at the same time, regardless of where they are with respect to Earth.
It is possible to construct a framework for physics in which the “two-way” and “one-way” speeds are different, but those constructions also involve making up new dynamics to explain why clocks of all kinds (including orbiting Moons) always know that they’re being moved and somehow adjust themselves. In order for these theories to be consistent with observation and experiment, they need to be exactly equivalent to a pointlessly weird choice of coordinates. It would be like walking across a room with the international dateline running down the middle and claiming that you must have been walking very slowly (despite all direct observations to the contrary), because it took a full day to make the trip.
Technically the invariance of light speed with respect to direction is a convention to make the math easier, but then again you really have to go out of your way to make the math harder.
Is time dilation the reason the speed of light is the same for everyone? In other words, say I was watching “A” moving Across the sky at c (I know it can’t, butt….) and “B” chasing it at .95c, then id see A moving away from B at .5c. But B would still observe A moving away at c. Would this would be because by the time B’s clock ticked an hour, A would be 68o+ billion miles further away? Is that right or am I way off base here?
@The Physicist That is not correct. The one way speed of light cannot be measured even in theory. You must choose an arbitrary synchronization convention. https://en.m.wikipedia.org/wiki/One-way_speed_of_light
Man I wish I could understand this information. I’m always asking myself questions about the universe, but the answers go right over my head.
In twin paradox you leave out (at least explicitly) that motion is relative. That from the point of view of the traveling twin the time of his stay at home brother is also slowed.
As undergrad I once worked this out in detail as is seemed so ‘paradoxical’ to me, including of course that the traveler had to turn around to bet back and compare clocks. Not sure I could still do it though it is only high school algebra.
Surely the idea that photons don’t experience time is relative. If I travelled away from stationary you at light speed, then to you, I would not experience time. But in my new frame of reference I would age at the same rate as I did in my old frame of reference or am I missing something obvious.
Your right. It’s a common missundertanding that your time changes. It does not. Only time relative to others frames and trajectories changes. You don’t live any longer.
It does seem to me that the idea that we have to bring the ‘twins’ back together to observe time difference is wrong.
It we send a muon down a beam line to a bubble chamber and stop it in there, it will not have decayed. It will shortly after stopping.
Though it will have only lasted it usual lifetime it’s own frame, it will have lived long enough to get down the beam line to to the chamber. If we compare the time ad on the chamber clock to that back at the start of the muons travels, it will show a difference corresponding to time it took the muon to transit the beam line and the muon will in the lab frame be much ‘older’ than it is in it’s own frame. I muon created at near rest in the chamber at the same time the beam line muon was launched on its way will be long decayed away.
There’s no need to bring it back to it’s point of origin to get twin ‘paradox’.
Indeed this illustrates the lack of need for any acceleration (which I ‘d used to think that was important).
If the beam line muon merely has it time of arrival at the chamber measured, it will still have outlived any non-moving counter parts created when it started down the beam line.
Otherwise experiments with muon beams would never work!
Describing it from the beam line muons point of view is more complicated, but involves the lab clock (mouns) not starting at the same time in that frame.
is it not also the case that as mass cannot travel at light speed there is a limit to how far into the future one could travel in our reference frame. If I travel away from you at a speed which causes time dilation to occur and I go so far and then return. I would meet you again and your age will have increased more than mine but I cannot return to a point where your universe has ended as I was travelling in the same universe so surely there must be physics that disallow extreme time dilation. Surely some effect must be reversed during the return journey to prevent such an outcome. Maybe it’s our method of measuring the concept we call time that is ultimately flawed
I don’t think there’s any flaw in how we measure time. All this has been confirrmed in colliders and fixed target experiments.
Physics is descriptive not prescriptive. It’s just the way charged particles behave and indeed defines what in means to be a charged, i.e., to produce electric fields that attract or repel other charged particles depending on what charge they have.
The thought remains. The closer you travel to light speed the more extreme the time dilation, the effect is exponential. So how far in theory could one person travel into ‘the future’ of another person? Are there physics equations that would show that if you travelled at speed x for y time and then returned then the sun and earth would no longer be there? for example.
Indeed possible. Nothing wrong with that.
If you go near a black hole and come back out you may find everybody gone too. Don’t think we have experiment for that yet and might not want it.
Time dilation is proportional to 1/gamma
where gamma=1/sqrt(1-v^2/c^2). That not exponential. Indeed it rather slow.
Thanks for your responses Arthur. Your knowledge of Maths and Physics is greater than mine and I’m sure the equation you entered is correct but for any v smaller than c would result in trying to find the square root of a negative. I’m probably missing something obvious. Another thought I still have (leaving aside possible destructions at black holes etc). If you travelled at 99.99% light speed and travelled for half your lifespan (as you would need the other half to travel back). Is it the case that when you returned to the starting point, the universe would still exist? A long long time may have passed relative to your starting position but not the lifespan of the universe. Is this true according to current cosmological theory?
Is the equation not
t = tzero/sqrt(1-(vsquared/csquared))
Brackets in equations assist understanding. I thought there would be a negative within the square root portion as I assumed 1-v^2/c^2 meant 1-v^2 on the top line and c^2 on the bottom line. Playing a little with the formula t=tzero/sqrt(1-(v^2/c^2)) where tzero is the time experienced by the travellers frame of reference. As I said I am not highly qualified in Maths. I am a retired teacher with an old degree in Computer Science.
The important value for the tzero divisor seems to be 3162277 with as many zeros in front of it as you like depending on how close you want v to be to c.
So if tzero was say 50 and the divisor was 0.3162277 x 10 ^ -50 then the time t passed at the start point would be 158 x 10^51.
Surely this is bigger than the lifespan of the universe.
So the question remains
How can your return to a point in a universe that has ended due to travelling through that same universe at very close to light speed for 50 relative years.
I know my approach here is very simplistic
My maths is probably wrong.
I assume the 50 years travelling time is 25 out and 25 back.
I look forward to being shot down in flames here as I want the time dilation equations to be correct so please, all you clever people out there, shoot me down!
Seems like second time I’ve rec’d this. It’s still non-sense.
Thanks for your detailed description of why you think it’s nonesense.
I’m sure the academic world marvels at your depth of knowledge and your powers of description. Perhaps you could get a job with a good all American preacher man.
Anonymously of course.
Retired Experimentalist.
Indeed that’s what I said. I used computer style notation as you can’t write properly in plain text available.
BTW. Academia is not going to pay the least attention to either of us, and if I weren’t retired I wouldn’t be wasting my time on it at all
It’s sad you feel that way. I am quite happy to be shown as typing nonesense as I can learn from it. I love discussing any aspect of cosmology. I think interested people can benefit greatly from any scientist (retired or active) with the humility and understanding required to be a good educator. I am grateful to such people when they aid in progressing my understanding. I appreciate it may be frustrating for the Sheldon Cooper type scientists with social difficulties to be tolerant of those who are not as knowledgeable as they are but I think Science will gain more followers due to those scientists who are also good educators. The ivory towered arrogant scientist is more likely to chase people over to the God Squad. My previous posts remain only partially answered. If you can’t explain the errors in my thinking Arthur then I appreciate your attempts so far but if you find the effort beyond your tolerances then you shoul leave it to others. I will hopefully be sated by other sources if this forum proves fruitless.
I hope you had a wonderful career in experimental research. Retirement does not stop you being a powerful scientific force with a great deal to offer lay people. Your reward is the gratitude of your potential learners. As a teacher of 30 years before I retired, believe me, there is no greater currency.
I sent my question to Ask an Astronomer and got the answer pasted below. A pleasant and useful answers which might demonstrate to some others the correct way to communicate with others on forums such as this.
Great question. Relativity is…weird. In essence you’re right that as an object’s
velocity approaches the speed of light, time dilation becomes more and more
extreme, so theoretically B could travel fast enough to ‘arrive’ at the time of the
end of the universe. Of course, this is all theoretical in that nothing with mass can
actually move at the speed of light. Lots of things happen as a result of traveling at
relativistic speeds other than just time dilation, for one thing, traveling at these
speeds takes ever increasing amounts of energy, which makes it impractical, at
least for the moment.
Interestingly, you can get some of the same weird effects from being close to a
gravitational mass–clocks on earth ‘tick’ slower than clocks on airplanes, because
the clock on the airplane is further away from the Earth’s center of mass (so the
airplane clock is like A here, the clock on the ground is like B). This is called
‘General relativity’ and describes how mass warps space-time. The type of
relativity that you’ve asked about is ‘Special’ relativity. I’ve put some links below in
case you’re interested in learning more:
http://www.astro.ucla.edu/~wright/relatvty.htm
https://imagine.gsfc.nasa.gov/ask_astro/relativity.html
https://en.wikipedia.org/wiki/Time_dilation
Thanks for your question!
-Ask an Astronomer
My question is about the beginning of the universe, at the beginning matter was more concentrated close together before expansion and wouldnt that make time pass slower… space expanded far enough away for time to pass faster.. ?