Physicist: The very short answer is: use the spherical law of cosines so you can do trigonometry on a sphere.
This is a seriously old problem that needed to be solved before we became a routinely globe-trotting species. If you have the latitude and longitude of your location and a destination, you could just move east/west until you match the destination’s longitude then move north/south until you match the latitude. But that’s a big waste of time, as the so-intuitively-obvious-it-barely-deserves-a-name “triangle inequality” will tell you.
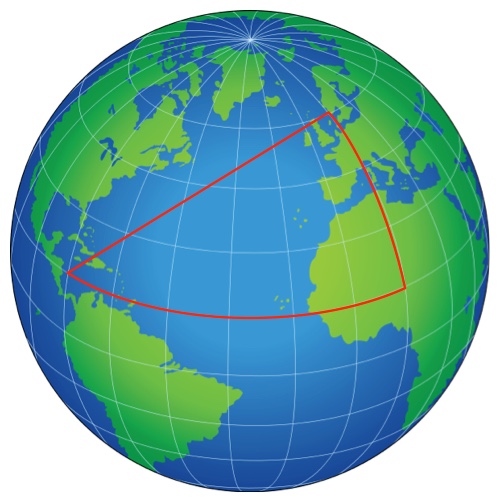
The “triangle inequality” says that the sum of any two sides of a triangle are longer than any one side. So if you’re traveling from Nicaragua to Norway, don’t go via Nigeria.
As you may have heard, the shortest distance between two points is a straight line. For curved surfaces the closest you can get to a straight line is a “geodesic”, which is a straight line on small scales, but it you step back may be going all over the place. If you wrap a ribbon around a gift (or any manner of festive package) and manage to keep it flat, you’ve found a geodesic, because if the path of the ribbon changes direction, the ribbon kinks. On a sphere like Earth, where you’re stuck moving along the surface (instead of drilling straight through like some kind of compulsive, fire-proof mole), the geodesics are “great circles”. If you walk in a straight line, you’re walking on a great circle.
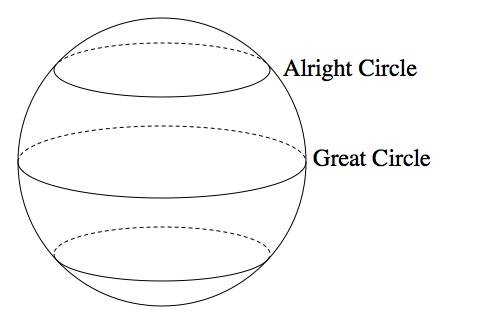
A great circle is the path you’ll follow if you walk in a straight line on a sphere. Smaller circles result from not-straight-lines (continuously turning a little to the side).
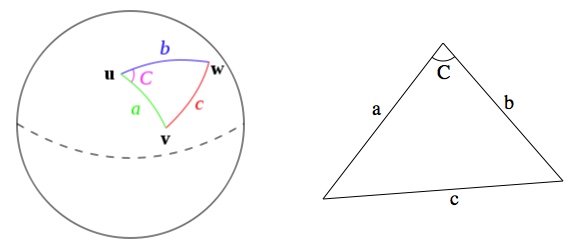
Doing geometry on a sphere is more difficult than geometry on a flat plane, but not by a hell of a lot. Geometry, despite what some pudunk Greek philosophers may say, is basically just playing with triangles. A nice, universal rule for any triangle is the Law of Cosines which relates the lengths of the three sides, a, b, and c, with the angle opposite one of those sides, C: 
Left: A triangle made from great arcs. Right: A triangle made from straight lines.
Slap that triangle on the side of a sphere and that law becomes the Spherical Law of Cosines:
Here the meaning of a, b, and c has changed a little. Lengths on a sphere can be described by angles (drawn from the center to the surface). If you’re using radians (which you always should), those angles are 
Lucky for us, positions on Earth are usually described in terms of angles (latitude and longitude) and not distances, so the spherical law of cosines is ready to go. Just put the corners at the north pole, where you’re at, and where you’re planning to go.
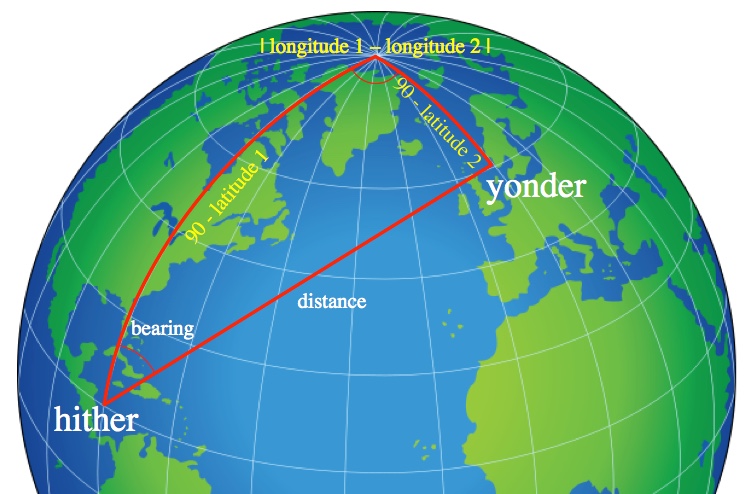
If you put the corners of the triangle at a pole, your location, and your destination, then you can read off the lengths of two sides (90-latitude) and the angle at the pole (the difference of the longitudes). From these there’s enough information to find the distance and bearing to the destination.
The law of cosines (either of them) relates four things: all three sides and one of the angles. If you have any three of those pieces of information you can solve for the forth. With the latitudes we have two sides and with the difference of the longitudes we got an angle.
First (because you always should) convert your angles from degrees to radians by multiplying by 
and therefore
![\textrm{distance}=(\textrm{Earth's radius})\arccos\left[\cos\left(\theta_1\right)\cos(\theta_2)+\sin\left(\theta_1\right)\sin(\theta_2)\cos(\phi)\right]](https://s0.wp.com/latex.php?latex=%5Ctextrm%7Bdistance%7D%3D%28%5Ctextrm%7BEarth%27s+radius%7D%29%5Carccos%5Cleft%5B%5Ccos%5Cleft%28%5Ctheta_1%5Cright%29%5Ccos%28%5Ctheta_2%29%2B%5Csin%5Cleft%28%5Ctheta_1%5Cright%29%5Csin%28%5Ctheta_2%29%5Ccos%28%5Cphi%29%5Cright%5D&bg=ffffff&fg=000000&s=0 "\textrm{distance}=(\textrm{Earth's radius})\arccos\left[\cos\left(\theta_1\right)\cos(\theta_2)+\sin\left(\theta_1\right)\sin(\theta_2)\cos(\phi)\right]")
Boom! There’s the distance. And with three sides in hand (the two given by the latitudes and the distance from, like, two seconds ago) you can find your “bearing”, the angle between north and your destination.
and so
![\textrm{bearing}=\arccos\left[\frac{\cos\left(\theta_2\right)-\cos\left(\theta_1\right)\cos\left(\frac{\textrm{distance}}{\textrm{Earth's radius}}\right)}{\sin\left(\theta_1\right)\sin\left(\frac{\textrm{distance}}{\textrm{Earth's radius}}\right)}\right]](https://s0.wp.com/latex.php?latex=%5Ctextrm%7Bbearing%7D%3D%5Carccos%5Cleft%5B%5Cfrac%7B%5Ccos%5Cleft%28%5Ctheta_2%5Cright%29-%5Ccos%5Cleft%28%5Ctheta_1%5Cright%29%5Ccos%5Cleft%28%5Cfrac%7B%5Ctextrm%7Bdistance%7D%7D%7B%5Ctextrm%7BEarth%27s+radius%7D%7D%5Cright%29%7D%7B%5Csin%5Cleft%28%5Ctheta_1%5Cright%29%5Csin%5Cleft%28%5Cfrac%7B%5Ctextrm%7Bdistance%7D%7D%7B%5Ctextrm%7BEarth%27s+radius%7D%7D%5Cright%29%7D%5Cright%5D&bg=ffffff&fg=000000&s=0 "\textrm{bearing}=\arccos\left[\frac{\cos\left(\theta_2\right)-\cos\left(\theta_1\right)\cos\left(\frac{\textrm{distance}}{\textrm{Earth's radius}}\right)}{\sin\left(\theta_1\right)\sin\left(\frac{\textrm{distance}}{\textrm{Earth's radius}}\right)}\right]")
For example, if you happen to be traveling from Nueva Guinea, Nicaragua (11.6932° N, 84.4540° W) to Nesflaten, Norway (59.6466° N, 6.7997° E), the angles involved are 
![\textrm{distance}=(3959miles)\arccos\left[\cos\left(1.367\right)\cos(0.530)+\sin\left(1.367\right)\sin(0.530)\cos(1.593)\right]=(3959miles)(1.406)=5566miles](https://s0.wp.com/latex.php?latex=%5Ctextrm%7Bdistance%7D%3D%283959miles%29%5Carccos%5Cleft%5B%5Ccos%5Cleft%281.367%5Cright%29%5Ccos%280.530%29%2B%5Csin%5Cleft%281.367%5Cright%29%5Csin%280.530%29%5Ccos%281.593%29%5Cright%5D%3D%283959miles%29%281.406%29%3D5566miles&bg=ffffff&fg=000000&s=0 "\textrm{distance}=(3959miles)\arccos\left[\cos\left(1.367\right)\cos(0.530)+\sin\left(1.367\right)\sin(0.530)\cos(1.593)\right]=(3959miles)(1.406)=5566miles")
and the bearing is
![\textrm{bearing}=\arccos\left[\frac{\cos\left(0.530\right)-\cos\left(1.367\right)\cos\left(\frac{5566}{3959}\right)}{\sin\left(1.367\right)\sin\left(\frac{5566}{3959}\right)}\right]=0.538rad=30.1^o](https://s0.wp.com/latex.php?latex=%5Ctextrm%7Bbearing%7D%3D%5Carccos%5Cleft%5B%5Cfrac%7B%5Ccos%5Cleft%280.530%5Cright%29-%5Ccos%5Cleft%281.367%5Cright%29%5Ccos%5Cleft%28%5Cfrac%7B5566%7D%7B3959%7D%5Cright%29%7D%7B%5Csin%5Cleft%281.367%5Cright%29%5Csin%5Cleft%28%5Cfrac%7B5566%7D%7B3959%7D%5Cright%29%7D%5Cright%5D%3D0.538rad%3D30.1%5Eo&bg=ffffff&fg=000000&s=0 "\textrm{bearing}=\arccos\left[\frac{\cos\left(0.530\right)-\cos\left(1.367\right)\cos\left(\frac{5566}{3959}\right)}{\sin\left(1.367\right)\sin\left(\frac{5566}{3959}\right)}\right]=0.538rad=30.1^o")
If you want to walk in a straight line from downtown Nueva Guinea to uptown Nesflaten, you’d face due north, turn about 30 degrees to the right, and walk in a straight line for about two and a half months, while ignoring the Atlantic Ocean to the best of your ability.
So how do you calculate distance and bearing? A small bucket of math. Today if you want to calculate sines and cosines you break out a computer. So you may be wondering how they did this math back in the days of sailing ships (without GPS). They didn’t. Calculating was done once, then written down, then looked up many times. Once upon a time books were useful!
A very boring book from the 17th century wherein you can look up the values of trig functions.
The people who actually did the calculating were “computers”; pitiable folk who sat in dark rooms and slowly went mad and rarely got to sail around the world.
If all you want to do is calculate the “as the bird flies” distance it is child’s play. Why not postulate how to calculate the ACTUAL travelling distances say, by car, which will not allow you to drive over water or through mountains?
Just need to apply a bit of fractal geometry!
Can’t you just stretch a thread between the points on the globe map and measure the thread length?
@Leo
Sure! Just takes a lot of string, and knowing where to take one end of that string.
Yes but you would need a real size globe and a lot of thread.
Why, you can use any globe you find in shops, just multiply your result by the globe scale.
Thank you. IF only the trig prof had started the course with this example, I could have then been interested in trig and gotten a better grade.
G
btw looking for a co author of book with math and physics background
🙂
G
Yet not once mentioning the haversine formula?
Since I never learned any spherical geometry, but have been studying 3D graphics, distance is a problem I would have solved with a dot product, and erecting a (very tall) tower at the cross product would give a great landmark for navigational purposes.
But math being what it is, I imagine all solutions to this problem are really the same solution, underneath their clothing?
The real question is this; what’s the distance between two points (on the surface of a sphere), through the sphere?