The original question was: I can’t find a consistent answer to this question; please help. A spaceship leaves Earth and heads to a star 4 light years away at 80% of light speed. An observer on Earth knows that the spaceship’s clock will run slower than his clock by 40% for the entirety of the journey (according to the Lorentz formula).
According to the Earth-based observer, the spaceship will arrive at the star in 5 years. However, because of time dilation, the spaceship’s clock will only read 3 years of elapsed time on arrival. To an astronaut on the spaceship, the distance to the star appears to be just 2.4 light years because it took him just 3 years to get there while traveling at 80% light speed.
This situation is sometimes explained as a consequence of length contraction. But what is it that’s contracting? Some authors put it down to space itself contracting, or just distance contracting (which it seems to me amounts to the same thing) and others say that’s nonsense because you could posit two spaceships heading in the same direction momentarily side by side and traveling at different speeds, so how can there be two different distances?
So what is the correct way to understand the situation from the astronaut’s perspective?
Physicist: Space and time don’t react to how you move around. They don’t contract or slow down just because you move fast relative to someone somewhere. What changes is how you perceive space and time.
There’s no true “forward” direction and, terrifyingly, there’s no true “future” direction or even “space but not time” direction. All of these directions and the lengths of things in those directions are subjective and even, dare I say, relative.
When you measure the length of something in space (in other words, “normally”), the total length isn’t just the length in the x or y directions, it’s a particular combination of both that works out exactly the way you’d think it should. When you measure the length of something in spacetime, the total length isn’t just the length in the space or time directions, it’s a particular combination of both that works out in more or less the opposite of how you’d think it should.
We don’t talk about the three dimensions of space individually, because they’re not really distinct. The forward, right, and up directions are a good way to describe the three different dimensions of space, but of course they vary from perspective to perspective. Just call someone from the opposite side of the planet and ask them “What’s up?” and you’ll find yourself instantly embroiled in irreconcilable conflict. Everyone can agree that it’s easy to pick three mutually perpendicular directions in our three-dimensional universe (try it), but there’s no sense in trying to specify which specific three are the “true” directions.
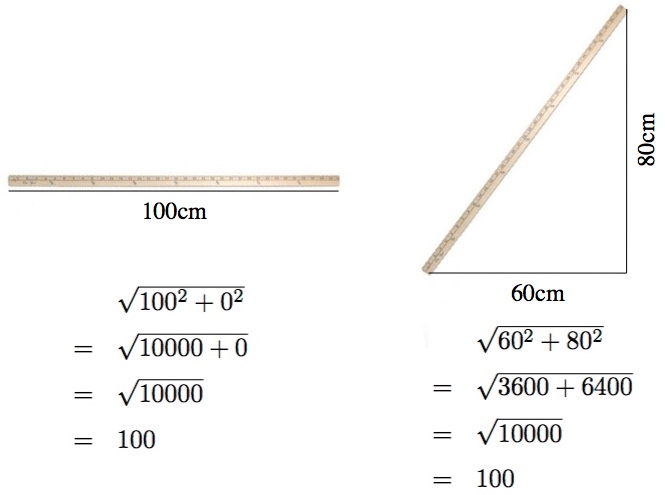
If you insist on measuring things in only one direction, then different perspectives will result in different lengths. To find the total length, d, requires doing a couple measurements, x and y (and z too, in 3 dimensions), and applying some Pythagoras, d2=x2+y2.
A meter stick is a meter long (hence the name), so if you place it flat on a table and measure its horizontal length (with a… tape measure or something), you’ll find that its horizontal length is 100cm and its vertical length is zero. Given that, you could reasonably divine that it must be 100cm long. But if you tilt it up (or equivalently, tilt your head a bit), then the horizontal and vertical lengths change. There’s nothing profound happening. To handle a universe cruel enough to allow such differing perspectives we use the “Euclidean metric”, 
Einstein’s big contribution (or one of them at least) was “combining” time and space under the umbrella of “spacetime”, so named because Germans love sticking words together in a traditional process called (roughly translated) stickingwordstogethertomakeonereallylongdifficulttoreadandoftunpronounceableword.
The different spatial dimensions are equivalent. To see for yourself, walk north and south, then walk east and west. Unless you’re carrying a compass, you shouldn’t notice any difference. But clearly time is different. To see for yourself, first walk north and south, then walk to tomorrow and back to yesterday. So when someone cleverly volunteers “we live in a 4 dimensional universe!”, they’re being a little imprecise. Physicists, who love precision slightly more than being understood, prefer to say “we live in a 3+1 dimensional universe!” to make clear that there are three space dimensions and one time dimension.
But while time and space are different, they’re not completely separate. In very much the same way that the forward direction varies between perspectives, the “future direction” also varies. And in the same way that rotating perspectives exchanges directions, moving at different velocities exchanges the time direction and direction of movement. The total “distance” between points in spacetime is called the “interval”, L. For folk familiar with the Euclidean metric, the “Minkowski metric” should look eerily familiar: 
If you’re wondering, the spacetime interval is a direct consequence of rule #1 in relativity: the speed of light is the same to everyone. The short way to see this is to notice that if you find the interval between the start and end points of a light beam’s journey, the interval is always zero because 
There are two things to notice about the spacetime interval. First, that “c” is the speed of light and it basically provides a unit conversion between meters and seconds (or furlongs and fortnights, or whatever units you prefer for distance and time). So 1 second has an interval of about 300,000 km (one “light-second“), which is most of the distance between here and the Moon. It turns out that the speed at which light travels comes from the “c” in this equation. So the speed of light is dictated by the nature of space and time (as described by the Minkowski metric), not the other way around. Which is good to know.
Second and more important is that negative. That really screws things up. It is arguably responsible for damn-near all of the weird, unintuitive stuff that falls out of special relativity: time dilations, length contractions, twin paradoxes, Einstein’s haircut and marriages, everything. In particular (and this is why the exchange between distance and duration is so unintuitive), if 
This is in stark contrast to regular distance, where if 
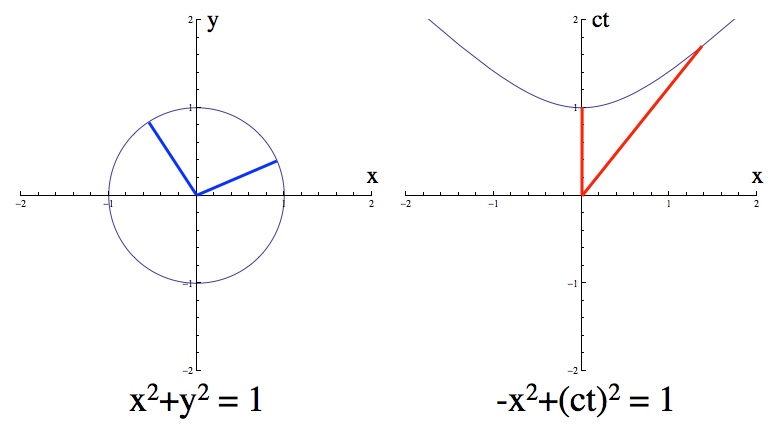
Left: The points a distance of 1 away form the origin form a circle. The two blue lines are the same length. Right: The points a spacetime interval of 1 away from the origin form a hyperbola. The two red lines are the same “length”. Here time is the vertical axis and one of the space directions is the horizontal axis. So if you sit still you’d trace out a path like the first red line and if you were moving to the right you’d trace out a path like the second red line.
Now brace yourself, because here comes the point. The original question was about a journey that, from the perspective of Earth, was d = 4 light-years long, at a speed of v = 0.8c, and taking t = 5 years. The beauty of using “light units” (light-years, light-seconds, etc.) is that the spacetime interval is really easy to work with. The interval between the launch and landing of the spaceship is:
So the interval is L = 3 light-years.
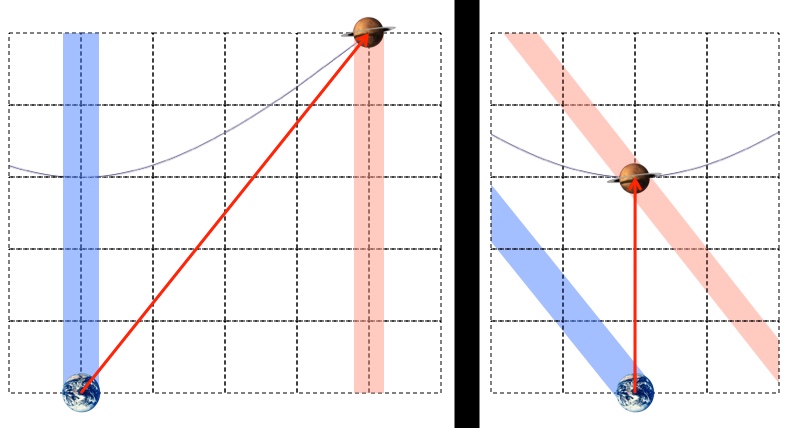
Left: Earth and an alien world sit still (travel through time but not space) 4 light-years apart while a spaceship traveling to the right at v=0.8c takes 5 years to travel between them. Right: A spaceship sits still (travels through time but not space) for 3 years while Earth and an alien world travel to the left at v=0.8c.
Like regular distance, the power of the spacetime interval is that it is the same from all perspectives. From the perspective of the spaceship the launch and landing happen in the same place. It’s like a narcissist on a train: they get on and get off in the same place, while the world moves around them. So d = 0 and it’s just a question of how much time passes:
So, t = 3 years because 3 light-years divided by the speed of light is 3 years.
So just like changing your perspective by tilting your head changes the horizontal and vertical lengths of stuff (while leaving the total length the same), changing your perspective by moving at a different speed changes length-in-the-direction-of-motion and duration (while keeping the spacetime interval the same).
That’s time dilation (5 years for Earth, but 3 years for the spaceship). Length contraction is a little more subtle. Normally when you measure something you get out your meter stick (or yard stick, depending on where you live), put it next to the thing in question and boom: measured. But how do you measure the length of stuff when you’re moving past it? With a stopwatch.
How can you tell that mile markers are a mile apart? Because when you’re driving at 60 mph you see one a minute.
So, like the original question pointed out, if it takes you 3 years to get to your destination, which is approaching you at 0.8c, then it must be 3×0.8 = 2.4 light-years away. Notice that in the diagram with the planets above, on the left they’re 5 light-years apart and on the right they’re 2.4ish light-years apart (measure horizontally in the space direction).
It feels like length contraction should be more complicated than this, but it’s really not. You can get yourself tied in knots thinking about this too hard. After all, when you talk about “the distance to that whatever-it-is” you’re talking about a straight line in spacetime between “here right now” and “over there right now”, but “now” is a little slippery when the “future direction” is relative. Luckily, “time multiplied by speed is distance” works fine.
There are a few ways to look at the situation, but they all boil down to the same big idea: perspectives moving relative to each other see all kinds of things differently. Reality itself, space and time and the stuff in it doesn’t change, but how we view it and interact with it doesn’t quite follow the rules we imagine.
This is a really good explanation. I’ve always struggled with the concepts attendant to relativity, and this article has, in its way, helped me see why. Thank you for your service, AskAMath. I might be dusting off my calc books soon.
Directions in space are not homogeneous…they have different results, depending on how long you travel. Imagine you are on the Globe of the Earth and you travel from the center of the South Pole, North, upward…we would say. When you get to the North pole and you keep traveling, you start moving downward, and you are traveling South. Now imagine you are standing on the Earth’s Equator at say some spot just below Columbia, on the Equator. Now start walking East. Keep walking. When do you start moving West ? Going north on the planet is no problem and it turns into going south. But going East, is always going East…Why ?
Many thanks, great explanation! I wish it was explained to me this way when I was in the uni.
I am wondering: what if some sapient creatures could build a spaceship that moves with the speed of light. (It would not have the rest mass). So all the spaceship and its inhabitants consist solely from particles that move with the speed of light. And all those particles move in exactly the same direction, say direction X. So for these astronauts all objects that they pass will have zero length in direction X and their “normal” lengths in directions Y and Z. So our universe will look two-dimensional to them. But they will pass through the whole universe in zero time, however inside their spaceship the time goes normal, so what will they see in second 1, 2, 3?
@Richard H. Pratt
What you’re describing are issues with coordinates, not with space itself. For example, without very careful measurements of the sky (referencing the Sun or stars) or by asking all the people there, there’s no way to tell that you’re at the south pole. You could be miles away and not know it.
It’s what people in the cartography biz call a “coordinate singularity”.
Klaatu – thank you so much; now I understand a bit better (and only 4 reads!) – you are …. ‘the man’
@Leo
I didn’t want to draw a big line under it, but if a path has a spacetime interval of L, then the time experienced by things traveling along that path is L/c (the spaceship in the post is an example of that). For something traveling at light speed L=0, so no time passes between the start and end of the trip. If you were on a spaceship that (never mind how) traveled at the speed of light, your experience would be: engines on and off, you’re already there.
Makes sense. If there could exist a mechanism of “3D-scanning” people and then “3D-printing” then back, if you scan them on Earth and send to another galaxy and print there, they will feel that the journey took zero time.
Wish my professors explained it like this!
makes sense. conceptually, it is a lot to take in. once you have a handle on it, however, it becomes almost … obvious.
@The Physicist
Good explanation, but I have to do some remarks:
1) When in an answer you say “there’s no way to tell that you’re at the south pole” that´s not true, there are lots of ways to find out, without looking at the stars, e.g. you can look at a sink full of water and observe the whirl when it is draining, depending on clockwise or counterclockwise from the observer point of view, he could know it
2) In the article, you say “Space and time don’t react to how you move around. They don’t contract or slow down just because you move fast relative to someone somewhere. What changes is how you perceive space and time”, but today is my birthday, and I have a twin brother that was invited for me to dinner, he traveled into space like in the Paul Langevin Paradox, he looks much older than me and he insist that today is not his birthday. Is it really just a question of “perspective”?
Thanks
@Daniel Martínez Bertolini
1) With the right equipment you could figure it out (somebody did it). But if you were physically there, with a pot of water for example, you wouldn’t be able to tell the difference between being at the south pole or being a few hundred miles from the south pole.
2) Yup! If you walk straight across a football field (the universal unit of length) you’d say it’s 100 yards long because you walked 100 yards in a straight line. If some kid runs in loops from one side to the other, they might say that the distance is several hundred yards, but that’s because their path is longer. The space itself is the same. In very much the same way, the twin paradox is about taking differently shaped paths, one long and one short, between two events in spacetime.
You start from point A and walk 200 km west, then 200 km north then 200 km east then 200 km south and you arrive back into point A where you meet a bear. What colour is this bear?
@The Physicist
Thanks for you response
Again, …“Space and time don’t react to how you move around. They don’t contract or slow down just because you move fast relative to someone somewhere. What changes is how you perceive space and time”
Suposse I have no news about my twin brother since 2015 and he also doesn’t know he was part of an experiment at Elon Musk’s Spacex where he works since 2010, certain morning during 2015 he went to sleep, he woke up as always, took his car travelling to his job, and he noticed that time had passed, he was in 2019, he didn’t know he was used as space traveller, he called me at home and I invited him to dinner, when we saw each other we were astonished; differences in aging were caused by the different “world-lines” our bodies had followed? In this case, it is not about the volitional act of “perception” that usually could be assigned to a living being, a crystal should have suffered the same effects, actually my twin brother acted more similar to the crystal example. I think I have no questions at all, … just reasoning
I was thinking: how could sapient creatures from all around the universe have contacts and communicate? As the distances are enormous, sending message and receiving response would take hundreds or thousands years which makes the communication impossible. But what if there exist several very advanced races of sapient creatures in the universe, who most of their lives move (perhaps in some kind of spaceships) with very high speed, close to speed of light and only for short periods stop (i.e. stop relative to stars etc)? Say, there are two groups of the creatures, each group moves in its spaceship. (As they are so advanced, they can be very small and in great numbers in a small spaceship and they don’t need whole planet for living). As both spaceships move close to speed of light, their time is nearly similar, i.e. 10 years in one ship is nearly 10 years in the other. But as they constantly move, they can fly and meet each other (stopping for a short period, say, 1 day for conversation) and then continue moving each one its way. So this way multiple civilizations-on-the-move could live and communicate between them. (Whilst civilizations that live statically on planets cannot communicate because of distances).
@Leo – I don’t have any answers on this, and don’t understand the physics well enough, but I wanted to say that I found your idea (beings moving through space close to C and experiencing very little aging) very interesting!
“Good Explanation”
To Richard Pratt
Your North-South, East-West question is about semantics or how we name things.
By defining the two Poles as points on the globe, you can identify movement towards one or the other as heading north or south. If you ignore the existence of the Poles and think about movement along lines of longitude as heading clockwise or anti-clockwise, the direction doesn’t change when you pass either Pole. You continue to head clockwise or anti-clockwise.
Now think of a point on the Equator at zero degrees of latitude and arbitrarily call it the East Pole, with another point at 180 degrees called the West Pole. If you head clockwise from the West Pole towards the East Pole your direction of travel is East. Once you pass the East Pole you are nominally heading West but in reality you are continuing to travel clockwise. Your direction of travel doesn’t change. What changes is how you choose to name your position relative to an arbitrarily defined Pole.
You’re saying that time dilation and length contraction are perspective-type effects. This approach uses an analogy with the (3D seen in 2D) perspective effect we know well. Seems reasonable at first, and the math is similar (though not as similar as it seems at first glance). But the known perspective effect disappears if you change the angle back to the original one, leaving no traces. So why does time dilation leave age differences between objects?
The analogy breaks down, and a truer answer is: ‘we don’t know, but it might be a perspective-type effect’. That’s one of several possible explanations, each with question marks surrounding them.
Also, the perspective idea has major problems if you make time emergent, because in it, the four dimensions all look fundamental. But if you make time not emergent, then you get even worse problems elsewhere. The truth is, this is unresolved, but people often talk as if we know all about it.
@David
When you look at a yard stick from different perspectives, the two ends have different side-to-side lengths. Similarly, the time or distance between two fixed events change depending on your relative velocity.
Totally separate from that, is the length of different paths between fixed locations. Straight along the yard stick is the shortest path between the ends and out to the grocery store and back is a somewhat longer path. Regardless of your perspective, one of these paths is genuinely, objectively longer. Different perspectives may disagree on how far either path extends in any particular direction, but the total length can be measured by anyone (that’s what Pythagoras is for).
The “Twin Paradox” is the “age difference between objects” you’re referring to. It comes down to the different lengths of different paths through spacetime between two fixed events, canonically one twin stays on Earth and the other wanders around space in a rocket. The two paths have objective lengths that can be measured by anyone (that’s what the Spacetime Interval is for), even though different perspectives may disagree on the total time or distance traversed. There’s an old post here that talks all about that. The math will look familiar!
To be sure, there are lots of things in physics that are still open questions. But this particular corner of the field, the nature of time dilation and other basic relativistic effects, are thoroughly understood backwards and forwards.
Knowing the mathematics well is not the same as ‘thoroughly understanding something backwards and forwards’. To say that the nature of time dilation is well understood is out of touch with reality. According to special relativity with the spacetime interpretation, time should not flow at all. There should be no flow of time, this has been rigorously proved. And yet for some reason, special relativity describes the apparent ‘flow of time’, and how it seems to flow at different rates in different situations. That what the equations do – they tell you about the time rate.
Because there should be no flow of time, people used to think the apparent flow was an illusion. But that didn’t work so well, so by around the ’90s, they decided time was an emergent phenomenon instead. But that doesn’t work well either in some situations, for example in the perspective analogy you’ve used, because there, it looks like all four dimensions are fundamental.
The age difference between objects can be explained in the way you have, but that is inconsistent with other explanations. And the perspective analogy goes out of the window, because time dilation leaves lasting effects behind it – which means that it looks like time does indeed flow somehow. Recently, many good physicists have started to think that it does.
Since about 2005, more and more physicists have spoken out against block time, the picture in which time doesn’t flow, including Lee Smolin, and other well-respected people. How can you say that time dilation is well understood? That just isn’t the situation.
The last paragraph has a spelling/grammar mistake! Oh no, I must help!
You said “perspectives moving relative to each other see all kinds of things different”. Here’s what should have been said: “perspectives moving relative to each other see all kinds of things differently”. See the difference? The word “different” should have “ly” at the end.
Hope this helps!
@A Helper Of Grammar And Spelling
Thank you very much!
If I understand it all correctly, if I go from one end of the football field to the other, and my brother went around the outside, and we both get there at the same time, it’s cause my brother traveled faster.
. From your reply to Leo
“For something traveling at light speed L=0, so no time passes between the start and end of the trip. If you were on a spaceship that (never mind how) traveled at the speed of light, your experience would be: engines on and off, you’re already there.”
My question is… when traveling at c, Isn’t the time and distance to Saturn or the edge of the observable universe the same, zero. So the relative distance from you finger to the retro rocket button is also farther away than what ever is in front of the ship? If so, then Wouldn’t the same be true for the onboard computers? If the next moment doesn’t happen until you are slowed, then even programming the ship to slow at a certain time doesn’t happen since the time doesn’t happen until the ship slows.
@Jeff
Absolutely. This is just one more thing to add to the list of why traveling at light speed isn’t a thing.
@Leo I also like the idea of a high speed civilization. If I recall correctly, something like this was done in the later books of Ender’s Game. While Ender had jumped into the future relative to Earth in an early book, his sister joined him later by making a similar jump.