The original question was: If you have a lump of radioactive material with a half life of say 10,000 years, then how come it could start steadily decaying right away? Why wouldn’t everything be relatively stable for 10,000 years and then all of a sudden half of it decays? Like if you buy eggs from the store with an expired date in 2 weeks, you wouldn’t expect one egg to go bad 2 days later, and then another 2 days after that and so on. You’d expect them all to start going bad around the same time.
Physicist: Eggs have an age that they’re “aware” of, in the sense that they change in a predictable way. For example, a fresh egg doesn’t (yet) have a bird in it, while an old egg is either empty of fowl or is foul. By looking at or smelling an egg you can get a sense of how old it is. That’s not true of atoms.
If you know the number of protons, neutrons, and electrons in an atom, then you’re done. There is literally nothing more to know. An atom of carbon-12 (regular carbon) that’s billions of years old is, in every physical sense, totally indistinguishable from a carbon-12 atom created moments ago. In other words: atoms are ageless.
Elements are distinguished by the number of protons, which is the same as the number of electrons, which determines all of the important chemical properties. Different isotopes of an element are distinguished by the number of neutrons. Some isotopes are radioactive and just kinda fall apart, producing alpha, beta, gamma, or neutron radiation (depending on the isotope). Rutherford named the first three in ascending order of penetrating power. A couple pieces of paper will stop most alpha and beta radiation so, since you have skin, gamma rays are the only kind really worth worrying about.
When an atom will decay is unpredictable and doesn’t change with time. A given radioactive atom has some probability of decaying in the next five minutes, say between 12:00-12:05. If it’s still around at 12:05, then it has exactly the same probability between 12:05-12:10. In fact, since no particular time is special, the probability is the same between 12:03-12:08 or any other five minute block.
The more time an atom sits around, the more likely it is to decay. It’s continuously “rolling the dice” to decay or not, and the longer it exists the more opportunities it has. So there will never come a time when the probability of decay is 100%, but given enough time, a radioactive atom is eventually more likely than not to decay. That means we can’t talk about the lifetime of an atom, the time it will take to definitely decay, but we can talk about the “half-life”, the time it will take for the chance of decay to be 50%.
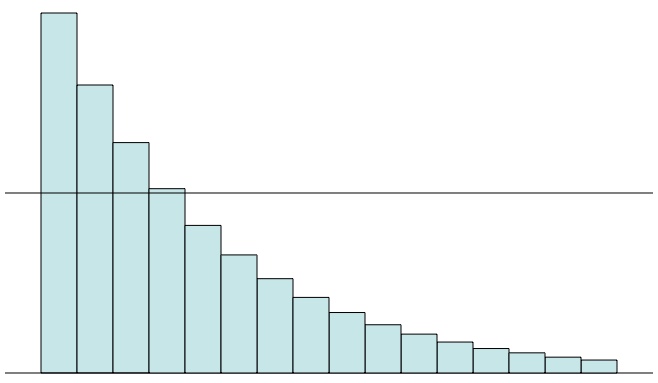
If every minute 20% of the atoms in a sample decay, then at the end of every minute you’ll have 80% of the atoms you had at the beginning of that minute. Here each column is 80% the height of the column to its left. There’s a time where you’ll have lost 30%, or 50% (the half-life), or even 99%, but you’ll never quite lose 100%.
For example, if the probability of decay is 20% in a minute, then at the end of one minute there’s an 80% chance the atom will still be around. After two minutes that chance is 64%, which is 80% of 80%. After three minutes the chance is 0.512 = (0.8)3, or 51.2%. This is because in order for the atom to survive three minutes it has to survive the first and the second and the third, and the chance each time is 80%, because nothing changes (if it doesn’t decay). Following this rule you never get to zero, but you do get to half after a little more than three minutes. This exponential drop is due to the fact that nothing changes for the ageless atoms over time: as far as nuclear decay is concerned, every minute is the same as the one before.
If the half-life of an isotope is h, then the probability, p, that a particular atom will still be around after some amount of time, t, is . What this is saying (in mathspeak) is that after every half-life, the probability that an atom will remain is halved. For example, at t=2h (after two half-lives),
.
There’s nothing special about any particular amount of time. You can plug any amount of time you like into that equation. For example, if h=5 minutes, then after t=7 minutes, the probability that an atom won’t have decayed is .
There’s isn’t even anything special about half-lives. If you get a urge to go rogue on the scientific establishment and start using fifth-lives (and who doesn’t?), you can! If the fifth-life (the time at which an atom has a 1 in 5 chance of not yet decaying) is f, then the probability that it’s un-decayed after time t is .
Normally when you hear about half-lives, it’s in the context of how much of a sample decays in a certain amount of time and not about the lifetimes of individual atoms. Fortunately, “the fraction of a sample that decays” and “the probability of an atom decaying” are one and the same. In practice, you measure probabilities with a large number of trials and fall back on the aptly named law of large numbers to nail down your results. For example, if you wanted to show that the probability of getting tails when you flip a coin is 50%, you’d flip a bunch of coins, divide the number of tails by the total number of flips, and the larger the number of coins the closer the result will be to 0.5 (if you have an afternoon and literally nothing else to do, try it).
As luck would have it, by the time your sample is large enough to see, you’ve got an inconceivable number of atoms. When the amount of radiation exuding from a sample drops by half, there must be half as many radioactive atoms radioacting, and (since there are a large number of them) the probability that any particular atom has decayed must be 50%. But if you’ve only got a few atoms to work with, there’s really no telling (beyond rough estimation) what fraction will be around at any given time.
Typical half-lives are on the order of thousands to billions of years. I say “typically”, because isotopes with really short half-lives are viciously radioactive and decay into other elements quickly, while isotopes with long half-lives can last long enough for some podunk human to find them. For example, uranium 238 (which makes up more than 99% of natural uranium) has a half-life of about 4.5 billion years. That means that it’s barely radioactive and a fair fraction of it will last from whatever stellar cataclysm created it before the formation of our solar system (about 5 billion years ago) to today. And the uranium that remains doesn’t show its age: it’s just as useful, dangerous, and potent as when it was a precocious tyke, drifting around in deep space.







Nice article, simple and clear, thanks
I learned a great amount reading this. The author has a talent for sentence structure and flow. I never need to backread or read the articles multiple times to understand them!
Thank you!
Thanks for explaining half-lives.
I do have one comment though: you said in the picture:
“If every minute 20% of the atoms in a sample decay, then at the end of every minute you’ll have 80% of the atoms you had at the beginning of that minute. Here each column is 80% the height of the column to its left. There’s a time where you’ll have lost 30%, or 50% (the half-life), or even 99%, but you’ll never quite lose 100%.”
But, if you know the mass (or number of atoms) you have, couldn’t you use calculus (i..e limits, series, and convergence) to estimate when you would expect to lose 100%? I guess you could argue that you would need a confidence interval, but could you apply a limit to that confidence to get it to 100%?
(I actually think I know why this won’t work, but if you’ll let me I’d like to play devil’s advocate here, especially since I’m not the best at articulating the thoughts).
(I’m thinking of the Dichotomy paradox, by the way, from here: https://en.wikipedia.org/wiki/Zeno%27s_paradoxes)
@Locutus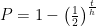 . If there are N atoms, the probability that they will all have decayed is
. If there are N atoms, the probability that they will all have decayed is ![P=\left[1-\left(\frac{1}{2}\right)^{\frac{t}{h}}\right]^N P=\left[1-\left(\frac{1}{2}\right)^{\frac{t}{h}}\right]^N](//s0.wp.com/latex.php?latex=P%3D%5Cleft%5B1-%5Cleft%28%5Cfrac%7B1%7D%7B2%7D%5Cright%29%5E%7B%5Cfrac%7Bt%7D%7Bh%7D%7D%5Cright%5D%5EN&bg=ffffff&fg=000&s=0) . That power of N (which is typically north of 10^36 or so for objects big enough to hold in your hand) forces numbers that are even slightly lower than 1 down to nearly zero.
. That power of N (which is typically north of 10^36 or so for objects big enough to hold in your hand) forces numbers that are even slightly lower than 1 down to nearly zero.
This is something you can play around with yourself. You’re right, about the best you can do is a very wide confidence interval.
If the half-life is h, then the probability that an atom will have decayed after time t is
‘It’s continuously “rolling the dice” to decay or not’. This analogy really works for me.
I imagine coming to a roulette table and sitting next to a person who’s been on a winning streak by just betting on black, not willing to leave until the roulette table hands them a losing red number. I do not know how long he has been sitting there, betting on black. He may have sat there just minutes before I arrived, or he may have been betting on black since yesterday. However, it doesn’t matter how long he’s sat there; those past bets don’t affect his future chances of losing his next bet.
@Roy S.
Exactly!
I feel like the fact that atoms do not appear to have an ‘awareness’ of time in a linear, ongoing manner like this probably says something rather important about the true nature of time versus the way we perceive it.
But I’ll be damned if I can figure out what that something is.