Physicist: The last five chapters should have left you terrified. These should leave you inspired. With all of the mathematical tools established, these lectures get into some of the remarkable things that quantum hardware can do.
Quantum cryptography in a nutshell.
Lecture 12: Quantum Communication
Lecture 13: The Quantum Fourier Transform
I have a lot of catching up to do and I intend to read all 15 of these 🙂 but I noticed that you showed that Grover’s Search is O(Sqrt(N)) and you proved it can’t be any faster.
The Wikipedia page says the same thing but it also talks about a non-local hidden variable computer that can do it in O(Cuberoot(N)). Is this due to some limitation to what we call quantum computers (versus whatever a non-local hidden variable computer is)? (Or do I need to read all first and that answers the question for me?)
@Locutus![\sqrt[3]{N}](//s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7BN%7D&bg=ffffff&fg=000&s=0 "\sqrt[3]{N}")
result before. I skimmed the paper (you’ll be glad to know that these five lectures should make it fairly readable). I’m not sure if the Aaronson seriously believes that this is physically realistic or if he’s just excited about an (admittedly very interesting) strictly mathematical result.![\sqrt[3]{N}](//s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7BN%7D&bg=ffffff&fg=000&s=0 "\sqrt[3]{N}")
ever being used in any physically real context.
I’m glad someone is enjoying these (other than my students, who must enjoy them).
I’d never heard of that
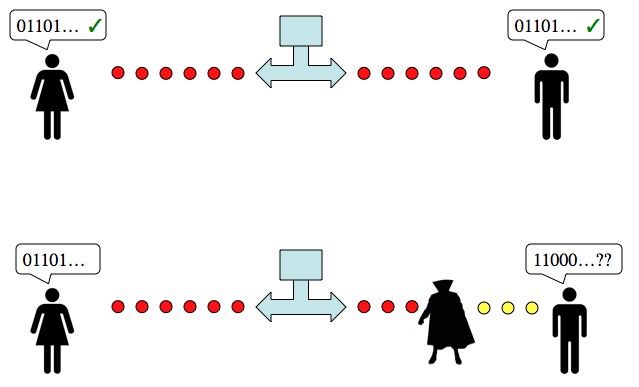
“Non-local hidden variables” should raise red flags. Hidden variables are things that, by definition, can’t be taken into account and non-local means you’re relying on effects “just kinda happening” between things that aren’t interacting in any way (for example, from across the universe).
If I had to put money on it, I wouldn’t bet on this particular
No April fools this year?