Mathematician: That depends on what you mean by “universe.” Here’s a framing:
A circle of radius R centered at a point P is the set of all points in the plane with distance R from P. The diameter D of this circle is twice the radius, but can also be thought of as the longest possible straight-line path from a point on the circle to another point on the circle. The circumference C of the circle is its arc length. By definition, Pi = C/D.
We usually think about distance as “how the crow flies” and the shortest path between two points is a straight line, but think about how you might get around in a well-gridded city. You either walk north to south or east to west. You can turn at corners, but each moment spent walking is either purely vertical or horizontal. If a mathematician gridded a city, we might think about (0,0) as the city center (the intersection of 0th Ave and 0th St). What points are exactly 5 blocks away? Clearly (0,5), (5,0), (0,-5), and (-5,0) (yes, negative streets and avenues!) have shortest distance paths of length 5. But so do (2,3) and (-1,4). You can convince yourself that to get to the point (a,b), you’re going to have to travel at least |a| in horizontally and |b| vertically, so the distance from (0,0) to (a,b) is at least |a|+|b| blocks, and it’s easy to see a path that gets you there in exactly |a|+|b|. There might be many paths from (0,0) to (2,3) (consider ENENN or NENEN or NNNEE, for a few northeastern routes there), but all of the shortest ones take 5 blocks, like these.
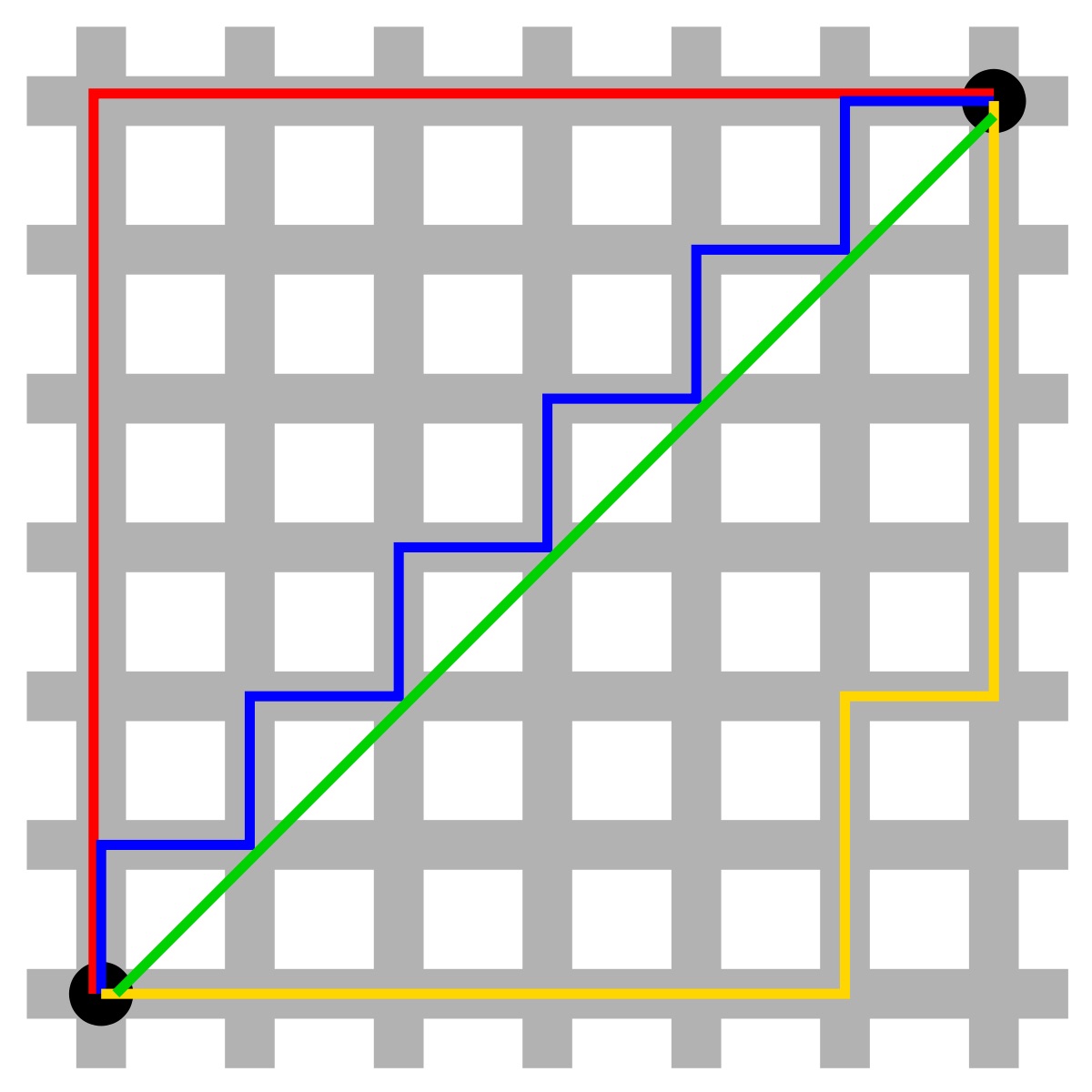
Two points separated by a taxi cab distance of 12. The red, blue, and yellow routes all cover 12 blocks. The green line is the “how the crow flies” distance.
If we accept this “taxi cab” sense of distance, we can consider all of the points that have distance R from (0,0) and we would find it looks more like a diamond, since they satisfy |x|+|y| = R instead of sqrt(x^2 + y^2) = R. The boundary is actually given by four lines:
x+y = R
x-y = R
-x+y = R
-x-y = R
which gives the outline of a square at a 45-degree tilt. Each of the side segments has length (in the usual sense of length!) of R*sqrt(2), but we might want to stick to our taxi cab sense of distance and instead of concluding the perimeter has length 8*R instead of 4*R*sqrt(2), the logic being the distance from (0,R) to (R,0) is 2R and we have to make 4 such trips to wind around the perimeter. If we take two points on the perimeter (a,b) and (c,d), the distance between them will be |a-c| + |b-d|, which you can convince yourself will always be less than or equal to 2R (regardless whether your sense of length is the usual or the taxi length!) and equals 2R from one far corner to another, so we might feel comfortable calling the “diameter” of this “circle” 2R. In this case, our taxi cab Pi would be Pi = C/D = (8R)/(2R) = 4.
Different notions of distance produce different notions of Pi. If you know some calculus, you might get a kick out of this paper, which explores Pi as this ratio with respect to a bunch of different related distance systems, including both our usual system, this taxi system, and a spectrum that both lie on:
https://www.jstor.org/stable/
If you’re committed to the usual notion of distance, then we’re stuck with the 3.14159265… business.
Physicist: There are a lot of physical constants in the universe; the strength of gravity, the strength of electric fields, the speed of light, the rate of the universe’s expansion, and on and on. The vast, vast, vast majority of the possible combinations of values of these physical constants produce boring universes, like a single huge black hole or just diffuse clouds of hydrogen without stars. There doesn’t seem to be a good reason for the constants to be what there are, save one: there are critters (people) running around saying things like “What’s going on? The universe is so inexplicably balanced that I can exist and say things like ‘What’s going on?’.”
The philosophy here is a little pessimistic. Existence isn’t kind, it just accidentally has pockets where it’s not actively mean. For example, given the absolutely over-the-top number of planets in the universe, it’s not too surprising that at least one of them isn’t completely inhospitable and not surprising at all that we happen to live there. The argument for there being lots of universes with different physical constants is similar. Nobody likes either scenario a lot. If there’s one universe that happens to be nigh-perfect then we need a lot of luck, and if we don’t want to invoke luck, then we need lots of universes. All that to say, it’s not completely unreasonable to suppose that there are lots of universes and that π might take different values.
However, there’s a big difference between physical constants and mathematical constants. For example, the gravitational constant (a physical constant) is 
The strict “circumference over diameter” definition of π can have different values depending on the nature of the space involved. For example, in a curved space (or when restricted to a curved surface) we can measure the circumference and diameter of a circle and find that π is smaller than it should be, because the diameter has a longer trip and is longer than it “should” be.
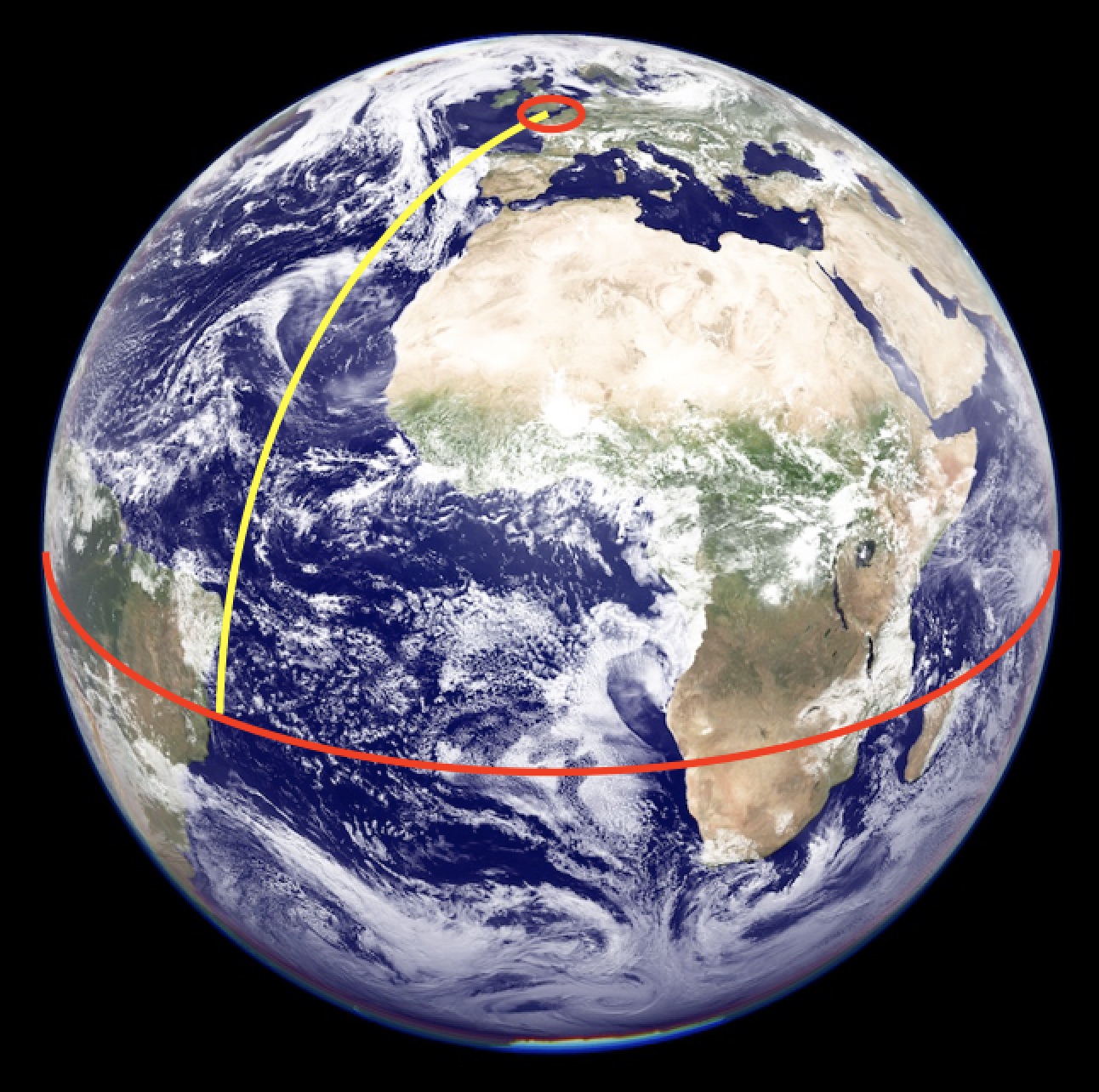
π is the ratio of the circumference (red) to diameter, which is twice the radius (yellow). If you’re stuck on a sphere using a small circle you find that π=3.1415… and if you use the largest possible circle you find that π=2.
All the same, the denizens of a curved spacetime don’t need to be too dumb to figure this out. After all, space near Earth is slightly curved (that’s why we have gravity) and that hasn’t interfered with us imagining it flat (dumbness notwithstanding). If they can imagine Platonic ideals, then with a little work they can figure out how to calculate π just like we have. All that those other-worldly denizens would need is some notion of smooth space, since small circles in smooth space produce the usual value of π (this is basically the definition of smooth space).
So, do other universes have space like we do? Unfortunately, we’ve got no experience with other universes and no solid evidence that they exist at all. What we have are scientific speculations (which is what you get when a scientist guesses). There’s no standard definition for “parallel universe”, but here are two lists of ideas. In a nutshell there’s: 1) same universe, but far away, 2) quantum multiverses, 3) related universes with different constants, and 4) “other”.
When things are far enough away, there’s no way to affect anything over there and vice versa, so those places may as well be other universes. But they’re not really. Same π.
In the Many World’s interpretation of quantum mechanics the universe we live in seems to split into separate universes. You’re in a not-special one of them and evidently they’ve got normal space. Same π.
String theory and eternal inflation imply that new universes are constantly being formed with slightly different physical constants. Lee Smolin’s “Fecund Universe” theory, where every new universe is a black hole from a higher universe, implies that universes literally evolve to be better at producing black holes. I like the second idea better than the first, not because either is terribly convincing, but because it’s a cooler. It scratches a brain itch. That said, in both of these ideas the new universes are “built on the same scaffold” of spacetime with different numbers of dimensions perhaps, but with the usual notion of space and distance and therefore: same π.
Finally, physicists will sometimes include a catch-all to acknowledge that not everything is known and because as much as we learn, there are always (or at least often) surprises. That’s the “other” and it’s not really worth worrying about, because… what are we supposed to worry about? There may be universes out there with completely different notions of distance, but we wouldn’t even recognize them. In that “maybe… somewhere… somehow…” sense, π can definitely be different.
Science is a god unto self, with distanes so far, who knows, but science cannot accept insight from other means such as alien intelligence, or souls from other universes!
There are very few problems in physics that don’t appear to be solved if you postulate trillions of unobservable universes, with varying laws. If you’re prepared to make that many assumptions, and take on all that baggage, you can explain just about anything.
But physics narrows things down to get to solutions, and explains things using as few assumptions as possible. Many universes does the opposite. It opens things up so wide, that you can seem to explain anything. But there’s just one problem – you’ve left physics behind. Many universes is what people go to when they’re stuck. They like to say, oh, well, we know the answer. But the great physicists admitted when they were stuck, and took on the challenge, and that’s how they got to real solutions. If you don’t admit you’re stuck, you’ll never make progress.
What a nonsense post!
“That depends on what you mean by “universe.” “[undefined]
“If we accept this “taxi cab” sense of distance”[no we don’t]
“In that “maybe… somewhere… somehow…” sense, π can definitely be different.”[hand-waving horseshit]
“I like the second idea better than the first, not because either is terribly convincing, but because it’s a cooler. “[ ignore whether its true, false or even meaningless ]
depends on what you mean by “Pi”
etc etc etc
what total excrement !
To be fair to the ‘ask a’ guy, the question was speculative already, and of the kind that is bound to lead to partly speculative answers. If you don’t like speculation, I think the one thing we can say is that in a different space, it might be possible for pi to be different, but in a background space identical to the one we live in, it’s going to be the same.
Signs that the dismal 2020 is in the rear view. Vaccine has arrived and, the Mathematician has returned. Things are looking up.
@Josh,
TL;DR: Pi is only a constant if the definitions of distance and the universe and so forth are constant. Trouble is, there’s nothing to keep you from using different definitions, and in many cases, there are good reasons to use a different defintions.
Forgive me, but I have a hard time understanding where you are coming from in your comment. I find this post to be a very reasonable answer. It answers the question: the answer is both yes and no. And how much more specific could the answer get when discussing other universes, which we have no experience of?
To your points:
1. On an undefined Universe.
The Physicist defines several types of extensions to our own universe. “In a nutshell there’s: 1) same universe, but far away, 2) quantum multiverses, 3) related universes with different constants, and 4) “other”.”
(1) basically takes the concept of our observable universe and says “same universe, but beyond what we can observe”. That’s fairly well defined. (2) is also well defined: same universe, just different possibilities (i.e. I ate chicken nuggets for breakfast this morning instead of yogurt or nothing at all). (3) is also well defined: take the physical constants and tweak them. But logic and math remain the same, and so does pi. (4) is the catch-all, and that’s not so easily defined, because if it were well defined, it would be a contradiction to say it is “other”. Here, there be dragons, and the value of pi could hypothetically be different. And how could it be different? Well…
“If we accept this “taxi cab” sense of distance”. And, contrary to your comment that we do not, it turns out that we actually do (I personally do on many occasions, I’ll explain in a bit)! Taxi cab distance is more commonly known as Manhattan distance, and if you ever pay for a taxi in Manhattan you are not only accepting this sense of distance, but your wallet is paying for it, as well.
I’m a data scientist, and we use different senses of distance, including Manhattan distance, all the time. The usual notion of distance that most people think about in geometry is Euclidean distance, and while it may have many, many uses, it is hardly a perfect metric. There are many cases where it can not be used to adequately describe distance at all. Take, for example, binary information in high dimensional space. It is often far better to use Jaccard distance than Euclidean.
And yet, even when we are using different notions of distance, we can still describe concepts like the “center”, “perimeter”, and even “area”. It makes perfect sense that we could thus describe a circle in this type of space, and since the distance metric is different, so too is the value of pi.
Now, if you use Manhattan distance, what size of city block should you use? If you get smaller and smaller, you can get more precise. And this is what The Mathematician alludes to when the use of Calculus is brought up: take the limit as the size of these blocks goes to zero, and you end up with something that looks a lot like Euclidean distance. (In fact it might even be Euclidean distance, but I’m not going to go through the mathematical exercise to prove or disprove it. But what you end up with is a line that follows “how the crow would fly” from one point in the city to the other.)
Now, this is all well and good in the data science or conceptual arena, but you might be tempted to say that this does nothing to show if a universe physically operates according to these “unusual” distance metrics or not. The counter is this: there is nothing to say that *our* universe operates according to Euclidean distance, either.
Distance metrics are just models. We humans invented them. We even have a criteria to define what qualifies as a “metric” and what does not (things that do not qualify can’t be used to measure “distance”). We choose one or the other because they are useful and tend to work well. In physics, Euclidean distance is almost always the go-to. But it’s just a model, a way we humans have figured out to describe the universe in a way that just works for the problems we like to solve.
And the mathematical objects like circles, cones, and spheres are also models in the same way. The different aspects of these shapes like the perimeter, vertices, and so forth are there because they are defined to be there. What follows then are the relationships between the different aspects of the shape (like pi), and they come to exist based on those definitions and the mathematical principles we’ve agreed to operate on. Traditionally that’s Euclidean distance, but there’s nothing (except ourselves) that says it absolutely *has* to be Euclidean distance.
So, after all that, the answer to the question “Can pi be different in another universe” really is the same answer to the question “Can pi be different in our own universe”. And the answer is certainly *yes*, it can be different, if we change the definition of distance or if we curve space. If we don’t do either of those things, then the answer is “in our own universe, no, pi can’t change, not really, but we humans are ignorant about many things, so, maybe, somehow, in another universe, it could be different”. Let me be clear: this is not a horseshit answer, this is an admission that we humans are not gods and do not know or have experienced everything. It’s as honest of an answer as you are going to get: we don’t really know what another universe is like (actually we don’t even know if they exist), and so while we can guess as to what extensions to our own universe might be like, we can’t say anything at all about things outside of what we understand.
As for the Physicist’s statement that he likes the second idea better than the first, well, it is just a preference. And there’s no scientific reason (yet) to prefer one over the other (@Physicst, please correct me if I am wrong). So we can throw out logical thinking, true and false, for the moment. Why? Because we don’t know. We can’t say which is true or false, all we can do is guess. So prefer one or the other because you fancy it if you like, because one of them stirs up your imagination more than the other (that seems to be the Physicist’s reason, at any rate).
So Josh, the very nature of the question that the Mathematician and Physicist are trying to answer requires that the answer be non-specific. In our universe, in fact in various occupations (data scientist, mathematician, physicist, accountant, etc.) there are different ways of measuring the “center” of things and points which are supposedly equidistant from that center (meaning a circle, sphere, or hypersphere). Each method is perfectly valid, and the resulting relationship between radius and circumference changes accordingly, as does pi.
Horray! The mathematician’s back!
I subscribe to your weekly helpful ideas, Mr Mathematician. Glad to have you back on ask a mathematician!
Reading between the lines in a number of posts, the subtle undertones suggest to me that people prefer calling him The mathematician. I think that’s right, sorry I called him the ‘ask a’ guy. It wasn’t meant to be derogatory, and I respect some of his articles a lot. Someone once called him that a while ago, and I thought that people called him that.
@David
Some of us curious fans know their real names, but I find it more polite to just address them as “mathematician” and “physicist”
where’d that portuguese guy go? His thing disappeared!
Oh wow, it’s been a while since we’ve seen the Mathematician – welcome back dude!
@David: Actually, multiple universes is what we get if we make the smallest number of assumptions.
If we simply don’t assume (because it’s never been proved) that there’s a size at which Physics transitions from Quantum to Classic Mechanics, then it means everything at all scales is in Quantum superposition. Hence, multiple universes.
If, on the other hand, we assume there is this transition, for example, that there is physically a phenomenon such as the collapse of the wave function, and that we only need to look harder until we can finally find at which scale exactly it happens, then macroscopic things cannot be in any Quantum superposition. Hence, a single universe.
If we go for Occam’s Razor, which prefers less assumptions to more assumptions, then the first option is the best. It requires one assumption less, at the cost of multiplying the outcomes.
If we go *against* Occam’s Razor, preferring to *add* one assumption so as to *contain* the outcomes, then we get one universe, but for many the price of an unproven, unfindable, extra assumption is too high.
So, pick your poison, because there doesn’t seem to be any situation in which both a minimal number of assumptions and an outcome of a single universe coexist.
[Desafio a Nasa], sobre este enigmático número de “Pi”, uma grande descoberta inovadora, A Matemática andando na contra mão; com nome, sobrenome e denominação de origem, o passado jamais esteve tão presente por dentro da Ciências Exata, sendo a pioneira entre os pensadores e os(as) Matemáticos(as) em tempos passados, pois foi em cima de ombros de gigantes que enxerguei o horizonte na visão da Matemática, com esta grande única e majestosa descoberta sobre este enigmático número de “Pi”,uma descoberta inovadora, com duas casas depois da vírgula uma medida com total precisão para os cálculos de “Pi”, onde poderá mudar a história da Matemática, trazendo uma realidade acima de qualquer suspeita, provando Matematicamente que com sua precisão será uma descoberta inovadora no quesito Matemática, onde irá facilitar a explorar o espaço e o Universo, enviando sondas para todos os planetas jamais descoberto, e trazendo grandes informações de como um planeta é habitado, simples, preciso de uma simples razão para ter uma precisão jamais vista em todos os tempos, com muita investigações, muitos estudos e pesquisas cheguei ao um único número de “Pi”, sendo totalmente Racional com várias razões de números inteiros e 270 fórmulas para seus cálculos, pois cada fórmula desenvolvida, tem que saber sua essência para ser tão bela com resultados surpreendentes.O Autor Sr Sidney Silva.
@Alexander Gieg: this is completely wrong. If you don’t want excess assumptions, like the minimum that is needed in physics and philosophy generally, then we’d better look at some of your statements, which contain false assumptions. You say:
“If we simply don’t assume (because it’s never been proved) that there’s a size at which Physics transitions from Quantum to Classic Mechanics, then it means everything at all scales is in Quantum superposition. Hence, multiple universes.”
You’re wrongly assuming that we’re in a position to talk about how QM should be interpreted. We’re simply not. Above all, we don’t know enough about superposition for what you’ve said. You’ve said things from your own view of QM, which others would completely disagree with.
“….then it means everything at all scales is in Quantum superposition. Hence, multiple universes.”
No it doesn’t, this is false. We don’t know if it means that, it depends on the nature of superposition.
“Hence, multiple universes.” This bit is particularly false, if you don’t mind me saying so. We don’t know anything like enough about what’s underneath QM to say things like that.
As I sometimes say to the physicist, you have to admit what you don’t know, and leave holes in the jigsaw accordingly. The failure to do this is the commonest mistake in physics.
Many of us think that in QM there’s something emergent going on at larger scales. The transition between quantum and classical behaviour looks like it’s about the transition to emergent behaviour. We know without any doubt, from decoherence, that interaction with a particle’s environment leads to a superposition rapidly decohering, and so dissappearing. Interactions do this – it comes both from theory, and more recently from experiment, since the late ’90s. And we know this century that the larger the object in question, the faster it decoheres. This is our first step in grasping the scale issue in QM, but you don’t even seem to know about it. Read up on decoherence. You’ll find out that the entire universe is not in a superposition.
As always, the fewest assumptions goes with a single universe. But you need to face the fact that, like in every other era of physics, there are things about the universe we don’t yet understand. If you face up to that, you’ll find that many universes is a huge number of assumptions, made in an attempt to run away from tackling the problems that are in front of us.
@David: “You’re wrongly assuming that we’re in a position to talk about how QM should be interpreted. We’re simply not.”
Well, most physicists disagree with, since there are several interpretations of QM, every physicist having their preferred one. These interpretations are all compatible with the equations, so choosing one over the other is a matter of preference and a few philosophical assumptions here and there. Here’s a list and even a table organizing them:
https://en.wikipedia.org/wiki/Interpretations_of_quantum_mechanics
But sure, we can also have QM with no interpretation whatsoever. That’s taking the equations alone, without doing any attempt at making them intuitive in any way whatsoever. It also works, it’s just hard to do.
“You’ll find out that the entire universe is not in a superposition.”
So, that’s precisely what is in dispute. That us not observing the universe being in a superposition is no different from the photon traveling in one slit of the double-slit experiment not observing itself in a superposition with the photon traveling in the other slit of the experiment. As a part of a universe in superposition you wouldn’t know it either. Ditto for the speed of decoherence, which may also merely be the speed of splitting.
The theory admit both. So, if it makes no difference, why bother with the QM interpretation one prefers? As long as everyone is doing science in a rigorous way, that’s what matters.
In the 20th century, we didn’t really find anything out that limited how QM can be interpreted – only Bell’s theorem. But the view you’ve given that we have no limits on how it can be interpreted is way out of date, perhaps 30 years.
As you’ve talked about the scale issue in QM, and used it as part of a point you made, I’ll do the same. What we know about the scale issue this century is this: you get superpositions at the quantum scale, but not at any larger scale, if the matter interacts with other matter. There is no such thing as a large scale superposition – not for long. In a tiny fraction of a second the matter interacts with matter in its nearby environment, and the superposition immediately disappears. The larger the object that this happens with, the faster it happens. It takes a non-zero, very short period of time that we can calculate – Zurek published an equation for getting the time period way back in 1984. So the scale issue is getting clearer – we know more about it. Large objects lose their superposition faster than small ones, and we have the math for that.
Since then it has been confirmed by experiment, and the mathematics of decoherence came out of the original quantum theory – no-one is questioning it. Because interactions cause this to happen for some reason, coming out of both theory and experiment, it becomes clear that when we make a measurement, the interaction needed to make the measurement is probably the cause of ‘wave function collapse’.
This is still counter-intuitive, which is why many haven’t heard much about it. But although we still don’t have an interpretation, not with any consensus, we have more than just the equations – we have limits on how QM can be interpreted. (The Frauchiger-Renninger paper of 2018 added to this.) So nowadays you can’t just imagine the entire universe to be in a superposition, we know that large scale superpositions don’t exist longer than a fraction of a second.
Well, we’re off-topic here, sorry about that!
@David “There is no such thing as a large scale superposition”
I’m sorry, what? Superposition has been demonstrated in molecules comprised of up to 2000 individual atoms, is that not large enough for you?
There is absolutely no reason to assume that superposition has some kind of arbitrary scale restriction, it is simply more difficult to demonstrate superposition as things get larger, as larger things have larger waveforms and the size of the waveform rapidly becomes prohibitively gargantuan. (IIRC there’s an article on this very site that estimated the necessary length of a double-slit experiment to demonstrate superposition on bosonically identical cats to be approximately the distance between Earth and Jupiter, for example.)
@Neruz. The sentence you quoted had three more words: ‘not for long’. The system collapses with or without a measurement soon enough – that is if it is not shielded from its environment. It’s possible to keep a superpositon intact for longer if we do some contrived things to it. But we’ve found a mathematical relationship between scale and the time it takes for the superposition to go. And when it decoheres, we know for certain that entanglements are being created with the surrounding matter. We don’t know what entanglements are, but a lot of them get created very quickly.
If we’re trying to get clues about what’s going on underneath QM conceptually – and I’d say real progress can only be made if conceptual progress is made – decoherence has brought some vital new clues. As always, how we interpret what we know is partly a matter of taste, but I’d say the idea that the whole universe can be in a superposition is out of date. Before the ’90s, people who had all the clues at their fingertips used to think that sometimes, but not since then. It’s hard to take onboard clues that we don’t understand, but it’s the only way forward, and I believe they’ll make sense to us one day.
Hi guys,
How to interpret these REAL experimental results, which are described in the
link https://www.youtube.com/watch?v=xX14NK8GrDY&ab_channel=PeterAxe ?
Looking forward to your answer.
Most modern mathematicians would say that pi is a specific numerical constant given by various expressions such as 4(1/1-1/3+1/5-1/7+…), and that even in a universe governed by a different geometry, pi would still be 3.14159… To get a universe in which pi “had a different value”, you’d need to change the way numbers behave (whatever that might mean), not just the shape of space.
Some of you might reply “I thought the definition of pi was the ratio of the circumference of a circle to its diameter!” And indeed this once was the definition of pi. But (in the immortal words of Inspector Clousseau), Not Any More.
[Desafía a la NASA], debido a que la NASA a menudo usa el valor de pi igual a (3.141592653589793) quince dígitos después de la coma sobre este enigmático número de “Pi”, reportaré un gran descubrimiento; Matemáticas a contrapelo, con nombre, apellido y denominación de origen; El pasado nunca ha estado tan presente dentro de las Ciencias Exactas, siendo el pionero entre pensadores y Matemáticos en tiempos pasados, porque fue sobre los hombros de gigantes que vi el horizonte en la mirada de las Matemáticas, con este único gran y majestuoso descubrimiento sobre este enigmático número de “Pi”, un descubrimiento innovador, con dos dígitos finitos después de la coma (3,15) una medida con total precisión para los cálculos de “Pi”, que podría cambiar la historia de las Matemáticas, trayendo una realidad más allá de cualquier sospecha, demostrando Matemática y Científicamente: que con su precisión será un descubrimiento innovador en la categoría de Matemáticas, que facilitará la exploración del espacio y el Universo, enviando sondas a todos los planetas jamás descubiertos, y trayendo gran información de cómo un planeta está habitada, simple, necesito una razón simple para tener una precisión nunca vista en todos los tiempos, con muchas investigaciones, muchos estudios e investigaciones llegué a un solo el número de “Pi”, siendo totalmente Racional e Irreversible, con uno y varios ratios enteros y 270 fórmulas para sus cálculos, porque cada fórmula desarrollada, tiene que conocer su esencia para ser tan bella con resultados sorprendentes. El Autor Sr. Sidney Silva; de la obra “La audacia de que pi sea racional”
Increíble: reportaré nuevos descubrimientos dentro del enigmático número de π; las raíces cuadradas exactas y no exactas es igual al número enigmático de π (√2; √3; √4; √5; √6; √7; √8; √9; √10; √11; √ 12; √13; √14; √15; √16; √17; √18; √19; √20; √21; √22; √23; √24; √25; ……… ….. .√877; …………… √350734139; y el enigmático número áureo también es igual al enigmático número π, lo que demuestra científica y matemáticamente mi “Tesis”, el autor Sr. Sidney Silva.
if a laser beam travels back and forth between mirrors, you would almost definitely need more decimal places than NASA suggests….
What this teaches us is that if you change dimensions, you have different rules. In a two dimension world you cannot have a sphere – and pi exists only in one dimension. So – in the taxi diagram showing how you get from point A to Point B you can only take the green line if you are in three dimensions. Which explains why accessing the fourth spatial dimension is so important. Of course, we have to agree on what that is. . .
Is there someone I can talk to about a theory i have or the math equations i am trying to create to explain or measure my ideas to. I need to know if im just spinning my wheels?!
Dear Sir(s) of this simple page, I have read some comments, but I was not very satisfied to see that everyone persists in affirming that this enigmatic number of pi is irrational, in my concept in the current era it is a Rational number, as I’ve been reporting for some time now; everyone does not realize that any proof will be approximate, the proof is based on a conjecture that has not been proved. Is this good practice? If the conjecture is wrong, then the work would be null and would fall to the ground, completely losing its strength of past times. Sir Sidney Silva.
Dear noble friends, professors, students, acquaintances of this simple channel, with my respect to everyone present here; what impact would it have on the Universe of Mathematics, by stating that some numbers cited are not prime? and the Twin Cousins do not exist?
two; 19; 41; 59; 61; 79; 101; 139; 179; 181; 199; 239; 241; 281; 359; 401; 419; 421; 439; 461; 479; 499; 521; 541; 599; 601; 619; 641; 659; 661; 701; 719; 739; 761; 821; 839; 859; 881; 919; 941; 1019; 1021; 1039; 1061; 1181; 1201; 1259; 1279; 1301; 1319; 1321; 1361; 1381; 1399; 1439; 1459; 1481; 1499; 1559; 1579; 1601; 1619; 1621; 1699; 1721; 1741; 1759; 1801; 1861; 1879; 1901; 1979;
However, the “Rielmann Hypothesis” completely loses its strength in the theories of past times, however this prize that the Clay Institute wants to pay, will not be able to pay for an unfounded theory, since these numbers are not prime, it can totally change the history of Mathematics, bringing Innovative Mathematics to the current era, my concept of what a prime number is, I sanctioned a Law that must always be respected; for every prime number, where it will be factored from the smallest to the largest, and from the largest to the smallest only with the prime numbers themselves, so it will be considered a prime number …. follows how my thesis will be:
I will multiply only with prime numbers, respecting my law:
3*5*7*11*13*17 = 255255
255255 3
85085 5
17017 7
2431 11
221 13
17 17
1
In this first example it was from smallest to largest;
255255 17
15015 13
1155 11
105 7
15 5
3 3
1
In this second example it was from the largest to the smallest, only this pattern can say that it is a prime number. Sir Sidney Silva.
The number image for pi on the earth (small circle pi = 3.14etc; largest circle pi =2) can be extended to the cosmos (our universe).
In reality (so to speak), we will have to measure large distances not with material rulers, but with light, or actually, time. Straight-line measurements would be easy: aim a laser to a mirror and time the path for a return. Measuring an actual light beam around a circle will be tougher, but can be imagined. In fact, imagining the whole thing will be simpler.
Let’s do this: imagine a large region of space – several Astronomical Units, or even a Light Year. In the center of this space is a star, or better, a black hole – a massive black hole. Measuring the diameter by a straight line right thru the center is not possible, but by taking a few measurements and correcting for angles slightly off-center, we can get an accurate experimental measurement which takes into account the gravitational effect of time slowing, so our experiment gives a larger distance than would be calculated from the non-gravity-influenced circle of space (imagined) at the circumference. This gravity-influenced pi would be less than 3.14etc because the diameter would be longer, due to slower light speed.
Now space is full of mass – it’s lumpy. It’s not flat in a 3-dimensional sense. So, I propose that pi is a mathematical concept equal to 3.14etc, but in reality, the ratio of the circumference to the diameter of a particular circular region is equal to 3.14etc only for “small” regions (~millions of miles), and can be significantly less than that near massive objects.
I wonder what that means for other “universal” physical constants that depend on pi.
Maybe physics is not the same everywhere in the universe. Or chemistry!