The original question: I’m having a debate with my wife that I think you can help us resolve. We have a swimming pool in our back yard. It has an electric heater, which we set to keep the pool water at 85 degrees Fahrenheit. We’re going to be away for three days. My wife says we should turn the heater off while we’re away to save energy. I say that it takes less energy to maintain the pool at 85 while we’re away then to let it drop about ten degrees (summer evenings can get quite cool where we live in upstate New York) and then use the heater to restore 85. Who’s right? And what variables are relevant to the calculation? The average temperature for the three days? The volume of the pool? The efficiency of the heater?
Physicist: The correct answer is always to leave the heater off for as long as possible, as often as possible. The one and only gain from leaving a pool heater on is that it will be warm when you get in. The same is true of all heaters (pool, car, space, whatever).
You can gain a lot of intuition for how heat flows from place to place by imagining it as a bunch of “heat beads”, randomly skittering through matter. Each bead rolls independently from place to place, continuously changing direction, and the more beads there are in a given place, the hotter it is.

If all of these marbles started to randomly roll around, more would roll out of the circle than roll in. Heat flow works the same way: hotter to cooler.
Although heat definitely does not take the form of discrete chunks of energy meandering about, this metaphor is remarkably good. You can actually derive useful math from it, which is a damn sight better than most science metaphors (E.g., “space is like a rubber sheet” is not useful for actual astrophysicists). In very much the same way that a concentrated collection of beads will spread themselves uniformly, hot things will lose heat energy to the surrounding cooler environment. If the temperature of the pool and the air above it are equal, then the amount of heat that flows out of the pool is equal to the amount that flows in. But if the pool is hotter, then more “beads” will randomly roll out than randomly roll in.
A difference in temperature leads to a net flow of heat energy. In fact, the relationship is as simple as it can (reasonably) get: the rate of heat transfer is proportional to the difference in temperature. So, if the surrounding air is 60°, then an 80° pool will shed heat energy twice as fast as a 70° pool. This is why coffee/tea/soup will be hot for a little while, but tepid for a long time; it cools faster when it’s hotter.

In a holy bucket, the higher the water level, the faster the water flows out. Differences in temperature work the same way. The greater the difference in temperature, the faster the heat flows out.
Ultimately, the amount of energy that a heater puts into the pool is equal to the heat lost from the pool. Since you lose more heat energy from a hot pool than from a cool pool, the most efficient thing you can do is keep the temperature as low as possible for as long as possible. The most energy efficient thing to do is always to turn off the heater. The only reason to keep it on is so that you don’t have to wait for the water to warm up before you use it.
It seems as though a bunch of water is a good place to store heat energy, but the more time something spends being hot, the more energy it drains into everything around it.
Answer Gravy: This gravy is just to delve into why picturing heat flow in terms of the random motion of hypothetical particles is a good idea. It’s well worth taking a stroll through statistical mechanics every now and again.
The diffusion of heat is governed, not surprisingly, by the “diffusion equation”.
The same equation describes the random motion of particles. If ρ(x,t) is the amount of heat at any given location, x, and time, t, then the diffusion equation tells you how that heat will change over time. On the other hand, if ρ is either the density of “beads” or the probability of finding a bead at a particular place (if the movement of the beads is independent, then these two situations are interchangeable), then once again the diffusion equation describes how the bead density changes over time. This is why the idea of “heat beads” is a useful intuition to use; the same math that describes the random motion of particles also describes how heat spreads through materials.
In one of his terribly clever 1905 papers, Einstein described how the random motion of individual atoms gives rise to diffusion. The idea is to look at ρ(x,t) and then figure out ρ(x,t+τ), which is what it will be one small time step, τ, later. If you put a particle down somewhere, wait τ seconds and check where it is over and over, then you can figure out the probability of the particle drifting some distance, ε. Just to give it a name, call that probability ϕ(ε).
ϕ(ε) is a recipe for figuring out how ρ(x,t) changes over time. The probability that the particle will end up at, say, x=5 is equal to the probability that it was at x=3 times ϕ(2) plus the probability that it was at x=1 times ϕ(4) plus the probability that it was at x=8 times ϕ(-3) and so on, for every number. Adding up the probabilities from every possible starting position is the sort of thing integrals were made for:
So far this is standard probability fare. Einstein’s cute trick was to say “Listen, I don’t know what ϕ(ε) is, but I know it’s symmetrical and it’s some kind of probability thing, which is pretty good, amirite?”.
ρ(x,t) varies smoothly (particles don’t teleport) which means ρ(x,t) can be expanded into a Taylor series in x or t. That looks like:
and
where “…” are the higher order terms, that are all very small as long as τ and ε are small. Plugging the expansion of ρ(x+ε,t) into we find that
Einstein’s cute tricks both showed up in that last line. since ϕ(ε) is symmetrical (so the negative values of ε subtract the same amount that the positive values add) and
since ϕ(ε) is a probability distribution (and the sum of probabilities over all possibilities is 1).
So, can be written:
To make the jump from discrete time steps to continuous time, we just let the time step, τ, shrink to zero (which also forces the distances involved, ε, to shrink since there’s less time to get anywhere). As τ and ε get very small, the higher order terms dwindle away and we’re left with . We may not know what ϕ(ε), but it’s something, so
is something too. Call that something “k” and you’ve got the diffusion equation,
.
The second derivative, , is a way to describe how a function is curving. When it’s positive the function is curving up the way your hand curves when you palm is pointing up and when it’s negative the function is curving down. By saying that the time derivative is proportional to the 2nd position derivative, you’re saying that “hills” will drop and “valleys” will rise. This is exactly what your intuition should say about heat: if a place is hotter than the area around it, it will cool off.
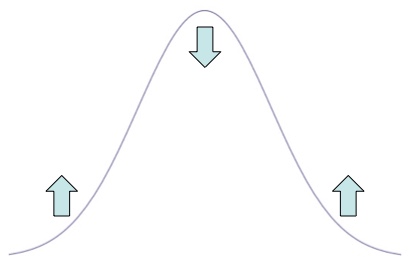
The diffusion equation dictates that if the graph is concave down, the density drops and if the graph is concave up, the density increases.
This is a very long-winded way of saying “think of heat as randomly moving particles, because the math is the same”. But again, heat isn’t actually particles, it’s just that picturing it as such leads to useful insights. While the equation and the intuition are straight forward, actually solving the diffusion equation in almost any real world scenario is a huge pain.

The corners cool off faster because there are more opportunities for “heat beads” to fall out of the material there. Although this is exactly what the diffusion equation predicts, actually doing the math by hand is difficult.
It’s all well and good to talk about how heat beads randomly walk around inside of a material, but if that material isn’t uniform or has an edge, then suddenly the math gets remarkably nasty. Fortunately, if all you’re worried about is whether or not you should leave your heater on, then you’re probably not sweating the calculus.
The shuttle tile photo is from here.