Q: How can carbon dating work on things that were never alive?

Posted on July 21, 2017 by The Physicist

Physicist: It doesn’t.

Carbon dating is the most famous form of “radiometric dating”.  By measuring the trace amounts of radioactive carbon-14 (so named because it has 6 protons and 8 neutrons) in a dead something and comparing it to the amount of regular carbon-12 (6 protons and 6 neutrons) you can figure out how long it’s been since that sample was alive.  Carbon-14 is continuously generated in the upper atmosphere when stray neutrons bombard atmospheric nitrogen (which is what most of the atmosphere is).

The reason carbon dating works is that the fresh carbon-14 gets mixed in with the rest of the carbon in the atmosphere and, since it’s chemically identical to regular carbon, gets worked into whatever is presently absorbing atmospheric carbon.  In particular: plants, things that eat plants, things that eat things that eat plants, and breatharians. When things die they stop getting new carbon and the carbon-14 they have is free to radioactively decay without getting replaced.  Carbon-14 has a half-life of about 5,700 years, so if you find a body with half the carbon-14 of a living body, then that somebody would have been pretty impressed by bronze.

Of course none of that helps when it comes to pottery and tools (except wooden tools).  Not being made of carbon, we can’t carbon date them.  Fortunately, the stuff ancient civilization leave lying around tend to be found in clumps called “middens”.  A less sophisticated word for midden is “pile of garbage and often poo”.

Archaeology.

Generally speaking, archaeologists make the assumption that if the grains in and around of a clay pot are, say, 8,000 years old, then the pot itself is roughly the same age.  Which makes sense.  If you had an ancient amphora sitting around, would you use it for fresh strawberry preserves?  And before you answer: please do it.  A life spent potentially confusing future archaeologists is a life well spent.

There are many different kinds of radiometric dating that are used to date things that are non-organic (which is part of how we determine the age of the Earth).  They each rely on a couple of different (thoroughly verified) principles.  First, that radioactive isotopes have a fixed half-life (totally independent of their environment).  And second, that the elements they were before and after the radioactive decay have different chemical properties.

As water freezes and each molecule falls into place, atoms that don’t fit in the forming ice crystal are excluded.  Impurities, such as dissolved air, are either forced out or concentrated in the last region to freeze.  The same is true for any kind of crystal.

Crystals are regular lattices of atoms.  And they’re picky.  If an atom doesn’t interact chemically in the right way, then it won’t be incorporated into a forming crystal.  For example, zircon (a crystal) is perfectly happy to incorporate uranium, but excludes lead.  It so happens that uranium decays into lead with a half-life of 4.5 billion years.  So if you grind up a zircon and measure the tiny amounts of lead vs. uranium, you’re measuring how long it’s been since that zircon formed.  At that time there would have been zero lead in it.

Since carbon-14 has a half-life on the order of thousands of years, it’s useful for figuring out the age of organic materials that have been independent of the atmosphere for thousands of years.  Since uranium-238 (the isotope comprising more than 99% of natural uranium) has a half-life of billions of years, it’s useful for figuring out the age of (among other things) zircons that crystallized billions of years ago.  Want to date a woolly mammoth?: carbon dating.  Want to date a planet?: uranium dating.

Radiometric dating generally involves tallying up trace amounts of material, so it’s not the sort of thing you do out in the field; you need a clean lab.  So it was, after years of attempting to measure the age of the Earth (or, more specifically, the time since it was last molten) in a regular lab, that Clair Patterson bravely announced “Dudes and dudettes of science… anybody else notice all the lead in the air?”  Turns out that burning gasoline, among its other little known deleterious effects, throws lead into the air.  That’s not great: once everything on Earth is peppered with lead, it’s difficult for scientists to do their science.  And, not for nothing, it’s also caused a thousandfold increase in lead contamination in the bodies (or bones at least) of everything that breathes and/or eats.  If you’ve ever wondered why gasoline should be “unleaded”: that’s why.

This is the beauty of fundamental research: you never know what you’ll find when you start poking around.

Posted in -- By the Physicist, Particle Physics, Physics | 7 Comments

Teleportation! In space!

Posted on July 12, 2017 by The Physicist

Physicist: This isn’t a question anybody asked, just an interesting goings-on.

A few weeks ago QUESS (QUantum Experiments at Space Scale) began teleporting quantum information to and from the Micius satellite and between ground stations 1200 km apart.  This is exciting, because it demonstrates the feasibility of easy (cheap), high-fidelity, long-distance quantum entanglement, which is the key to all quantum communication.  Micius is the first shaky pillar of a global-scale quantum infrastructure.

Time-lapse of a laser in Xinglong talking to Micius, the world’s first “quantum satellite”.

Entanglement is basically a combination of correlation and superposition.  The difference between a bit and a qubit is that a bit is either 1 or 0 while a qubit is simultaneously 1 and 0.  There are a lot of different forms that a qubit can take (just like there are many forms a bit can take): in this case the polarization of light is used.  There are two possible polarization states, which is perfect for encoding two possibilities, 0 and 1 (and incidentally perfect for making 3D movies; one movie for each polarization and each eye).

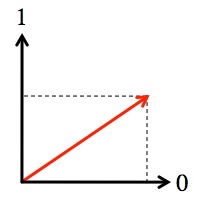
The polarization of light can point in any direction (perpendicular to the direction of travel), so we can use it to describe not just 0 or 1 but a combination of both.

A photon can be in a superposition of both horizontal and vertical polarization.  When measured they are always found to be in one state or the other (0 or 1), but there are a lot of clever things we can do with qubits before doing that measurement.

While it is impossible to be sure of the result, the probability that you see a “0” or “1” is described by the state (in the picture above, “0” is more likely, but not guaranteed).  The spooky thing about entangled particles is that, as long as you measure them the same way, their random results will be correlated.  For the simplest kind of entangled state, |\Phi^+\rangle, the results are the same.  If two photons are in the shared state |\Phi^+\rangle and you find that one of them is vertically polarized, then the other will also be vertically polarized.  Random, but the same as each other.  Unfortunately, practically any interaction with either particle breaks the entanglement and leaves you with just a pair of regular, unrelated particles.  This discussion on entanglement goes into a bit more detail.

How do you get entangled particles thousands of km apart?  Carefully.

What QUESS is doing, and what “quantum communication” is all about, is getting two entangled particles far apart without accidentally breaking the entanglement or losing the particles (which is difficult when they’re being fired at you from space).

Once two widely separated parties share a pair of entangled particles, they can start doing some rather remarkable things.  One of those is the ability to send qubits from one particle to its entangled twin: “quantum teleportation”.  Quantum teleportation requires both an entangled pair of particles and a “classical communication channel” (which includes, but is not limited to, shouting loudly).  With those in hand, we can easily “teleport” a qubit, from one location to another.

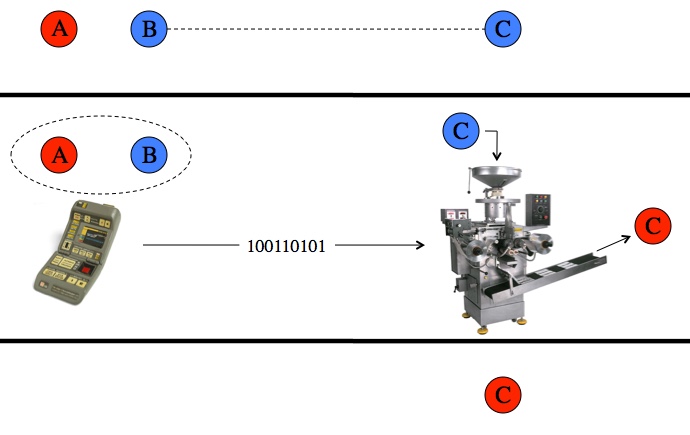
Top: One state you’d like to teleport, A, and two particles sharing an entangled state, B and C. Middle: Some relative properties of A and B are measured and the results are sent to whomever has the other entangled particle. Based on that information, the other entangled particle is manipulated. Bottom: The result is that the entanglement is destroyed, but C assumes A’s original state.

Qubits (quantum states in general) are as delicate as delicate can be.  Absolutely any interaction capable of allowing anything to determine their state “collapses” that state; a qubit goes from being both 0 and 1 to being either 0 or 1, and all of the advantages that may have gone with that superposition go out the window.  So teleportation needs to be able to measure the to-be-sent qubit, A, without actually determining anything about it, which is tricky.  The way to get around that is to do a measurement that compares A and B, without measuring either of them directly.  If you learn that two coins have either the same or opposite side up, then you’ve learned something about the two of them together, but nothing specific about either of them individually.

The same idea applies in quantum teleportation.  The central idea behind entanglement is that if B and C are entangled, then they react to measurements in the same way.  So by comparing A and B and learning how they’re different, you’re also learning how A and C are different.  Knowing that, you can figure out what needs to be done to C to make it have the same state as A.  And all without actually learning what that state is.  Even if C is, hypothetically, on the far side of China, you can just tell whoever has it what the results of the test were.  For coins/regular bits you only need to send one bit of information; the result of the comparison is either “same” or “different”.  For qubits you need to send two bits, because of how terrifyingly complex quantum mechanics is.  Here’s a bit more detail on how quantum teleportation works.

Not a lot of physicists are too surprised that ground-to-space quantum teleportation works (nobody builds and launches spacecraft on a hunch).  There’s never been any indication that distance is a factor for quantum entanglement, so this isn’t a matter of overcoming physical laws, just getting around (a lot of) engineering difficulties.  Teleportation is easy to do with equipment on opposite sides of a room.  The difference here is that the “opposite side of the room” is moving at about 8 km/s and is in freaking space.

Quantum states are delicate, so we need to be able to catch, manipulate, and accurately measure the states of individual photons with minimal interference.  Assuming that you’re not having someone else read this out loud, you are presently noticing that photons carry information through air pretty well.  Pretty well.  Over a large enough distance, even clean air is effectively opaque.  The present through-air record for this same procedure is 143 km, between a couple of Canary Islands.  That’s 143 km through the densest region of our atmosphere (sea level).  There’s about as much air between you and space as there is between you and anything 7 km away along the ground (it gets thin fast as you go up).  So teleportation straight up should be easier than teleportation between ground stations.

Generally speaking, the big problem with conveying intact quantum information is all the stuff in the way, so space is kind of an obvious solution.  The problem with space is the distances involved; the farther something is away, the smaller the target.  Establishing entanglement between two locations comes down to creating a pair of entangled particles in one location and then sending one of the pair to the other location.  QUESS manages to catch about 1 in every 6 million photon pairs and it doesn’t work during the day because the sunlight scatters off of the air (likely to be a non-issue between two quantum satellites).  In all, the QUESS team claims to be able to establish 1 entangled pair per second.  All things considered, that’s bragging-rights-impressive.  This and this is what constitutes “bragging” (the QUESS team’s official papers on the subject).

Even with a noisy channel, with lots of photons lost and the states of many of the others perturbed by their journey, a reliable quantum channel is still possible.  We can distill quantum entanglement, turning many weakly entangled pairs into fewer strongly entangled pairs.  You can think of this like repeating a digital message to get it across a noisy channel; it takes more time to send the signal, but the result is a message clearer than any of the individual attempts.  Once an entanglement has been established between two parties, a quantum state can be teleported between the two, including a state entangled with something else.  In this way, two entangled pairs between A-B and B-C can be turned into one entangled pair between A-C.  With “quantum repeaters” in place, we can establish quantum channels over huge distances by piecing together many short, possibly noisy, channels.  Point is: despite quantum states being perfectly delicate, we don’t need perfect delicacy to work with them.

In the golden age of the telegraph, we could send information (bits) anywhere, we just couldn’t do too much with them when they got there.  We’re entering a similar (but likely to be much shorter) age of quantum information.

Quantum information technology is still in its infancy.  Where we are now is analogous to the age of telegraphs and Morse code.  We can send qubits, a few at a time, over long distances, but we don’t have computers at the ends capable of doing much with those qubits.  Despite that massive shortcoming, there are some killer apps that are likely to drive this technology forward.  In particular: quantum cryptography.

Skirting the details, quantum encryption boils down to:

1) distribute lots of pairs of entangled particles

2) measure each pair the same way

3) write down the results

No quantum computation involved!  The defining characteristic of maximally entangled pairs is that measurements on the pair are perfectly correlated and fundamentally random.  Anyone/thing that intercepts an entangled particle breaks (or at least weakens) the entanglement, so eavesdropping can be detected.  For you cypherpunks out there, quantum cryptography is a method of creating a shared random secret that is perfectly robust to man-in-the-middle attacks (or at least detects such attempts).  You and someone else create a random number that only the two of you can possibly know, which allows you to then encrypt any message and send it (by email for example) with security guaranteed by physical laws.

Quantum cryptography: sharing and securing secrets with fundamental physics!

Shockingly, this is of interest to lots of space-capable governments, so Micius is unlikely to be the last quantum communication satellite.

Just as a quick aside, since it’s often not stated clearly: quantum teleportation does not involve actual teleportation in any sense.  Nothing actually makes the journey from one quantum system to the other.  There are a pair of theorems in the field of quantum information theory that say that if you and someone else share an entangled pair of particles (sometimes called an “ebit”), then at the cost of that entanglement and the application of some cute tricks you can:

1) send 2 bits to convey one qubit

2) send 1 qubit to convey two bits

The first procedure is called “teleportation” and the second is called “super-dense coding”.  One of those is a terrible, misleading name and the other is “super-dense coding”.

The laser picture is from here, the telegraph picture is from here, and the spy picture is by Tomer Hanuka.

Posted in -- By the Physicist, Entropy/Information, Physics, Quantum Theory | 18 Comments

Q: If the world is a giant magnet, how come we can’t build a repelling magnet that can float?

Posted on July 8, 2017 by The Physicist

Physicist: Three big reasons:

1) The Earth’s magnetic field is hella weak

2) it’s so big and roughly uniform that there’s no reason for a magnet to go one direction or the other

3) floating a magnet in a magnetic field is a delicate balancing act even in the best circumstances.

It turns out that it’s important to keep track of more than just polarity (north/south attract, north/north and south/south repel).  To understand how magnets behave in a magnetic field you also need to consider gradient: the direction in which the field gets stronger and how fast it gets stronger.

“A magnet” or “magnetic dipole”.

Neodymium magnets (the silver ones that seem like no big deal now, but are really impressive to magnet enthusiasts who grew up with those brittle black magnets back in the day) can support a magnetic field as high as a little over 1 Tesla at their surface.  Earth’s magnetic field is on the order of 1 ten thousandth as strong at its surface.  If you had an electromagnet with the strength of the Earth’s magnetic field, you’d barely be able to pick up paper clips with it.

You might be able to make up for the weakness of Earth’s magnetic field by making your magnet ridiculously strong (somehow), but you’ll quickly run into the second big issue: uniformity.  A uniform magnetic field doesn’t attract or repel magnets, it turns them until they line up.

Placed in a uniform magnetic field a magnet won’t move, but it will rotate to align with that field.

If you have a bar magnet, it’s north and south poles are both basically the same distance from either of the Earth’s poles.  As much as one is pulled, the other is pushed just as strongly.  That’s why compass needles line up with the Earth’s field, but otherwise stay put.  Unfortunately, there’s no way to get a magnet that’s “just north“.  Magnets always come in north/south pairs, so you’ll never get a magnet that simply moves in the direction of the magnetic field.

Fortunately for magnetophiles, physics is complicated.  You may have noticed that a pair of magnets will attract (after aligning with one another).  Despite both of them having a north and a south which will attract and repel one of the poles in the other magnet, a pair of magnets will still manage to attract each other overall.  This is because when the field drops rapidly with distance the pull the closer pole feels is greater than the push that the farther pole feels.  In mathspeak, if the magnetic moment of your magnet is \mu and the external field is \vec{B}, then the force on the magnet is \vec{F} \approx \left(\vec{\mu}\cdot\nabla\right)\vec{B}.  The “magnetic gradient” points in the direction in which the strength of the magnetic field increases the fastest (typically, toward the source of the field) and it is bigger for magnetic fields that change quickly over a given distance.  The bigger the gradient, the bigger the total pull (or push) on a magnet.  The Earth’s magnetic gradient is very small because it’s field doesn’t change very fast; if you move a mile in any direction right now, you’ll find the Earth’s magnetic field will be about the same.

So when subjected to a magnetic field a magnet will first rotate to line up and then move toward the strongest part of the field (“in the direction of the gradient”).  If you’re dealing with two magnets, the field is typically strongest at the location of the other magnet, so pairs of magnets tend to snap together.  Were you so inclined, you could figure this out directly by thinking about magnetic dipoles in terms of current loops (a standard way to do things in physics) and then applying Maxwell’s laws.

The lower current loop (simple magnet) is attracted to the region with the strongest external magnetic field.  Ultimately, this is why magnets attract each other.

Genuine magnetic levitation is a subtle art.  Earnshaw managed to figure out that there is no way to hold a magnet fixed in space using other magnets.  There a couple of cute exceptions which, by and large, are not helpful in the case of levitating in Earth’s magnetic field.

Left: Diamagnetic water floating in the weakest (but still very strong) part of a magnetic field. Middle: A gyro-stabilized magnet in a peculiarly-shaped field.  Right: A regular magnet held in place by the super-conducting puck below it.

Some materials have properties that only show up in very strong fields.  In particular, diamagnetic stuff (such as water) will flee to the region with the weakest field, which can be in open space.  But this typically requires a field on the order of a hundred thousand times the strength of Earth’s, confined to a very small region.  For only several million dollars we can levitate frogs (and also do important fundamental research or whatever).  This isn’t helpful because it requires both a big magnetic gradient and a powerful field.  Even for the most extreme diamagnetic materials, Earth’s field falls well short.

The “carefully crafted” field needed to levitate a magnetic top.

You can also violate Earnshaw’s theorem by removing the “fixed” requirement.  Levitating tops want to flip over and fly toward their magnetic base, but as long as they’re spinning in a properly shaped field, they’re gyro-stabilized.  If the top starts to tip, gyroscopic forces cause its axis (which points in the same direction as its magnet) to tip in such a way that it is pushed upright and back to the middle.  It is not immediately obvious why, but interesting nonetheless.  This sort of levitation requires a very particularly crafted, hourglass-shaped, magnetic field (again, with a large gradient).  Not at all like Earth’s.

Type II superconductors expel magnetic fields but, if forced, they’ll allow the field through in “flux tubes”.  The greater the field, the greater the number of tubes.  It takes a little energy to create or destroy each tube, so superconductors like to keep the field fixed (typically by not moving).  Excitingly, if a nearby region has the same magnetic field, then a superconductor can easily “slide” into it.

Superconductors come in a few different flavors, but the most common are type II (typically written “type II” rather than “type 2”, because physicists like to be fancy).  Type II superconductors are, for lack of a better word, “grumpy” about magnetic fields.  They expel magnetic fields from their interiors, but if you force them to be in a field (using advanced techniques such as “putting them there with your hand”), then the magnetic field lines will instead pierce through the material in tiny tubes.  In this case, rather than expelling them, the material refuses to let the magnetic field change (“Fine…  Good…  That’s exactly how I wanted the field to be.”).  It takes a little energy to create, destroy, or move these “flux tubes” so the superconductor finds itself “pinned” to the magnetic field.  Hence the name: “flux-pinning“.

But a magnetic field is a magnetic field; there’s nothing special about the field in any given place.  If the field is translationally symmetric (if you move in some direction and the field is about the same), then a floating superconductor will be free to slide in that direction.  For example, they’re able to move along tracks (friction free!) because one section of track generates the same field as the next section of track.

Even if we could build a really big “superconductor ship” and pin it to the Earth’s field, we can expect that it wouldn’t float except, perhaps, in a few very particular places.  Generally speaking, the level curves of the Earth’s magnetic field (the surfaces where it has constant strength) intersect the surface.  Ideally, we’d need the magnetic field to increase vertically (the level curves would be horizontal) so that vortex pinning would cause a giant superconductor to maintain altitude.

Best case scenario (assuming you could work with both the tiny field and the tiny gradient), a superconductor ship would experience these level curves as nested invisible walls in space that typically intersect the ground.  Worse, these “walls” aren’t terribly smooth; the Earth’s magnetic field is lumpy and variable.  You could expect your ship to constantly have to force its way through Earth’s field’s ever-varying shape.

The strength of Earth’s lumpy magnetic field.

Without some method for sliding up those “walls”, trying to use superconductors to float in Earth’s magnetic field is mostly just a way of restricting movement across Earth’s surface.  But by the time you’re doing that, you might want to consider any of the many better alternatives to levitation.

Better alternatives.

Given the methods we have for magnetic levitation, the Earth’s magnetic field is severely lacking.

The “loops in a magnetic field” picture is from here.

The “carefully crafted magnetic field” picture is from here (along with a brief discussion of how those things work).

Posted in -- By the Physicist, Engineering, Physics | 3 Comments

Q: How can something have different amounts of energy from different points of view?

Posted on June 21, 2017 by The Physicist

The original question was: … in a scenario with two cars driving towards each other, the system could be measured externally to have an energy equal to the sum of the kinetic energy in the two cars. However, if you are in one of those cars, you would see the other car moving towards you at twice the speed you are traveling, and that you are not moving at all. If that is the case, then calculating the energy in the system means instead of summing the energy of two cars moving, you have one car moving at twice the speed, which means four times the energy of one car and twice the energy of the original system.  How is it that from one perspective, a system can have twice as much energy?

Kinetic energy is given by E=0.5mv2.  With a little math you’ll find that different perspectives of the same event result in different amounts of total energy.

Physicist: When you hear about the conservation of energy it’s natural to think of it as being something like the “conservation of chairs”: there is a total and that total never changes.  But while differently moving observers will agree on chair count, they’ll disagree on how fast those chairs (and everything else) are moving.  Velocity is subjective and therefore everything that depends on velocity is also subjective.  Including energy.

Most of the physical laws we’re taught only work in the context of “inertial reference frames” (“reference frames” for short), which is just a point of view that’s moving at a constant speed.

The chess pieces behave normally (as though they were sitting still) because they’re in an Inertial Reference Frame; traveling in a straight line at a constant speed.

Chief among those laws is the conservation of energy, which rightly says “energy can neither be created nor destroyed”.  If you get a nice rock upon which to sit and watch the universe forever, you’ll find that this law holds up: if you total up the amount of energy everywhere, that value never changes.

But the conservation of energy operates on a frame-by-frame basis, not between frames.  Someone else, drifting past at a fixed velocity, will agree that the total energy stays the same, they’ll just disagree about what that total is.  That is to say, the amount of energy in a system changes (only) when you change reference frames.  For example, if you suddenly start walking the kinetic energy of the Earth jumps tremendously (it’s a planet moving past you at walking speed).

If you’re at rest with respect to the Earth, it has no kinetic energy (never mind its rotation).  But if you’re moving, even a little, you’ll see it as having a huge amount of kinetic energy.

But clearly, very few of us are gods.  Your decision to walk across a room doesn’t induce the rest of the universe to suddenly gain and then lose energy.  The situation ultimately boils down to perspective.  When you turn your head to the right you’ll notice that, miraculously, those things that were once to your right are now in front of you whereas those things that were once in front of you are now to your left.  It’s not that the universe changes, it’s that your point of view changes.

The most that you can swing the universe around at a moment’s notice.

In this sense velocity is very much like direction or position; when you change your point of view a lot of physical things change relative to you, but that doesn’t mean that they’ve physically changed.  Asking “how do other things get new energy when I change my speed?” is a lot like asking “how do things move in front of me when I turned my head?”.  Unfortunately, the same math is used to describe both physical changes (a thing actually moves) and reference frame changes (a thing appears to move because you moved), so physicists need to take pains to keep track of which is which.

The closest you can come to an “objective measure of energy” of a system is the minimum, which you see when you’re at rest with respect to the system’s center of mass.  But even that’s pretty artificial.  It’s the answer to the question “how much energy does this thing have when it’s sitting still?”.  You could just as easily say that the only “objective distance” to any given thing is zero: the distance you measure when you’re standing next to it.

If you find yourself in the enviable position of doing physics, you generally want to pick a particular reference frame and stick with it until you’ve calculated what you’re going to calculate.  That way you can use conservation of energy and momentum at will.  It doesn’t matter which reference frame you pick, just that you stick to the same one throughout.  The energy may be different, but the physical predictions about what happens will be exactly the same.

Answer Gravy: The beauty of “advanced” physics, like Relativity, is that it allows you to recast complicated things as simple.  This is a big part of how physicists pretend to be smart.

I’m about to use linear algebra which uses buckets of matrices.  While there is a lot to learn about them, it takes <5 minutes to learn the basics behind how to use one.

First, consider momentum.  When you rotate yourself the direction of a momentum vector changes, but the length, |\vec{p}|^2 = p_x^2+p_y^2+p_z^2, stays the same.  A rotation by angle \theta in the x-y plane is described by R=\left(\begin{array}{ccc}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{array}\right).  These rotations look like R:(p_x,p_y,p_z)\to(p_x^\prime,p_y^\prime,p_z).  If this were the only kind of rotation you had access to, it would be reasonable to believe that there are two conservation laws, one for the x-y plane (since (p_x)^2+(p_y)^2 = (p_x^\prime)^2+(p_y^\prime)^2) and one for the z-direction (since p_z is unchanged).

At least until someone comes along and points out that if we include the z-direction we can write that rotation as \left(\begin{array}{ccc}\cos(\theta)&-\sin(\theta)&0\\\sin(\theta)&\cos(\theta)&0\\0&0&1\\\end{array}\right).  Suddenly x-y rotations are just a special case of a more general set of rotations (which include x-z, y-z, and any combination thereof).  Even better, the z-direction ceases to be special.  Which is good!

Something similar happens to energy when you lump the time “direction” in with the other dimensions.  In the hazy days of Newtonian physics we knew all about conservation of momentum and independently the conservation of energy.  Although, technically Newton only discovered the conservation of momentum; it took Émilie du Châtelet to figure out that kinetic energy is a thing, which is much more impressive.

Einstein, being clever, found a way to describe space and time together and in the process combined both conservation laws into one: the conservation of 4-momentum, p^\nu.  Kinetic energy is literally the time-component of the 4-momentum: p^\nu = \left(\frac{E}{c},p_x,p_y,p_z\right).  That “c” is the speed of light.  Try not to notice it.

That same x-y rotation can be done in 4-dimensional spacetime using \left(\begin{array}{cccc}1&0&0&0\\0&\cos(\theta)&-\sin(\theta)&0\\0&\sin(\theta)&\cos(\theta)&0\\0&0&0&1\\\end{array}\right).  In Relativity, moving into a new reference frame (changing your velocity) is essentially a rotation, called a “boost“, between t and a spacial direction.  It not quite the same (time is different after all), but it’s remarkably similar.

Suddenly moving in the x direction at a fraction \beta of light speed “boosts” the world using \left(\begin{array}{cccc}\gamma&-\gamma\beta&0&0\\-\gamma\beta&\gamma&0&0\\0&0&1&0\\0&0&0&1\\\end{array}\right), where \beta=\frac{v}{c} and \gamma=\frac{1}{\sqrt{1-\beta^2}}.  Just to really beat you over the head with the parallels, physicists will sometimes write this as \left(\begin{array}{cccc}\cosh(\xi)&-\sinh(\xi)&0&0\\-\sinh(\xi)&\cosh(\xi)&0&0\\0&0&1&0\\0&0&0&1\end{array}\right).

Ordinary rotations leave the magnitude of ordinary momentum, |\vec{p}|, fixed.  The amount of momentum pointing in (for example) the x-direction, p_x, can change, but |\vec{p}|^2=p_x^2+p_y^2+p_z^2 always stays the same.

Boosts leave the magnitude of 4-momentum, |p^\nu|, fixed.  The amount of 4-momentum that points in the time-direction, \frac{E}{c}, can change, but the magnitude of the 4-momentum stays the same.  Here the difference between regular geometry and spacetime geometry makes itself very apparent.  The length of the 4-momentum, p^\nu = \left(\frac{E}{c},p_x,p_y,p_z\right), is given by \left|p^\nu\right|^2 = -\left(\frac{E}{c}\right)^2 + p_x^2+p_y^2+p_z^2.  Why is that first term negative?  Because time is weird.  In fact, it is exactly that weird.

This is a really terse and totally insufficient summary of boosts and 4-momentum.  The point is: just like velocity, energy is subjective and changes in very much the same way that the direction of velocity changes when you turn your head.  Not exactly the same (because time is weird), but the difference basically boils down to some extra c’s and negative signs.

Posted in -- By the Physicist, Physics, Relativity | 29 Comments

Q: Where is the middle of nowhere?

Posted on June 13, 2017 by The Physicist

The original question was: Is there any location in intergalactic space which is so far away from anyplace that it would be impossible to see anything with normal naked eye vision?  No stars, but no galaxies, no nothing — just an empty void in all directions?

In other words, the middle of nowhere — the loneliest place in the universe.

Physicist: Yup!  A bunch of them.  They’re called cosmic voids.

The matter in our universe arranges itself in huge sheets and filaments of galaxy clusters wrapped around vast empty bubbles, like bread or a sponge.  Even inside of galaxies space is almost completely empty; on the order of 1 atom per cubic centimeter and a star every few lightyears.  But in the void between those galaxies, there is as close to nothing as you will ever find.  The largest voids are on the order of a billion lightyears across.

A map of the fairly-local universe: stuff within about half a billion light years in every direction.  Our galaxy is in the center of this map, but the scales here are so large that each dot is a cluster of many galaxies.

Only folk inside galaxies get starry skies, so the sky in every direction around you would boast a distinct lack of stars.  But the question remains: could you see the galaxies that make up the walls of the void?  Fortunately, the legwork (eyework?) for determining what is and isn’t visible to the naked eye has been done.  Using naked eyes.

In the 1770’s comet-hunting was a hip thing for the telescope-wielding wealthy of Europe to do.  Messier (who pronounced his name “Messy A”, because he was French) was tired of getting excited about the same set of barely-visible blurs night after night, so he wrote down everything he could see that definitely was not a comet and where it could be found.  Incidentally, Messier did find some comets, but those discoveries are completely forgettable compared to his list of things you can see.  The Messier Objects are are not stars, not comets, and not moving.  That leaves a lot of stuff, all of which looks like a smudge or wisp of cloud, including: nebulae (“giant space smoke”), globular clusters (dense knots of stars of our galaxy), and farthest away, nearby galaxies.

M42, The Orion Nebula, is 1300 light years away (well inside of our galaxy).  This appears about twice the size of the Moon in the sky and can easily be mistaken for a cloud.  Just so you can find it: this picture is the sword in the Orion constellation.

The most distant galaxy visible to the naked eye is about 68 million light years away and fifty-eighth on Messier’s list: the ingeniously monikered  M58.  So, about 70 million lightyears is a reasonable upper-limit to how far away a galaxy can be seen by a person.

M58, a galaxy about 68 million light years away, appears to be about a sixth the size of the Moon in the sky.  Under ideal circumstances it’s just barely visible to the naked eye as a tiny smudge.

Cosmic voids aren’t perfectly empty, just a lot emptier than the galaxy-laden regions of the galactic filaments.  There is still the occasional “rogue galaxy” to be found drifting about.  If you were in the middle of a void, and you turned off all the lights in your spaceship to let your eyes really adjust to the dark, you might be able to see the faintest smudge or two marring the black around you.  If you had a reading-light on, you wouldn’t be able to see anything at all.

Our understanding of cosmic voids is growing rapidly, but there’s still a hell of a lot to learn.  The base problem with astronomy has always been depth (i.e., the sky looks like it’s painted on a dome).  A century ago we didn’t even know that other galaxies existed because we couldn’t tell the difference between globular clusters (dense groups of stars in our galaxy) and other galaxies (groups of stars explicitly not in our galaxy).  Now we’re faced with a more subtle difficulty: it can be difficult to tell if a given galaxy is in the middle of a void or on the edges.  An error of 5%-20% in the distance is not unusual on intergalactic scales and that can make it very difficult to determine exactly how empty a given void is.

If you were meandering about in the middle of a Cosmic Void, then you might perceive, at the very edge of your ability to see and under the best conditions, some of the galaxies in the walls of the void or the rare few in the void with you.  The universe would appear to you as the interior of a hollow obsidian sphere, with a couple fingerprint smudges here and there.

This isn’t part of the question, but worth pointing at: where we are in the cosmic web.

Posted in Astronomy, Physics | 14 Comments

Q: If light is a wave, then what’s doing the waving?

Posted on May 8, 2017 by The Physicist

Physicist: In short: nothing.  Light acts like a wave, but unlike sound waves, light isn’t a material that’s moving back-and-forth.

Waves are a coordinated movement of atoms.  A wave itself isn’t made of anything, it’s just a propagating motion through a material.  Each part of the medium more or less stays where it is, but passes the movement of the wave to nearby material.

A wave is a coordinated movement that passes through a medium, generally without the medium itself moving very far.

For example, sound manages to move get from whatever-that-was-just-now to your ear at about 0.2 miles per second.  At yet, the air around you doesn’t noticeably move anywhere when sound moves through it.  Sound is literally just atoms in air smacking into other atoms, making those freshly smacked atoms move a tiny distance to smack into another set of atoms, and so on.

While waves take several different forms, the basic idea is always the same: waves are tiny movements that propagate from place to place inside of a host material.  Sound is waves in air, ripples are waves in water, earthquakes are waves in the ground; every wave seems to need some material to do the waving.

In the double slit experiment light exhibits wave-interference.  So light must be a wave.

A few centuries ago, Thomas Young proved that light is definitely a wave by demonstrating that it is capable of interference.  In so doing he also managed to measure the wavelength of visible light: 400nm for purple to 700nm for red.  Technically, what Young did was demonstrate that, whatever light it is, has wave-like properties.  At the time, everything that was known to be wave-like was in fact a wave.  So Young’s experiment led to the completely natural, titular question of this post: if light is a wave, then what’s doing the waving?

Physicists, never shy to name things they’re pretty sure exists, declared that the material light moves through is the Luminiferous Aether (“luminous” for “light” and “aether” for “I don’t know what it is either”).

Typically, when you can hear, you can breathe, and when you can be pushed by an ocean wave, you’re already wet.  Because we can see, we must be immersed in the Luminiferous Aether (otherwise, how does the light get to our eyes?).  It would seem that one of the important properties of the Aether is that you can’t feel it, see it, or smell it.

One of the first experiments concerning the Aether was to evacuate (pull all the air out of) a glass jar and look through it.  Turns out: light doesn’t need anything made of matter to move through.  The Aether must be fill the universe and pass freely through every material thing.  And since we can see stars just as clearly in every direction, it must fill the universe in a very smooth and uniform way.  Strange stuff.

There is a long history of debate over why the Aether does or doesn’t exist.  It doesn’t.  Here’s a very brief thread of the debate that more or less gets to (one of) the heart(s) of the issue.

The fact that light has polarization means that it is a transverse wave (side/side), but only longitudinal waves (forward/back) can exist in a gas or liquid.

a: Longitudinal waves can exist in gases.  b: Both longitudinal and transverse waves exist in solids.

That implies that the Aether must be a solid that permeates all of space.  But here’s the thing: Earth moves.  More than that, it moves in big circles, so for most (if not all) of the year it must be moving relative to the Aether.  That movement is detectable.

If you drop pebbles off of a moving boat, you’ll notice that the ripples moving toward the front of the boat move slower and the ripples moving toward the back move faster (from your boat-bound perspective).  If you bounce waves back and forth in a moving medium you find that they go faster in one way and slower in the other and that overall the slow part “wins”; waves always take longer to go out and come back in a moving medium.  So bouncing waves back and forth is a good way to tell if you’re moving and even how fast.

Enter Michelson-Morley.  In the late 19th century they created an interferometer which bounced light back and forth in two directions and then compared the two paths.  Any discrepancy in the direction or speed of the waves in either direction is immediately detectable.  I’m mean, you can’t even breathe near these things without sending the interference pattern into convulsions.  In fact, interferometers are so sensitive that they’re used to detect gravity waves (which are a really, really… really tiny effect).

Left: In an interferometer light is bounced along two paths and recombined.  Right: The combined light interferes creating an interference pattern.  These are infamously sensitive to even tiny changes.

But no matter how Michelson and Morley aligned their apparatus, and no matter how it was moving, the results were always exactly consistent with zero movement of the Aether.  So assuming it exists, the Aether must be solid and it must be stationary with respect to the Earth.  This spawned a whole string of weird theories, like that the Aether is mostly solid but also sticks to the Earth as it moves.  These new theories have since been ruled out one by one.  For example, if the Earth did have a blob of Aether stuck to it, the “shear boundary” between the Earth’s moving patch of Aether and the differently moving Aether of deep space should have made stars appear to move throughout the year.  But they don’t.

Following light, we found that every other kind of quantum wave (there’s one for every different kind of particle), has wave-like properties but no medium.  For example, electrons are also waves and they also don’t need a medium to move through (they move through deep space all the time).  These mediumless-waves are distinct from the waves we’re usually talking about when we say “wave” (like sound and ripples).  We need a new word for mediumless-waves to distinguish them from mediumful-waves.  “Evaw” maybe?  Or… anything other than Evaw.

Posted in -- By the Physicist, Experiments, Physics | 38 Comments