Physicist: If you wait forever, then you might see something happen. But the more practical answer is: no.
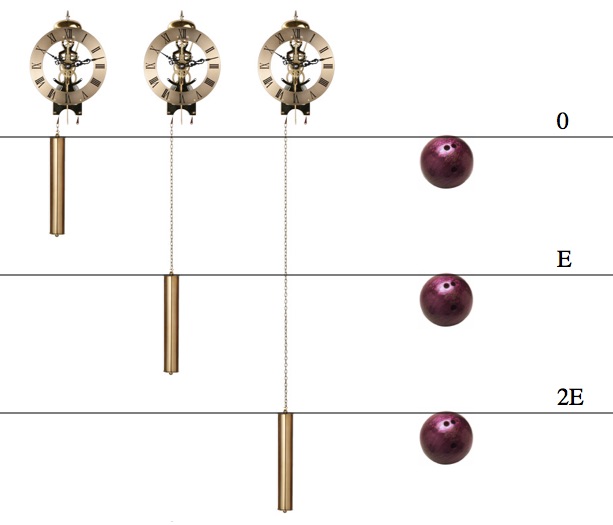
The universe does a lot of stuff (for example, whatever you did today), but literally everything that ever happens increases entropy. In some sense, the increase of entropy is equivalent to the statement “whatever the most overwhelmingly likely thing is, that’s the thing that will happen”. For example, if you pop a balloon there’s a chance that all of the air inside of it will stay where it is, but it is overwhelmingly more likely that it will spread out and mix with the other air in the room. Similarly (but a little harder to picture), energy also spreads out. In particular, heat energy always flows from the hotter to the cooler until everything is at the same temperature (hence the name: “thermodynamics”).
If you get in front of that flow you can get some work done.

All machines need to be between a “source” and a “sink”. If the source and sink are at the same temperature, then there’s no reason for energy to flow and the machine won’t work. For example, if the water were already steam (not previously cold), then it won’t expand and you can’t use it to do work.
“Usable energy” is energy that hasn’t spread out yet. For example, the Sun has lots of heat energy in one (relativity small) place. Ironically, if you were in the middle of the Sun, that energy wouldn’t be accessible because there’s nowhere colder for it to flow (nearby).
The spreading out of energy can be described using entropy. When energy is completely and evenly spread out and the temperatures are the same everywhere, then the system is in a “maximal entropy state” and there is no remaining useable energy. This situation is a little like building a water wheel in the middle of the ocean: there’s plenty of water (energy), but it’s not “falling” from a higher level to a lower level so we can’t use it.

Useable energy requires an imbalance. If all the water were at the same level there would be no way to use it for power.
The increase of entropy is a “statistical law” rather than a physical law. You’ll never see an electron suddenly vanish and you’ll never see something moving faster than light because those events would violate a physical law. On the other hand, you’ll never see a broken glass suddenly reassemble, not because it’s impossible, but because it’s super unlikely. A spontaneously unbreaking glass isn’t physically impossible, it’s statistically impossible.
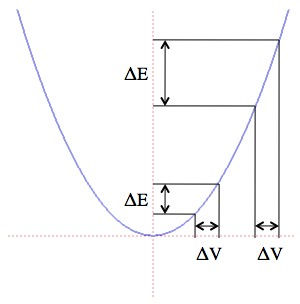
However, when you look at really, really small systems you find that entropy will sometimes decrease. This is made more explicit in the “fluctuation theorem“, which says that the probability of a system suddenly having a drop in entropy decreases exponentially with size of the drop.
For example, if you take a fistful of coins that were in a random arrangement of heads and tails and toss them on a table, there’s a chance that they’ll all land on heads. That’s a decrease in the entropy of their faces, and there is absolutely no reason for that not to happen, other than being unlikely. But if you do the same thing with two fistfuls of coins it’s not twice as unlikely, it’s “squared as unlikely” (that should be a phrase). 10 coins all landing on heads has a probability of about 1/1,000, and the probability of 20 coins all landing on heads is about 1/1,000,000 = (1/1,000)2. The fluctuation theorem is a lot more subtle, but that’s the basic sorta-idea.
The “heat death of the universe” is what you get when you starting talking about the repercussions from ever-increasing entropy and never stop asking “and then what?”. Eventually every form of useable energy gets exhausted; every kind of energy ends up more-or-less evenly distributed and without an imbalance there’s no reason for it to flow anywhere or do work. “Heat death” doesn’t necessarily mean that there’s no heat, just no concentrations of heat.
But even in this nightmare of homogeneity we can expect occasional, local decreases in entropy. Just as there’s a chance that a broken glass will unbreak, there’s a chance that a pile of ash will unburn, and there’s a chance that a young (fully-fueled) star will accidentally form from an fantastically unlikely collection of scraps. There’s even a chance of a fulling functioning brain spontaneously forming. But just to be clear, these are all really unlikely. Really, really unlikely. As in “in an infinite universe over an infinite amount of time… maybe“. We do see entropy reverse, but only in tiny quantities (like fistfuls of coins or the arrangements of a few individual molecules). Something like the air on one side of a room (that’s in thermal equilibrium) suddenly getting 1° warmer while the other gets 1° colder would literally be the least likely thing that’s ever happened. The universe suddenly “rebooting” after the heat death is… less likely than that. Multivac interventions notwithstanding.
Those events that look like decreases in entropy have always been demonstrated to be either a matter of not taking everything into account or just being wrong.

Fun fact: Patents for perpetual motion machines are the only patents that require a working model. Yet another example of the scientific conspiracy at work!
Long story short: yes, after the heat death there should still be occasional spontaneous reversals of entropy, but they’ll happen exactly as often as you might expect. If you break a glass, don’t hold your breath. Get a new glass.