Physicist: Freaking terrible.
The Enigma machine used a “rolling substitution cypher” which means that it was essentially a (much more) complicated version of “A=1, B=2, C=3, …”. The problem with substitution cyphers is that if parts of several messages are the same then you can compare their similarities to break the code. Enigma was broken in part because of German formality (most messages started with the same formal greeting). Even worse, since some letters are more common than others (e.g., “e” and “g”) you can make progress by just counting up how often letters show up in the code (or even get an idea of what language the code is written in without breaking it!). Substitution cypher are so easy to break that some folk do it for fun. Rolling substitution cyphers can use a set of several encoding schemes and cycle through which code is used or make the scheme dependent on the previous letter, but this merely makes the code breaking more difficult. Ultimately, all substitution cyphers suffer from the same difficulty: similar messages produce similar looking codes.
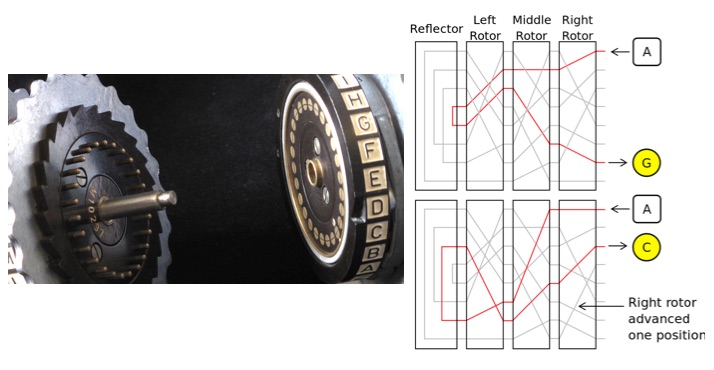
Enigma used three rotors which rotated after each letter was pressed allowing them to generate a huge number of different substitution cyphers, using a different one for each letter. Still: what your cellphone uses is much, much better.
Modern cryptography doesn’t have that problem. If any part of a message is different at all, then the entire resulting code is completely different from beginning to end. That is; if you encrypted a message, you’d get cypertext (the encoded message) and if you were to encrypt the exact same message but misspelled a single word, then the cypertext would be completely different.
If your messages were “Hello A”, “Hello B”, and “Hello C”, then a substitution cypher might produce “Tjvvw L”, “Tjvvw C”, and “Tjvvw S” while RSA (the most common modern encryption) might produce “idkrn7shd”, “62hmcpgue”, and “nchhd8pdq”. In the first case you can tell that the messages are nearly the same, but in the second you got nothing.
Enigma was very clever but is shockingly primitive compared to modern crypto techniques. If anyone in WW2 had been using modern (1970’s or later) encryption, then there is no way that anyone would have been able to break those codes (and Turing would have to settle for being famous for everything else he did).
There’s a post here that talks about the main ideas behind RSA encryption. The really fancy stuff is some of the only math that isn’t publicly known. Scientists have a whole thing about openness and the free exchange of information that governments and corporate entities (for whatever reason) don’t.