Ask a Mathematician / Ask a Physicist

Q: Is getting plasma really hot the only way to initiate fusion?

Posted on September 30, 2020 by The Physicist

Physicist: No. But for all practical purposes, yes.

“Fusion” is a pair of atoms coming together and fusing (hence the name) into a single, larger atom. In a chemical bond, like hydrogen and oxygen linking up to form water, the electrons around the nuclei interact with each other. In fusion the nuclei themselves are brought together and in the process a truly fantastic amount of energy is released (for elements lighter than iron). Sadly, it takes some rather extreme circumstances to get nuclei to touch.

As any physicist or marriage counselor can tell you: opposites attract and likes repel. This is about the electrical force on electrical charges and the fact that when you date someone like yourself, you’re dating someone like your least favorite parent. In the nucleus of every atom are positively-charged protons, which packs a lot of positive charge in a very small place and makes it very hard to bring two nuclei together. But if you can get those nuclei close enough, the “nuclear strong force” (so named because it only applies to the stuff inside the nucleus and is, in fact, strong) overwhelms the repulsion and snaps the nuclei together. So the name of the game is getting nuclei close enough for the strong force to take over. But that’s not easy.

To get fusion happening, you get a heck of a lot of hydrogen atoms and just slam them together over and over; the nuclear physics version of winning skeeball with a trash can full of wooden balls. Once hydrogen is heated to above around ten million degrees C, it’s moving fast enough to overcome the repulsive force and very, very occasionally fuse (anyone who’s played around with strong magnets can attest to the fact that if you don’t bring them together square-on, they’ll “slip” off each other and fly apart sideways). The Sun’s core, famously a hotbed of nuclear fusion, is only barely capable of fusion despite its hydrogen being a toasty 15,000,000°C and crushed by the weight of the star above it to twenty times the density of solid iron. The rate of fusion in the Sun is so slow that a person-sized chunk of the core produces heat at about the same rate your body does. The Sun shines because the core is a lot bigger than you, so even that trickle of fusion adds up to a lot. Meanwhile, here on Earth, we use a far more efficient form of fusion.

H-Bombs: briefly more efficient than the Sun.

In fusion weapons we strive to get as much hydrogen to fuse as possible, as quickly as possible, which means temperatures and pressures much greater than the core of the Sun. The “easiest” way to do that is to get a big brick of lithium hydride (which, weirdly enough, has a hydrogen density 50% greater than liquid hydrogen) and surround it with fission bombs to squeeze and heat it. The issue with this method of harnessing fusion power is… existential. An electrical power plant only works when you don’t blow it up. Considering that hydrogen is far and away the most abundant stuff in the universe (and we have oceans of it here on Earth in the form of oceans) and fusion is the greatest potential power source humanity has ever tapped, it would be really nice if we could come up with a way to fuse hydrogen that wasn’t so hot, dense, and explosive. A sort of cold fusion, if you will.

Unfortunately, that’s just not possible with hydrogen. The simple fact is that a pair of free protons zipping around in a plasma (hot hydrogen) are just too good at repelling each other. That colossal heat is necessary for them to get the kind of speed they need to run up the ramp of their mutual repulsive potential and (at least sometimes) get close enough for the strong force to grab them. Ironically, getting close is easier for cold hydrogen gas because each proton carries an electron with it, instead of all of them flying about wildly in a plasma.

A charge looking at a “neutral atom” sees the same amount of positive charge as negative charge, so there’s no net attraction or repulsion for any charges. That balance of charge is, in a nutshell, why you don’t experience literally Earth-shattering electrical forces all the time. Completely strip the electrons from just two grams of matter and place those two grams on opposite sides of Earth, and they’d still be pushing each other so hard you’d need a little over fifty tonnes of force on each to keep them from moving even farther apart. The electric force is bonkers strong and the only reason that matter doesn’t instantly tear itself apart is that all of its charges are perfectly (or very nearly) balanced.

The repulsive force between protons still exists, but only between the nucleus (where all the positive charge is) and the electron cloud that surrounds it (where all the negative charge is). Outside of the electron cloud the positive charge is “shielded” and the electric field is effectively zero; there’s a positive charge and a negative charge right next to it, so they push and pull the same amount in the same direction and cancel each other out.

On the face of it, it would seem that that’s that. If you have neutral hydrogen, then it’s cold and its atoms won’t be slamming into each other hard enough to fuse, and if you have a plasma it needs to be middle-of-a-star hot or hotter. That’s not to say that it can’t be done. There is very active and promising research going on into fusion power, it’s just not cold fusion (and that’s what the question is about).

An active tokamak fusion reactor, using magnets to control and compress plasma. Although systems like this have yet to produce more energy than it takes to run them, they’re getting close. Please note that this is not some sci-fi picture; it’s from a camera pointed through a tiny window into an extremely hot and very unpleasant room.

It just so happens that the electron has a couple of “cousins”, the much heavier muon (~207 electron masses) and the much, much heavier tauon (~3,477 electron masses). Both decay to electrons, but muons take entire millionths of a second to do so (which, for particle physicists, is practically forever).

Muons can orbit atomic nuclei just like electrons do, forming “muonic hydrogen” (for millionths of a second), but their higher mass makes them orbit much closer. This fact is a gorgeous example of the wave nature of matter. As with light, higher energy means higher frequencies and shorter wavelengths. The stable configurations of electrons around an atom are literally standing waves, like the vibration of a guitar string or the ringing of a bell (more precisely, a spherical bell). The closest configuration with the simplest possible harmonic, just one “up and down” of the wave, is the “ground state”. An electron has very little mass, and so very little energy, and so the wavelength is very long (for a particle), and so the ground state is a long way from the nucleus.

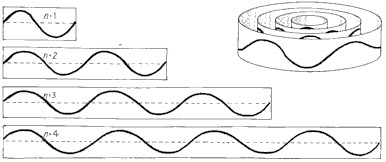
The possible standing waves of an electron determine the possible states it can occupy and how far it stays from the nucleus.

The “Bohr radius”, which is basically the distance between the nucleus and the electron in a hydrogen atom, is given by $r_e=\frac{4\pi\epsilon_0\hbar^2}{m_ee^2}$ . Swap out that electron mass, $m_e$ , for a 207-times-greater muon mass, $m_\mu$ , and suddenly that Bohr radius shrinks about 200-fold. I say “about” because the important quantity is the “reduced mass“, which is interesting if you know what the reduced mass is and distracting and unimportant if you don’t. So muonic hydrogen is physically much smaller than regular hydrogen, and therefore the positive nuclei stay shielded from each other until they’re much closer.

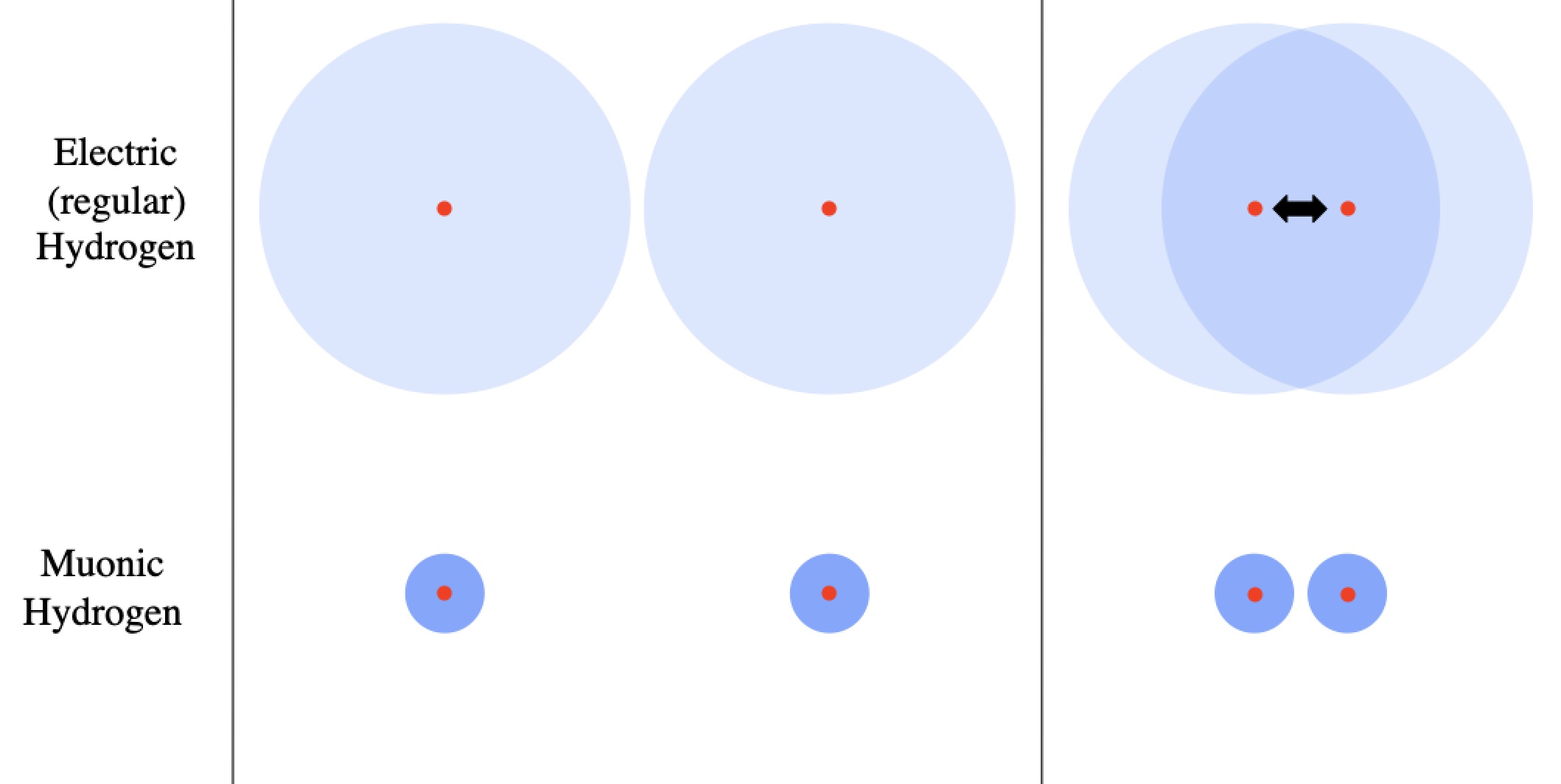
Outside of an atom there’s almost no net pull or push for any protons (or any other charged particle), but once you’re inside the electron shell no longer shields the charge of the nucleus. However, muonic hydrogen is smaller, meaning the repulsive force doesn’t kick in until the atoms are ~200 times closer, meaning it takes less energy to bring the atoms together.

It is so much easier to bring muonic hydrogen together, that it doesn’t even need to be hot to fuse. We can initiate an actual, honest-to-god fusion reaction at below room temperature, which is exactly what cold fusion is supposed to be. Even better, since muons live to such a ripe old age (millionths of a second is a long time compared to the amount of time it takes particles to do practically anything), they can be carried into one fusion reaction, bounce out, form muonic hydrogen with another proton, fuse again, and repeat the process a dozen or so times before finally decaying. So technically, cold fusion is not only possible, but has been done for the better part of a century. The problem is that it’s not useful.

Muons aren’t cheap. Like all fancy particles (“fancy” = “unstable”), to create muons you need enough energy to be released to spontaneously create new particles, some of which may be muons. Being naturally attractive and frugal, undergraduate physicists rely on high-energy cosmic ray interactions in the upper atmosphere to generate muons for their undergraduate projects and just wait for them to rain down into their labs. You’ve been hit by a couple hundred muons a minute for your entire life (more when you’re lying down, because more of you is exposed to the sky). But if you want lots of muons on demand, you need a particle cannon, and particle cannons (as you might imagine) require power. About twice as much power as you can recover from the muon-assisted cold fusion the particle cannon enables, even under ideal conditions.

Cold fusion: it works, but don’t bother.

We’ve had decades to study muon-catalyzed fusion, and so far there’s been very little progress. This may be a fundamental limit, not surpassable by any technology, ever. But, if you’re young, it may be worth your lifetime to find a way to prove that wrong. The beauty of fundamental research is that even if you fail, you’ll figure out some other unexpected stuff along the way.

Posted in -- By the Physicist, Particle Physics, Physics | 4 Comments

Q: How likely is it that there’s dark matter in me right now?

Posted on August 31, 2020 by The Physicist

Physicist: Probably very likely! Probably!

When we look out into the universe we find that on galactic scales and up that most of the mass in the universe is “dark”. Based on how galaxies form, move, collide, and bend light we can infer that the large majority of the matter creating gravity out there interacts with everything, including itself, only through gravity.

Like all the other matter, the Milky Way’s dark matter is zipping around at a fair clip. Our solar system (and all the stars close enough to see with the naked eye) are orbiting the galaxy at about 220 km per second. Around here we’re all orbiting in more or less the same way so, like cars on a highway, relative to each other we’re traveling much slower; a mere few dozen km per second. But dark matter doesn’t have to “stay in its lane”. Like cars driving across a highway, matter in a random orbit tends to find itself in an unfortunate situation sooner than later, so orbiting in formation is just something that normal matter does. Or rather what it does after a violent process of elimination (and that’s why Saturn’s rings, the solar system, and the entire galaxy are all roughly flat).

An unfortunate situation.

Not interacting means that dark matter orbits galaxies in puffy, roughly spherical “dark matter halos”; a cloud of randomly orbiting stuff that barely notices all of the stars it passes by/through. We can expect any individual bit of dark matter around us to be moving at on the order of hundreds of km per second.

All this to say, “having dark matter in your body” doesn’t mean you’ve come down with a bad case of WIMP-iness. You’re not slowly collecting dark matter in your thyroid. Even if you could detect dark matter (which has proven to be tricky) in your body, by the time you realized it was there it would already be long gone. Literally. The best human reaction times of any kind are around a tenth of a second, so any dark matter you find in your body is likely to be dozens of km away by the time you are physiologically able to know about it. Which is… useful knowledge?

We can see that dark matter is there and we can pontificate about what it’s like, but we’ve never once seen it do anything other than simply exist in extremely large quantities. We think it’s matter, because it produces gravity. From the way it arranges itself around galaxies, we don’t think it ever interacts, slows down, or changes direction except through gravity. We’re standing in an extremely thin, omni-directional rain of invisible, intactile stuff that passes through us at stupefying speeds, and that’s about all we can say about the dark matter around us it. Unfortunately, for this question, we have no idea how much mass particles of dark matter have, or even if dark matter takes the form of particles at all (although, if it didn’t, quantum mechanics would have a lot of explaining to do).

So here’s a wild estimate. The radius of our galaxy is about 129,000 light years and the total amount of dark matter is in the neighborhood of 10¹² solar masses, or about 2×10⁴² kg of mass. Assuming that’s evenly and spherically distributed around the galaxy (which is a rough, but not terrible, estimate), that’s a density of about 2.6x10^-22 kg/m³. So if you gathered up all of the dark matter in the Earth (or an empty Earth-sized volume, for all that dark matter cares) you’d have a bit less than 1 kg.

If each dark matter particle was as massive as a bowling ball (which… maybe?), then there’s no dark matter in you right now. At any moment there’d be one place within a few Earth radii that had any dark matter, and that wouldn’t happen to be where you are. There just isn’t enough luck. But for the same reason that it’s easier to dodge water balloons than rain, you’re more likely to have dark matter in you if it’s made up of more particles with less mass each.

We can measure how dense dark matter is on galactic scales, but we have no idea how big a single particle of dark matter is. Bigger particles are less likely to be inside of you (or any other particular place) and smaller particles with the same total mass are more likely to be everywhere.

The average adult (human) mass is 62 kg, which implies a volume of 0.062 m³ because, conveniently, people have the same density as water (which is why you can comfortably swim under water) and water is exactly one metric ton per cubic meter (which is not a coincidence). So given that rough dark matter density and that average person-volume, your share is about 1.6x10^-23 kg. That doesn’t sound like a lot, because it isn’t. A single red blood cell is more than a billion times bigger (about 2.7x10^-14 kg). But particles are really small. The most massive verified particle is the Higgs boson, which weighs in at a hefty 2.2x10^-25 kg. If dark matter particles are equally as massive, then you should have about 7oish of them in your body at all times; zipping through you at colossal speeds. At the other end of the scale are neutrinos, with a mass of no more than 2.14x10^-37 kg. If dark matter particles are neutrino-sized, then you presently overlap with at least 75 trillion of them.

So if dark matter is made of particles that are not-a-hell-of-a-lot-bigger than every other known particle, then if you took a snapshot of yourself right now, the chance that you have dark matter in your body is as close to 100% as you’d care to imagine. That drops suddenly as the masses of those particles gets close to around 10-100 times more massive than the most massive known particle (being more specific is a little silly considering how rough the density estimate is).

But don’t get too excited. The ten or so yoctograms of extra matter in your body is a long way from producing enough gravity to ruin your day, and gravity is the only tool dark matter has to work with. “There’s dark matter in me right now!” is a great conversation starter and ender, but that’s about the extent of its personal relevance.

The colliding planets picture is from here.

Posted in -- By the Physicist, Astronomy, Paranoia, Particle Physics, Physics, Probability | 8 Comments

Q: How big is the universe? What happens at the “edge”?

Posted on June 30, 2020 by The Physicist

Physicist: Quite.

This is a surprisingly subtle question. The problem is, we can’t see the entire universe. Imagine standing in a vast prairie or floating on a ship at sea. Looking around you see a lot of the same stuff, about the same everywhere, and extending to the edge of your vision.

There’s a limit to what we can see. The “edge” of the visible universe is a “horizon”. There’s probably a lot more of the universe beyond that horizon, but it officially doesn’t matter.

The “edge” at the limit of your vision is the horizon. Something moving away from you is visible until it gets to the horizon and then it disappears (starting at the bottom). On Earth, the effects of the horizon come from the ground physically blocking your view. Spacetime horizons are a bit different, but they share one important commonality with our Earthly horizon; if you go to where the horizon is, you don’t notice anything special.

The spacetime horizon you’re most likely familiar with is the “event horizon” of a black hole, forming the “surface”. The event horizon is the limit beyond which nothing can escape (including light, which is how black holes earn their name). Something above the horizon is visible and, perhaps with great effort, can escape to meet an outside observer. Anything below the event horizon is gone forever.

The event horizon is not just a boundary in space, it is in some sense a boundary in time. Someone falling into a black hole shouldn’t notice anything too exciting at the event horizon. Extreme gravity and the terrifying knowledge that your falling into a black hole notwithstanding, passing through the event horizon shouldn’t be something that really stands out to you.

The lower something is in a gravity well, the less it experiences time. We can directly measure the effect due to Earth’s gravity (at microseconds per mile up per year, it’s usually not worth worrying about). At the event horizon of a black hole this slowing effect reaches it’s natural extreme, and time stops. If you watch something falling into a black hole, it appears to move slower and slower as it approaches the horizon, until its last moment, just before passing through the horizon, are stretched out infinitely. Things only emit so much light in a given moment and forever is a long time (so far), so things falling in appear very slow and very dim. You won’t see things actually get to the horizon and stop, you’ll see them get close and then fade quickly from view. There is some moment that never quite comes and the time until that moment stretches out forever.

Light released just prior to the moment of passing through the horizon will eventually escape to an observer. Light release just after will not. The cosmological event horizon is remarkably similar. It’s presently about 16 billion light years away, in every direction.

The cosmological horizon is caused by the expansion of the universe. You can picture this as being like ants crawling on a balloon. As the balloon expands only ants that are close to each other will be able to run into each other; more distant ants can crawl at each other at full speed, but the expansion will add more rubber between them than their movement subtracts. If something moving away from us passes through the horizon, then the last light it emits before crossing the horizon will take forever to get to us.

The universe hasn’t existed forever and a lot of stuff has happened in its history, so the oldest light we can see doesn’t come from close to the cosmic event horizon. Even so, the same slowing/reddening effect is visible to the naked eye.

A lot of galaxies in a very small corner of the sky. Most of the color difference comes from “cosmological redshift”; the redder a galaxy is, the farther away it is.

The first galaxies date to when the universe was a bit under an billion years old, with a redshift of a bit under ten, meaning that light coming from them is ten times as stretched out and the galaxies appear to be experiencing time at a tenth the usual rate. The oldest light we can see is the cosmic microwave background, which has been traveling for 13 billion years and redshifted by a factor of 1100. We can’t see any farther with light; the CMB is like the blue of the sky, completely overwhelming the sky behind it.

So if you were standing 16 billion light years away, at the present location of the cosmological event horizon (from Earth’s perspective), you wouldn’t see anything too surprising. The universe looks more or less the same everywhere. You could send a signal to Earth, but you’d be in the most frustrating possible place to do it: just close enough that the signal will make it, but just far enough that it will take literally forever. If anyone on Earth ever saw you (in the extreme future), you’d appear frozen in time and invisibly dim.

In the mean time, the expansion of the universe doesn’t just cause the horizon to exist, it constantly forces things to fall beyond it. We won’t ever directly see things fall beyond the horizon for the same frustrating reason we won’t see things quite fall into black holes. Like things approaching the event horizon of a black hole, extremely distant things get redder, and slower, and fade from view while never quite reaching some prescribed moment.

So there’s no real “edge” to the universe. Just like the horizon on Earth, the cosmic event horizon is a regular place. Being like everywhere else, there’s nothing to notice. Nothing really happens when you cross it. Technically, some astronomy nerd sixteen billion light years away can point out that once you cross each others horizons, you no longer have the option to send each other messages.

The “out in a field” picture is from here.

Posted in Uncategorized | 17 Comments

Q: What if the particles in the double slit experiment were conscious? Could you ask them which slit they went through afterwards?

Posted on May 30, 2020 by The Physicist

The original question was: I find the double slit experiment super interesting and have lots of questions about it. But here’s one.

What if the particles you send through the slits are conscious? You send them through without measuring anything, and see an interference pattern. Afterwards, can you ask them which slit they went through?

More generally, maybe someone far far away can somehow infer that I am in a superposition, eating chocolate and/or vanilla ice cream. Later on, could they come down here and tell me about it? And ask which one I thought I was eating?

Physicist: This is a beautiful question.

In the early 1800s Young first did his double slit experiment, showing that light is a wave; a fact that’s more interesting than mind blowing. That was fine until the early 1900s, when a compounding of theoretical issues and empirical evidence revealed that light is also particle, in that it only seems to interact in discrete “quantized” chunks; a combination of facts more confusing than mind blowing.

An extremely good question, upon learning that light behaves like a particle, is to repeat the double slit experiment, but keep the light intensity so low that only a single photon is present at a time. If the universe were sympathetic to the human plight or placed any value on the peaceful sleep of physicists, then the result of this experiment would be a transformation of the interference fringes into a pair of bumps, one for each slit, as the photons run out of other photons to interfere with.

Coherent light passing through a pair (or more) of slits generates patterns as the waves of light from the two slits “interfere” with each other. The exact same pattern persists even when only a single photon is allowed through at a time (although it takes longer for the pattern to be clearly visible, since it’s built up one dot at a time).

When we actually do this experiment, we find that the same pattern continues to show up. Evidently, each individual photon interferes with itself, as though it had gone though both slits; a realization that’s more mind blowing than anything else.

It’s this “superposition” property of photons that makes them fundamentally quantum and it’s responsible for interference. An individual photon can pass through both slits and, although we can’t witness both versions of the photon, we can infer that they both existed through the interference pattern their combination forms.

It turns out that if there’s any way whatsoever to figure out which slit the photon went through, even if you don’t bother to find out, then there is no interference pattern. If you know that the photon went through the left slit (and genuinely doesn’t matter how you know), then the pattern it follows impacting the screen will contain no contribution from the right slit.

For example, if you put perpendicular polarizers in front of the slits, then you can “mark” photons. If the left slit is vertically polarized and the right is horizontal, then there’s no interference between the slits; we see two bumps, each made up of light from a particular slit with a particular polarization. You don’t actually have to check the polarization of any photon; the fact that it’s possible to know for sure which slit the photon came from (by measuring it with a polarizer) means that the two paths are “distinguishable”.

If both slits have vertical polarizers, then all of the light is vertically polarized and there’s no way to tell which slit the photon came from. Since the polarization of the photons is independent of which slit they went through, we see interference fringes again: many bright spots, two slits. Notice that this means that the polarizers themselves don’t “damage” the state of the photons passong through. The interference patterns really are dependent on the distinguishability of the slits.

So this may actually answer the question. We can ask each photon which slit they just came from by measuring their polarization. When the polarization state of the photons is used to “mark” them, they “remember” which slit they went through and there is no interference pattern. When they “don’t remember”, then there is an interference pattern. The photon’s polarization is being used here as a “pointer state”, and it’s a good way to talk about “memory”.

The term “pointer state” refers to a physical system that physical records a measurement result. For example: the position of a thing that points.

This physical record is sometimes called a “pointer state”, referring to the actual, physical state of a pointer pointing at something.

Through out the 20th century we found that photons aren’t special. Electrons, entire atoms, molecules with thousands of atoms, everything that has ever been directly tested has demonstrated interference effects as well as particle-like behavior, just like light. In fact, with coherence times measured in minutes and entanglement established between continents, one begins to suspect that quantum mechanics may be the general rule. What if everything, including us, is a quantum system? What does it feel like to be in a superposition of eating chocolate and/or vanilla ice cream states?

In the “Wigner’s Friend” thought experiment, the Friend is asked to do some kind of quantum measurement, like opening Schrödinger’s Cat’s box, and then report the results to Wigner a little later. The question is, does Wigner’s Friend’s observation of the Cat “collapse” its state, or do the Friend and Cat end up in a superposition of states together, alive/relieved and dead/horrified?

Remarkably, we may be able to answer that question experimentally without mentioning consciousness more than just this once. We can talk about pointer states under the rather broad umbrella of “something that keeps a physical record of the result of a quantum measurement”, which includes conscious minds, trained dogs, chalkboards, particular arrangements of rocks, etc. A conscious human mind is remarkable. Fine. But all we need here is “a brain includes a physical record of events”. We can still feel superior, but for our purposes, the polarization state of a photon, a single qubit of information, is sufficient.

Brains are arguably better that chalkboards. But even though brains can think and love and consider qualia and generally be conscious, the only thing that minds do that’s important for pointer states is remembering stuff. Chalkboards can be used to “physically encode the result of a quantum measurement” just as well as a brain (or a rock), so they’re both good enough.

In “Experimental rejection of observer-independence in the quantum world” Wigner’s Friend is a clever device that measures and records the horizontal/vertical polarization of one photon onto another, using a combination of entangled photons, half and quarter wave plates, polarizing beam splitters, and single photon detectors (it was not easy). This Friend is sealed inside an “information proof” Lab, like the box containing Schrödinger’s Cat. The only record of the first photon’s state is the second photon, not some “Wigner’s Clipboard” left in the lab. Finally, Wigner’s Friend can alert the outside world that a measurement has been successfully done, without reporting the result.

a, an incoming photon in and unknown state, enters Wigner’s Lab. Wigner’s Friend measures the horizontal/vertical polarization of a by firing off two photons with the same polarization, b and c. The polarizing beam splitter always reflects horizontal light and always passes vertical. If a and b have the same polarization, then one photon will exit each branch of the beam splitter, either both vertical (and passing straight through) or both horizontal (and both reflected). In that case, a and c have the same polarization, a in its original state and c in the same state; photon c carries a physical record of the state of a. b is used to announce a successful measurement (a success is only counted when all three photons are detected, in their expected place). So a detection-and-record isn’t usually successful, but we can tell when it works.

This is a bit of a digression, so if you’re interested, you can read a more detailed digression into this experiment here or read the original paper here. Suffice it to say:

-Photon A goes into the Lab and gets measured in the horizontal/vertical direction, but is left undisturbed. Whether horizontal or vertical, $|\rightarrow\rangle$ or $|\uparrow\rangle$ , the state of A is verifiably the same before and after passing through the Lab.

-Photons A and C emerge from the Lab, where the polarization of C is a copy of the result of a vertical/horizontal meansurement on A. We can verify the output (say,two vertical states) given the input (say, one vertical state) easily.

-No other record of the state is kept. This experiment is shockingly clean: a verifiably accurate measurement of a photon is done, the one and only record of that result is written onto another single photon, and the two are sent on their way.

The question is, what happens to Wigner’s Friend, when he’s given a diagonally polarized photon

$|\nearrow\rangle = \frac{|\uparrow\rangle + |\rightarrow\rangle}{\sqrt{2}}$

which is a equal superposition of vertical and horizontal polarization states? Remarkably, Wigner’s Friend (the second photon) enters a superposition of states as well.

$|\nearrow\rangle_a = \frac{|\uparrow\rangle_a + |\rightarrow\rangle_a}{\sqrt{2}}\quad\longrightarrow\quad\frac{|\uparrow\rangle_a|\uparrow\rangle_c + |\rightarrow\rangle_a|\rightarrow\rangle_c}{\sqrt{2}}$

This is a Bell state! It means that the original photon and the result of a measurement on it are entangled with each other. Bell states are demonstrably non-classical, very quantum mechanical, phenomena. Being in this Bell state means that, even though A and C are in a superposition of states, if one is later found to be, say, horizontal, then so will the other. Regardless of the result, Wigner’s Friend still did the measurment accurately and only saw the one result.

The original photon is still in a superposition of states, and so is the result of the measurement on it. It’s fairly simple to measure pairs of photons in the “Bell basis“, allowing us to tell the difference between $|\nearrow\rangle_a$ and

$|\nwarrow\rangle_a = \frac{|\uparrow\rangle_a - |\rightarrow\rangle_a}{\sqrt{2}}\quad\longrightarrow\quad\frac{|\uparrow\rangle_a|\uparrow\rangle_c - |\rightarrow\rangle_a|\rightarrow\rangle_c}{\sqrt{2}}$

which is the other diagonally polarized state.

Evidently, measurment doesn’t collapse states, it entangles them. The result of a measurement is not an objective thing! It can be in a superposition of states just like everything else. Assuming quantum laws are universal (they seem to be) and assuming we, our memories, are pointer states (it’s hard not to be), and assuming that it’s possible to “information isolate” people from each other (in the extreme, zero-information sense of the physical experiment), then we can describe what it would be like to be Wigner’s Friend.

Taking the photon experiment as guide, we’ll consider a perfectly-isolated Lab that includes an ice cream machine that dispenses either vanilla or chocolate depending on the result of a polarization measurement of a single incoming photon. We can feel confident that if we feed in a $|\nearrow\rangle = \frac{|\uparrow\rangle + |\rightarrow\rangle}{\sqrt{2}}$ photon, then Wigner’s Friend will eat a superposition of flavors $\frac{|\uparrow\rangle|vanilla\rangle + |\rightarrow\rangle|chocolate\rangle}{\sqrt{2}}$ . However, if you asked Wigner’s Friend what he experienced, he’d tell you an answer; either vanilla or chocolate, but not both. He doesn’t experience the superposition as anything strange.

In the last few years we’ve managed to establish entanglement between continents using intermediating satellites. With a huge effort, we could set up something like that between Earth and Mars. Here on Earth the result of measurements on these entangled pairs would be used for ice cream choices and on Mars, sheilded by the fact that information can’t travel faster than light, uses their entangled pairs to infer that people on Earth (the ice cream eater, at least) are in superpositions. This isn’t a useful trick. When you actually ask “what flavor did you get?”, you’ll get a direct, non-quantum answer. But technically, you could be confident that someone on the far end of your entangled pair is eating a superposition of flavors. Until you can talk to them. Even if you don’t.

Posted in -- By the Physicist, Paranoia, Philosophical, Physics, Quantum Theory | 17 Comments

A Quantum Computation Course 4: Full Measure

Posted on April 29, 2020 by The Physicist

Physicist: If you’ve made it through the last fifteen lectures, you’ll enjoy the last installment. It’s about using entanglement as a tool to measure, communicate, control, and ultimately blow our own minds.

Using entanglement to teleport entanglement; the secret sauce of a quantum network.

Lecture 16: Quantum Measurements

Lecture 17: Quantum Noise

Lecture 18: Error Correction

Lecture 19: Quantum Networks

Lecture 20: Hard Limits

Lecture 21: The Quantum Eraser

Lecture 22: The Observer

Posted in Uncategorized | 5 Comments

A Quantum Computation Course 3: Rise of the Quanta

Posted on March 30, 2020 by The Physicist

Physicist: The last five chapters should have left you terrified. These should leave you inspired. With all of the mathematical tools established, these lectures get into some of the remarkable things that quantum hardware can do.