Q: If the number of ancestors you have doubles with each generation going back, you quickly get to a number bigger than the population of Earth. Does that mean we’re all a little inbred?

Posted on April 25, 2014 by The Physicist

Physicist: In a word: yes.  But it’s not a problem in large populations.

The original questioner pointed out that in the age of Charlemagne (more or less when everybody’s 40-greats grandfolk were living) the world population was between 200 and 300 million, and yet 2^40 (the number of ancestors you would have with no overlap) is 1,099,511,627,776.  As it happens, 1.09 trillion is bigger than 300 million (math!).  That means that your average ancestor alive 1200 years ago shows up in your 40-generation-tall family tree at least around 4,000 times.  That redundancy is likely to be much higher.  Many of the people alive during the reign of Chuck the Great left no descendents, and while your family tree is probably wider than you might suspect, most of your ancestors probably came from only a few regions of the world.  Most people will start seeing redundancy in their family tree within a dozen generations (small towns and all that).  Fortunately, “redundancy” isn’t an issue as long as the genetic pool is large enough.

The biology of living things assumes that things will break and/or mess up frequently.  One of the stop-gaps to keep mistakes in the genetic code from being serious is to keep two different copies around.  This squares the chance of error (which is good).  If one strand of DNA gets things right 90% of the time, then if you have access to two strands that gets bumped up to 99% (of the 10% the first missed, the second picks up 90%).  However, if you have two identical copies, then this advantage goes away because both copies of the DNA will contain the same mistakes.  That’s a why (for example) red/green colorblindness is far more common in dudes (who have 1 X chromosome) than in ladies (who have two).  Don’t get too excited ladies; gentlemen still have two copies of all of the other chromosomes.  Also, that 90% thing is just for ease of math; if 1 in 10 genes were errors, then life wouldn’t work.

The two copies that each of us carry around are only combined together in the germline (found in our junk), and that combination is what’s passed on.  What makes the cut into the next generation is pretty random, which helps ensure genetic diversity (and is why siblings look similar, while identical twins look the same).

As long as genes have a chance to mix around, the chance of an error showing up in the same person twice is pretty low.  That said, there are a lot of things that can go “wrong” so, statistically speaking, everybody‘s got at least a few switches flipped backwards.  It happens.  If it weren’t for mistakes, biology would be pretty boring.

An impressive, but somewhat speculative computer model, says it’s likely that we all have a common ancestor (a long-dead someone who is directly related to everyone presently living) a mere few thousand years ago.  That person is very unlikely to be unique, and their genes are so watered down by now that it barely matters who/where they were.  What the computer model is saying is that, given what we know about human migration and travel, a “single drop in the human genetic pool” only takes a few thousand years to diffuse to the farthest corners of the world.

So we all have some repeated ancestry, but it’s no big deal.  You still have lots of ancestors with lots of genetic diversity.

Posted in -- By the Physicist, Biology, Evolution, Probability | 12 Comments

Q: Why are many galaxies, our solar system, and Saturn’s rings all flat?

Posted on April 18, 2014 by The Physicist

Physicist: This may be the shortest answer yet: “accretion“.

Stuff out there gets flat.

Accretion: making stuff flat for billions of years.

Accretion is the process of matter gravitationally collapsing from a cloud of dust or gas or (usually) both.  Before thinking about what a big cloud of gas does when it runs into itself, it’s worth thinking about what happens to just two clumps of dust when they run into each other.

In a perfectly elastic collision dust will bounce out at about the same angle that it originated. Most collisions are inelastic, which means they lose energy and that the angle between the dust particle's trajectories decreases in a collision. In the most extreme case.

Most collisions are inelastic, which means they lose energy and that the particles’ trajectories are “averaged” a little.  In the most extreme case things will stick together.

In a perfectly elastic collision objects will bounce out at about the same angle that they came in.  Most collisions are inelastic, which means they lose energy and the angle between the objects’ trajectories decreases after a collision.  In the most extreme inelastic case the particles will stick together.  For tiny particles this is more common than you might think.

Normal salt, in zero gravity, clumping together spontaneously due to electrostatic forces.

Table salt, in zero gravity, spontaneously clumping due to electrostatic forces (click image for movie).

Over time collisions release energy (as heat and light).  This loss of energy causes the cloud to physically contract, since losing energy means the bits of dust and gas are moving slower (and that means falling into lower and lower orbits).  But collisions also make things “average” their trajectories.  So while a big puffy cloud may have bits of dust and gas traveling every-which-way, during accretion they eventually settle into the same, average, rotational plane.

Each atom of gas and mote of dust moves along its own orbital loop, pulled by the collaborative gravitational influence of every other atom and mote (there’s no one point where the gravity originates).  While the path of each of these is pretty random, there’s always net rotation in some direction.  The idea is any cloud in space starts out with at least a little bit of spin.  This isn’t a big claim; pour coffee into a cup, and at least some little bits will be turning.  That same turbulence shows up naturally at all larger-than-coffee-cup scales in the universe (although typically not much smaller).  So, on average, any cloud will be turning in some direction.

Things in the cloud will continue to run into each other until every part of it has done one of three things: 1) escaped, 2) fallen into the center, or 3) moves with the flow. Most of the cloud ends up in the center.  For example, our Sun makes up 99.86% of the matter in the solar system.  The stuff that stops colliding and goes with the flow forms the ring.  Anything not in the plane of the ring must be on an orbit that passes through it, which means that it will continue hitting things and losing energy.  Eventually, the “incorrectly orbiting” object will either find itself co-orbiting with everything else in the ring, or will loose enough kinetic energy to fall into the planet or star below.  By the way, there’s still a lot of “unaffiliated” junk in our solar system that’s still waiting to “join” a planet.

Those rings are pretty exciting places themselves.  Inside of them there are bound to be “lumps” of higher density that draw in surrounding material.  Eventually this turns into smaller accretion disks within the larger disk.  Our solar system formed as a disk with all of the planets forming within that disk in the “plane of the ecliptic”.  One of those lumps became Jupiter, which has its own set of moons that also formed in an accretion disk around Jupiter.  In fact, Jupiter’s moons are laid out so much like the rest of the solar system (all orbiting in the same plane) that they helped early astronomers to first understand the entire solar system.  It’s hard to see how the planets are moving from a vantage on the surface of one of those moving planets (Earth), so it’s nice to have a simple boxed example like Jupiter.

The planets always lie within the same plane. Since the Earth is also in this plane, the ecliptic is a band in the sky

The planets always lie within the same plane, “the ecliptic”.  Since the Earth is also in this plane, the ecliptic appears as a band in the sky where the Sun and all of the planets can be found.  Similarly, Jupiter’s moons also lie in a plane.

That all said, those lumps add an element of chaos to the story.  Planets and moons don’t simply orbit the Sun, they also interact with each other.  Sometimes this leads to awesome stuff like planets impacting each other and big explosions.  One of the leading theories behind the formation of our Moon is one such impact.  But these interactions can sometime slingshot smaller objects into weird, off-plane orbits.  Knowing that planets tend to be found in the same plane make astronomer’s jobs that much easier.  From Earth, the ecliptic appears as a thin band that none of the other planets stray from.  Pluto was the second dwarf planet found (after Ceres) because it orbits close to the plane of all the other planets, and is inside this band.  The dwarf planet Xena and its moon Gabriel orbit way off of the ecliptic, which is a big part of why they weren’t found until 2005 (the sky is a big place after all).  Xena and Gabriel’s official names are “Eris” and “Dysnomia” respectively, but I support the original discoverer’s labels, because they’re amazing.  So things can have wonky orbits, but they need to do it way the crap out there where they don’t inevitably run into something else.  Xena is usually about twice as far out as Pluto, which itself is definitively way the crap out there.

Not all matter forms accretion disks.  In order for a disk to form the matter involved has to interact.  Gas and dust does a great job of that.  But once they’ve formed, stars barely interact at all.  For example, when (not if!) the Andromeda and Milky Way galaxies hit each other, it’s really unlikely that any stars will smack into each other (they’re just too small and far apart).  However, the giant gas clouds in each should slam into each other and spark a flurry of new star formation.  In four billion years the sky will be especially pretty.

Posted in -- By the Physicist, Astronomy, Physics | 17 Comments

Q: How do you define the derivatives of the Heaviside, Sign, Absolute Value, and Delta functions? How do they relate to one another?

Posted on April 12, 2014 by The Physicist

Physicist: These are four standard reference functions.  In the same way that there are named mathematical constants, like π or e, there are named mathematical functions.  These are among the more famous (after the spotlight hogging trig functions).

The Sign, Delta, Absolute Value, and Heaviside functions.

The Sign, Delta, Absolute Value, and Heaviside functions.  The graphs on top are the slope of the graphs on the bottom (and slope=derivative).

The absolute value function flips the sign of negative numbers, and leaves positive numbers alone.  The sign function is 1 for positive numbers and -1 for negative numbers.  The Heaviside function is very similar; 1 for positive numbers and 0 for negative numbers.  By the way, the Heaviside function, rather than being named after its shape, is named after Oliver Heaviside, who was awesome.

The delta function is a whole other thing.  The delta function is zero everywhere other than at x=0 and at x=0 it’s infinite but there’s “one unit of area” under that spike.  Technically the delta function isn’t a function because it can’t be defined at zero.  The “Dirac delta function” is used a lot in physics (Dirac was a physicist) to do things like describe the location of the charge of single particles.  An electron has one unit of charge, but it’s smaller than basically anything, so describing it as a unit of charge located in exactly one point usually works fine (and if it doesn’t, don’t use a delta function).  This turns out to be a lot easier than modeling a particle as… just about anything else.

The derivative of a function is the slope of that function.  So, the derivative of |x| is 1 for positive numbers (45° up), and -1 for negative numbers (45° down).  But that’s the sign function!  Notice that at x=0, |x| has a kink and the slope can’t be defined (hence the open circles in the graph of sgn(x)).

The derivative of the Heaviside function is clearly zero for x≠0 (it’s completely level), but weird stuff happens at x=0.  There, if you were to insist that somehow the slope exists, you would find that no finite number does the job (vertical lines are “infinitely steep”).  But that sounds a bit like the delta function; zero everywhere, except for an infinite spike at x=0.

It is possible (even useful!) to define the delta function as δ(x) = H'(x).  Using that, you find that sgn'(x) = 2δ(x), simply because the jump is twice the size.  However, how you define derivatives for discontinuous functions is a whole thing, so that’ll be left in the answer gravy.

Answer Gravy: The Dirac delta function really got under the skin of a lot of mathematicians.  Many of them flatly refuse to even call it a “function” (since technically it doesn’t meet all the requirements).  Math folk are a skittish bunch, and when a bunch of handsome/beautiful pioneers (physicists) are using a function that isn’t definable, mathematicians can’t help but be helpful.  When they bother, physicists usually define the delta function as the limit of a series of progressively thinner and taller functions (usually Gaussians).

One of the simplest ways to construct the delta function is the series of functions shown here (and infinitely many more).

One of the simplest ways to construct the delta function is the series of functions fn(x) = n, 0 ≤ x ≤ 1/n (the first four of which are shown).  The area under each of these is 1, and most/many of the important properties of delta functions can be derived by looking at the limit as n→∞.

Mathematicians take a different tack.  For those brave cognoscenti, the delta function isn’t a function at all; instead it’s a “distribution”, which is a member of the dual of function space, and it’s used to define a “bounded linear functional”.

So that’s one issue cleared up.

A “functional” takes an entire function as input, and spits out a single number as output.  When you require that the functional is linear (and why not?), you’ll find that the only real option is for the functional to take the form F(g) = \int f(x)g(x)\,dx.  This is because of the natural linearity of the integral:

\begin{array}{ll}F(g + h) \\= \int f(x)\left(g(x)+h(x)\right)\,dx \\= \int f(x)g(x)\,dx + \int f(x)h(x)\,dx \\= F(g) + F(h)\end{array}

In F(g) = \int f(x)g(x)\,dx, F is the functional, f(x) is the distribution corresponding to that functional, and g(x) is the function being acted upon.  The delta function is the distribution corresponding to the functional which simply returns the value at zero.  That is, \int \delta(x)g(x)\,dx = g(0).  So finally, what in the crap does “returning the value at zero” have to do with the derivative of the Heaviside function?  As it happens: buckets!

Assume here that A<0<B,

\begin{array}{ll} \int_A^B \delta(x)g(x)\,dx \\[2mm] = H(x)g(x)\big|_A^B - \int_A^B H(x)g^\prime(x)\,dx & \textrm{(integration by parts)} \\[2mm] = H(B)g(B) - H(A)g(A) - \int_A^B H(x)g^\prime(x)\,dx \\[2mm] = H(B)g(B) - \int_0^B H(x)g^\prime(x)\,dx & (H(x)=0, x<0) \\[2mm] = g(B) - \int_0^B g^\prime(x)\,dx & (H(x)=1, x>0) \\[2mm] = g(B) - g(x)\big|_0^B & \textrm{(fundamental theorem of calculus)} \\[2mm] = g(B) - \left[g(B) - g(0) \right] \\[2mm] =g(0) \end{array}

Running through the same process again, you’ll find that this is a halfway decent way of going a step further and defining the derivative of the delta function, δ'(x).

\begin{array}{ll} \int_A^B \delta^\prime(x)g(x)\,dx \\[2mm] = \delta(x)g(x)\big|_A^B - \int_A^B \delta(x)g^\prime(x)\,dx \\[2mm] = - \int_A^B \delta(x)g^\prime(x)\,dx \\[2mm] = -g^\prime(0) \end{array}

δ'(x) also isn’t a function, but is instead another profoundly abstract distribution.  And yes: this can be done ad nauseam (or at least ad queasyam) to create distributions that grab higher and higher derivatives of input functions.

Posted in -- By the Physicist, Equations, Math | 10 Comments

Q: What does “E=mc2” mean?

Posted on April 7, 2014 by The Physicist

Physicist: This famous equation is a little more subtle than it appears.  It does provide a relationship between energy and matter, but importantly it does not say that they’re equivalent.

First, it’s worth considering what energy actually is.  Rather than being an actual “thing” in the universe, energy is best thought of as an abstract (there’s no such thing as pure energy).  Energy takes a heck of a lot of forms: kinetic, chemical, electrical, heat, mechanical, light, sound, nuclear, etc.  Each different form has it’s own equation(s).  For example, the energy stored in a (not overly) stretched or compressed spring is 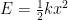E=\frac{1}{2}kx^2 and the energy of the heat in an object is 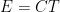E=CT.  Now, these equations are true insofar as they work (like all true equations in physics).  However, neither of them are saying what energy is.  Energy is a value that we can calculate by adding up the values for all of the various energy equations (for springs, or heat, or whatever).

The useful thing about energy, and the only reason anyone ever even bothered to name it, is that energy is conserved.  If you sum up all of the various kinds of energy one moment, then if you check back sometime later you’ll find that you’ll get the same sum.  The individual terms may get bigger and smaller, but the total stays the same.

For example, the equation used to describe the energy of a swinging the pendulum is 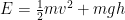E = \frac{1}{2}mv^2 + mgh where the variables are mass, velocity, gravitational acceleration, and height of the pendulum.  These two terms, the kinetic and gravitational-potential energies, are included because they change a lot (speed and height change throughout every swing) and because however much one changes, the other absorbs the difference and keeps E fixed.  There are more terms that can be included, like the heat of the pendulum or its chemical potential, but since those don’t change much and the whole point of energy is to be constant, those other terms can be ignored (as far as the swinging motion is concerned).

In fact, it isn’t obvious that all of these different forms of energy are related at all.  Joule had to do all kinds of goofy experiments to demonstrate that, for example, the sum of gravitational potential energy and thermal energy stays constant.  He had to build a machine that turned the energy of an elevated weight into heat, and then was careful to keep track of exactly how much of the first form of energy was lost and how much of the second was gained.

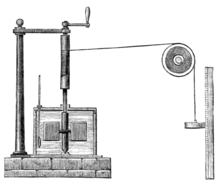
As the weight falls, it turns an agitator that heats the water. Joule's device couples the gravitational potential of the weight with the thermal energy of the water in a tank.

As the weight falls, it turns an agitator that heats the water. Joule’s device couples the gravitational potential of the weight with the thermal energy of the water in a tank.  The sum of the two stayed constant.

Enter Einstein.  He did a few fancy things in 1905, including figuring out a better way of doing mechanics.  Newtonian mechanics had some subtle inconsistencies that modern (1900 modern) science was just beginning to notice.  Special relativity helped fixed the heck out of that.  Among his other predictions, Einstein suggested (with some solid, consistent-with-experiment, reasoning) that the kinetic energy of a moving object should be 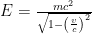E = \frac{mc^2}{\sqrt{1-\left(\frac{v}{c}\right)^2}}, where the variables here are mass, velocity, and the speed of light (c).  This equation has since been tested to hell and back and it works.  What’s bizarre about this new equation for kinetic energy is that even when the velocity is zero, the energy is still positive.

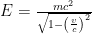Up to about 40% of light speed (mach 350,000), E = mc^2 + \frac{1}{2}mv^2 is a really good approximation of Einstein’s kinetic energy equation, E = \frac{mc^2}{\sqrt{1-\left(\frac{v}{c}\right)^2}}.  The approximation is good enough that ye natural philosophers of olde can be forgiven for not noticing the tiny error terms.  They can also be forgiven for not noticing the mc2 term.  Despite being huge compared to all of the other terms, mc2 never changed in those old experiments.  Like the chemical potential of the pendulum, the mc2 term wasn’t important for describing anything they were seeing.  It’s a little like being on a boat at sea; the tiny rises and falls of the surface are obvious, but the huge distance to the bottom is not.

So, that was Einstein’s contribution.  Before Einstein, the kinetic energy of a completely stationary rock and a missing rock was the same (zero).  After Einstein, the kinetic energy of a stationary rock and a missing rock were extremely different (by mc2 in fact).  What this means in terms of energy (which is just the sum of a bunch of different terms that always stays the same) is that “removing an object” now violates the conservation of energy.  E=mc2 is very non-specific and at the time it was written: not super helpful.  It merely implies that if matter were to disappear, you’d need a certain amount of some other kind of energy to take its place (wound springs, books higher on shelves, warmer tea, some other kind); and in order for new matter to appear, a prescribed amount of energy must also disappear.  Not in any profound way, but in a “when the pendulum swings up, it also slows down” sort of way.  Einstein also didn’t suggest any method for matter to appear or disappear (that came later).  So, energy is a sort of strict economy (total never changes) with many different currencies (types of energy).  Einstein showed that matter needed to be included in that “economy”, and that some things in physics are simpler if it is.

While it is true that the amount of mass in a nuclear weapon decreases during detonation, that’s also true of every explosive.  For that mater, it’s true of everything that releases energy in any form.  When you drain a battery it literally weighs a little less because of the loss of chemical energy.  The total difference for a good D-battery is about 0.015 picograms, which is tough to notice especially when the battery is ten billion times more massive.  About the only folks who regularly worry about the fact that energy and matter can be sometimes be exchanged are high-energy physicists.

Cloud chamber tracks like these provided some of the earliest evidence of particle creation, and have entertained aged nerds for decades.

Cloud chamber tracks like these provided some of the earliest evidence of particle creation and have entertained aged nerds for decades.

As far as a particle physicist is concerned, particles don’t have masses; they have equivalent energies.  If you happen to corner one at a party (it’s not hard, because they’re meek), ask them the mass of an electron.  They’ll probably say “0.5 mega-electronvolts” which is a unit of energy (the kinetic energy of a single unit of charge accelerated by 500,000 volts).  In particle physics, the amount of energy released/sequestered when a particle is annihilated/created is typically more important that the amount that a particle physically weighs (I mean, how hard is it to pick up a particle?).  So when particle physicists talk shop, they use energy rather than matter.  For those of us unbothered by creation and annihilation, the fact that rest-mass is a term included among many different energy terms is pretty unimportant.  Nothing we do or experience day-to-day is affected by the fact that rest-mass has energy.  Sure the energy is there, but changing it, getting access to it, or doing anything useful with it is difficult.

The cloud chamber picture is from here, and there’s a video of one in action here.

Posted in -- By the Physicist, Equations, Philosophical, Physics, Relativity | 25 Comments

Q: Is it possible to have a completely original thought?

Posted on April 1, 2014 by The Physicist

Physicist: Nope!  At least, not for the last 27 years.

The last truly, verifiably original thought was had by Kjersti Skramstad of Oslo, in October of 1987.  She reported her insight immediately, as all original thinkers do, and since then there’s been nothing new under the Sun.  That stunning insight, by the way, was “curling ville være lettere med lettere steiner!“.

In 1995 there was a lot of buzz around the scientists at Bell labs; they briefly skirted originality before it was realized that their entire venture had been sketched out, beginning-to-end, by Claude Shannon in one of his notebooks almost 50 years earlier.  In fact, there has been a quiet but insistent push in some industries to remove the phrase “reinventing the wheel” from common parlance, under the assertion that it is now redundant and applies to all invention.

In scientific circles the concern is fairly minimal.  There are enough “loose pieces” around that scientists will still be making great strides for decades.  For example, by combining lots of boring animals to create awesome crimes against nature (hippogriffs, cockatrices, manticores, etc.).  Or by taking an ordinary thing (e.g., elevators) and adding the word “space” to them (e.g., space elevators).  The ideas may be unoriginal, but science still happens when you try them out for the first time.

Piano -> Space piano

Piano -> Space Piano.  Science marches on.

For we ordinary folk, original thoughts aren’t too important, but artists (for whom originality pays the bills) have been in a panic since the late 70’s when it first became clear that the well of new ideas was running dry.  In particular, 1978 saw the album “More Songs about Buildings and Food” produced, bringing the epoch of original composition to an unceremonious close.  There’s some hope that Laurie Anderson may have done something completely novel with her masterpiece “three minutes and forty-four seconds of white-noise while wearing an extraneous prosthesis” but some more pessimistic parties have already drawn parallels to John Cage’s 4’33”.  Time will tell.

Oddly enough, no politicians have noticed.  Like, at all.

Posted in -- By the Physicist, April Fools | 34 Comments

Q: How can the universe expand faster than the speed of light?

Posted on March 5, 2014 by The Physicist

Physicist: You’ll often hear that “the universe is expanding faster than the speed of light”.  However, this statement is akin to statements like “green is bigger than happy”.  It’s not even wrong.

There are two big things to remember about the expansion of the universe.  First, the universe doesn’t expand at a particular speed, it expands at a speed per distance.  Right now it’s about 70 kilometers per second per megaparsec.  That means that galaxies that are about 1 megaparsec (1 parsec = 3 lightyears and change) away are presently getting farther away at the rate of 70 km every second, on average.  Galaxies that are 2 megaparsecs away are presently getting father away at the rate of 140 km every second, on average.

Notice the awkward phrasing there: distant galaxies are “getting farther away”, but oddly enough they are not “moving away”.

Initially, the distance between Red and Yellow is 1, and the distance between Red and Green is 2. After double the size of the "universe" the distances are 2 and 4, respectively. Yellow receded by 1, but Green receded by 2. Green would seem to be moving faster than Yellow, but in fact all of the dots are sitting still while the space they inhabit expands.

Initially, the distance between Red and Yellow is 1, and the distance between Red and Green is 2. After doubling the size of the “universe” the distances are 2 and 4, respectively. Yellow receded by 1, but Green receded by 2. Green would seem to be “moving” faster than Yellow, but in fact all of the dots are sitting still while the space they inhabit expands.

The easiest way to think about the expansion of the universe is to think about the expansion of something simpler, like a balloon.  If for some reason you have a balloon covered in ants, and you inflate it slowly, then the ants that are nose-to-nose (pardon, “antennae-to-antennae”) with each other will barely notice the expansion.  However, the farther two ants are apart, the more the expansion increases the distance between them.  If an ant on one side tries to run to one of her sisters on the far side of the balloon, she may find that the distance between the two of them is increasing faster than she can close that distance.

The distance at which this happens (where the rate at which the distance decreases because of the movement of the ant and the rate at which the distance increases due to the expansion of the balloon) is a kind of “ant horizon”.  Any pair of ants that are already farther apart than this distance can never meet, and any pair closer than this distance may (if they want).  In the picture above, if an ant can run a distance of 2 during the expansion time, then an ant starting at the yellow point could reach the red point, but an ant starting at the green point will always find itself maintaining the same distance from the red point.

The “ant horizon” is a decent enough analog for the edge of the visible universe.  The speed at which the ant runs is described with respect to the part of the balloon it’s presently standing on and the speed at which light travels is with respect to the space it travels through (technically with respect to objects that are “sitting still” in space).  The oldest photons we see are those that have come from just barely on the near side of the distance at which light can’t close the gap.  It’s not that things beyond that distance are moving away faster than light (almost all the galaxies and gas and whatnot are moving slowly with respect to “the balloon”), it’s that the light they emit just isn’t moving fast enough to overcome the expansion.  Light beyond that is still moving at light speed, and it may even be trying to move toward us, but the distance is simply expanding too fast.

Here the analogy breaks down and starts making our intuition incorrect.  When you inflate a balloon the sides are obviously moving apart.  You can use a rule (maybe a tape measure) and a stopwatch and you can say “dudes and dudettes of the physics world, the speed of expansion is ____”.  Even worse, when a balloon expands it expands into the space around it, which begs the question “what is the universe expanding into?“.  But keep in mind, all that physics really talks about is the relationship between things inside of the universe (on the surface of the balloon).  If you draw a picture on the surface of a balloon, then if the balloon is dented somewhere or even turned inside-out, the picture remains the same (all the distances, angles, densities, etc. remain the same).

Point of fact: it may be that the balloon is a completely false metaphor for the universe as a whole, since the best modern measurements indicate that the universe is flat.  That is, rather than being a closed sphere (hypersphere) it just goes forever in every direction.  This means that there is genuinely no way to describe the expansion of the universe in terms of a speed (there’s no “far side of the balloon” to reference).

Posted in -- By the Physicist, Astronomy, Physics, Relativity | 94 Comments