Q: Are some number patterns more or less likely? Are some betting schemes better than others?

Posted on November 29, 2013 by The Physicist

Physicist: First, don’t gamble unless you can be sure you won’t get caught cheating or you enjoy losing money.

Games of chance come in two flavors: “completely random” and “not quite completely random”.  It’s not always obvious which is which, and it often barely matters.  A good way to tell the difference is to imagine showing the game as it presently is to Leonard Shelby (that guy who can’t form new memories from Memento).  If after extensive investigation he always has the same advice (“I don’t know, bet on red?”), then the game is memoryless.  “Memoryless” is a genuine fancy math term, and refers to systems where the future results are unaffected by the past results.

Remember Sammy Jenkins

Leonard Shelby from Memento.  If a game resets and doesn’t “remember” anything, then there’s no overall pattern, and no way to “outsmart” it.  For these games Leonard is on an equal footing with everyone else.

Say there are some folk playing a really simple game called “guess the number”.  You guess a number, roll a die, and if you guessed right you win.  For all its pomp and glitter, this is essentially what gambling is.  Don’t gamble.

Now say that a few rounds have already been played, and on the fourth round a 3 is rolled.  Lenny would experience that fourth round differently than most other people.

The same game as seen by someone without memory (top) and as seen by someone with memory (bottom).

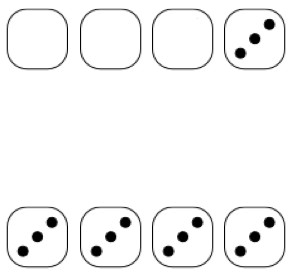
The same series of rounds as seen by someone without memory (top) and as seen by someone with memory (bottom).

Lenny sees a 3 and moves on with his life.  He knows that a 3 is as likely as any other number, so he isn’t surprised.  It’s only those of us burdened with memory who see “patterns” in these random numbers (fun fact: this is called “apophenia“).  Someone who had seen the first rounds churn out a string of 3’s might think that the fourth round will be less likely or more likely to be a 3.  However, assuming that the dice are fair, it turns out that Lenny’s intuition is better than ours; the roll of each of the dice is completely independent all of the other rolls.

The chance of getting these four 3’s in a row is \left(\frac{1}{6}\right)^4 = \frac{1}{1296}.  That’s clearly pretty unlikely, but it’s exactly as unlikely as every other possible combination.  “1, 2, 3, 4” or “2, 6, 5, 5” or whatever else all show up with the same probability.  There are some subtleties in combinatorics, but as long as you keep track of the order it’s fairly straightforward.  “3, 3, 3, 3” is definitely unlikely, but so is every every other possibility.  If the lottery pulled the same number, or a string of consecutive numbers, or some other obvious pattern, it would be surprising but it would be no more or less likely than any other sequence of numbers.  That said, if it keeps happening, then you may want to explore why.  For example, there may be trickery involved.

What we expect to see is what fancy math folk call a “typical sequence“; big jumbles of numbers with no discernible rhyme or reason.  Every string of (fair) rolled dice is equally likely and while randomly emerging “patterns” will occasionally show up, they don’t change the math and can’t be predicted.  Of course, they do make for better stories.

This is from xkcd.  Clearly.

Games like craps or roulette are memoryless, which means that notions like “hot tables” and “runs” are completely baseless.  On the other hand, games like blackjack are not quite memoryless.  Since the cards are pulled from the same shoe if you sit and watch the cards for long enough you can predict which cards will be drawn next slightly better than someone who hasn’t.

Lotteries are also memoryless.  So, assuming the lottery is fair, the only way you can increase your probability of winning is to buy more tickets (but please don’t).  Number order and choice make no difference whatsoever.  Unfortunately, assuming that the lottery is fair is a big assumption, that isn’t necessarily true.  Keep in mind that lotteries, like all organized gambling institutions, are not created so that someone will win, they’re created so that everyone will lose.

If you want to win a lottery, far and away the best way to do it is to set one up yourself (which is illegal almost everywhere there are laws).  Not to put too fine a point on it, but people who run big lotteries and casinos are massive ——-s.  Gambling is seriously bad news, pretty much across the board (the owners do well).

Statistically speaking, this is still a better use for your money.

Statistically speaking, this is a better use for your money than any form of gambling.

There are much better ways to throw away money than playing the lottery.  Before you think about giving away no-strings-attached money to people who don’t need it, consider trying: “cashfetti” cannons, recreating that scene from Indecent Proposal, money origami, lighting cigars, lining animal pens, breaking chopsticks, and eating it to gain it’s power.

A lot of folk have written in asking for mathematically-based gambling advice and, details aside, here it is: Don’t.  The only way to win is not to play.

Posted in -- By the Physicist, Combinatorics, Entropy/Information, Math, Probability | 10 Comments

Q: Why does iron kill stars?

Posted on November 22, 2013 by The Physicist

Physicist: Every now and again a physicist finds themselves in front of a camera and, either through over-enthusiasm or poor editing, is heard to say something that is “less nuanced” than they may have intended.  “Iron kills stars” is one of the classics.

Just to be clear, if you chuck a bunch of iron into a star, you’ll end up with a lot of vaporized iron that you’ll never get back.  The star itself will do just fine.  The Earth is about 1/3 iron (effectively all of that is in the core), but even if you tossed the entire Earth into the Sun, the most you’d do is upset Al Gore.  Probably a lot.

Stars are always in a balance between their own massive weight that tries to crush their cores, and the heat generated by fusion reactions in the core that pushes all that weight back out.  The more the core is crushed, the hotter and denser it gets, and the more the rate of fusion reactions increases (increases the cores rate of “explodingness”), which pushes the bulk of the Star away from the core again.  As long as there’s “fuel” in the core, any attempt to crush it will result in the core pushing back.

Young stars burn hydrogen, because hydrogen is the easiest element to fuse and also produces the biggest bang.  But hydrogen is the lightest element, which means that older stars end up with a bunch of heavier stuff, like carbon and oxygen and whatnot, cluttering up their cores.  But even that isn’t terribly bad news for the star.  Those new elements can also fuse and produce enough new energy to keep the core from being crushed.  The problem is, when heavier elements fuse they produce less energy than hydrogen did.  So more fuel is needed.  Generally speaking, the heavier the element, the less bang-for-the-buck.

The "nuclear binding energy"

The “nuclear binding energy” of a selection of elements by atomic weight.  The height difference gives a rough idea of how much energy is release by fusion.  Notice that there’s a huge jump between, say, hydrogen (H1) and helium (He4), but a much smaller jump between aluminum (Al27) and iron (Fe56).

Iron is where that slows to a stop.  Iron collecting in the core is like ash collecting in a fire.  It’s not that it somehow actively stops the process, but at the same time: it doesn’t help.  Throw wood on a fire, you get more fire.  Throw ash on a fire, you get hot ash.

So, iron doesn’t kill stars so much as it is a symptom of a star that’s about to be done.  Without fuel, the rest of the star is free to collapse the core without opposition, and generally it does.  When there’s a lot of iron being produced in the core, a star probably only has a few hours or seconds left to live.

Of course there are elements heavier than iron, and they can undergo fusion as well.  However, rather than producing energy, these elements require additional energy to be created (throwing liquid nitrogen on a fire, maybe?).  That extra energy (which is a lot) isn’t generally available until the outer layers of the star come crushing down on the core.  The energy of all that falling material drives the fusion rate of the remaining lighter elements way, way, way up (supernovas are super for a reason), and also helps power the creation of the elements that make our lives that much more interesting: gold, silver, uranium, lead, mercury, whatever.

There are more than a hundred known elements, and iron is only #26.  Basically, if it’s heavy, it’s from a supernova.  Long story short: iron doesn’t kill stars, but right before a (large) star dies, it is full of buckets of iron.

Posted in -- By the Physicist, Physics | 21 Comments

Q: According to relativity, things get more massive the faster they move. If something were moving fast enough, would it become a black hole?

Posted on November 13, 2013 by The Physicist

Physicist: Nopers!  Although that would be an amazingly cool super-weapon.

Physics can be pretty complicated, but what makes physics different from lesser sciences, like Calvinball, is that physics has rules that are absolute.  While the consequences can sometimes be difficult to predict (technically, platypi are a direct result of fundamental physical laws), the rules themselves tend to be pretty straightforward.  In the case of relativity there are two big starting rules:

#1)  All of physics works exactly the same whether you’re moving or sitting still.  So, in absolutely every way that counts, there’s no difference.

#2) The speed of a passing light beam is always the same.

There are a lot of bizarre things that fall out of that second rule (generally in not completely obvious ways).  Among them is the fact that the equations Newton figured out for momentum and energy, P=mv and E = \frac{1}{2}mv^2, are actually only approximations.  In particular, the equation for momentum is actually P=\gamma mv.  That \gamma describes a lot of relativistic phenomena.  It’s very close to one for low speeds, which makes P=\gamma mv \approx mv (which is why Newton never noticed it).  The greater the speed, the bigger \gamma becomes, and the more “\gamma m” looks like a bigger mass.  But keep in mind; that speed is relative.  You can only see that “increased mass” in something else, because you can never move relative to yourself.

Values of gamma vs. fraction of light speed. Being close to 1 make it unimportant at low speeds.

Values of gamma vs. fraction of light speed. Being close to 1 at low speeds means that the “error” from relativistic effects is very small.  Apollo 10 is the fastest (Earth relative) any human has ever moved.

So finally, here’s the point:

So long as the particle or object in question isn’t currently slamming into anything that’s moving differently (or “relatively”), then you can just apply rule #1.  No matter how fast or slow something is moving, it will always behave exactly the same way it would if it were sitting still.  So, if you accelerate a rock to 99.99999999% of light speed (or thereabouts), then it will do exactly what a rock at 0% of light speed does: be a rock.  A fast rock, sure, but it wouldn’t suddenly do anything a regular rock wouldn’t.  I’m not knocking rocks, they’re fine and all, it’s just that they’re not black holes, which are terribly exciting.

It turns out that gravity is way more complicated than Newton first proposed.  The same set of theories (special and general relativity) that accurately predicted that fast objects will behave more massive from our “stationary” perspective, also predicted a whole mess of weird things about gravity.  Including the fact that gravity itself always obeys rules #1 and #2.  So if a thing isn’t a black hole when it’s sitting still, then it isn’t a black hole when it’s moving.

Posted in -- By the Physicist, Physics, Relativity | 14 Comments

Q: How do we know that atomic clocks are accurate?

Posted on November 7, 2013 by The Physicist

Physicist: It turns out that there is no way, whatsoever, to look at a single clock and tell whether or not it’s accurate.  A good clock isn’t so much accurate as it consistent.  It takes two clocks to demonstrate consistency, and three or more to find a bad clock.

Left: Might have the right time? Right: Does have the right time.

Left: Might have the right time? Right: Does have the right time.

Just to define the term: a clock is a device that does some predictable physical process, and counts how many times that process is repeated.  For a grandfather clock the process is the swinging of a pendulum, and the counting is done by the escapement.  For an hour glass the process is running out of sand and being flipped over, with the counting done by hand.

A good hour glass can keep time accurate to within a few minutes a day, so sunrise and sunset won’t sneak up on you.  This is more or less the accuracy of the “human clock”.  Balance wheel clocks are capable of accuracies to within minutes per year, which doesn’t sound exciting, but really is.

Minutes per year is accurate enough to do a bunch of historically important stuff.  For example, you can detect that the speed of light isn’t infinite.  It takes 16 minutes for light to cross Earth’s orbit, and we can predict the eclipsing of Jupiter’s moons to within less than 16 minutes.  In fact, telescopes, Jupiter’s moons, and big books full up look-up tables were once used to tell time (mostly on ships at sea).

Minutes per year is enough to determine longitude, which is a big deal.  You can use things like the angle between the north star and the horizon to figure out your latitude (north/south measure), but since the Earth spins there’s no way to know your longitude (east/west measure) without first knowing what time it is.  Alternatively, if you know your longitude and can see the Sun in the sky, then you can determine the time.  It depends on which you are trying to establish.

Trouble crops up when someone clever starts asking things like “what is a second?” or “how do we know when a clock is measuring a second?”.  Turns out: if your clock is consistent enough, then you define what a second is in terms of the clock, and then suddenly your clock is both consistent and “correct”.

An atomic clock uses a quantum process.  The word “quantum” comes from “quanta” which basically means the smallest unit.  The advantage of an atomic clock is that it makes use of the consistency of the universe, and these quanta, to keep consistent time.  Every proton has exactly the same mass, size, charge, etc. as every other proton, but no two pendulums are ever quite the same.  Build an atomic clock anywhere in the universe, and it will always “tick” at the same rate as all of the other atomic clocks.

So, how do we know atomic clocks are consistent?  Get a bunch of different people to build the same kind of clock several times, and then see if they agree with each other.  If they all agree very closely for a very long time, then they’re really consistent.  For example, if you started up a bunch of modern cesium atomic clocks just after the Big Bang, they’d all agree to within about a minute and a half today.  And that’s… well that’s really consistent.

In fact, that’s a lot more consistent than the clock that is the Earth.  The process the Earth repeats is spinning around, and it’s counted by anyone who bothers to wake up in the morning.  It turns out that the length of the day is substantially less consistent than the groups of atomic clocks we have.  Over the lifetime of the Earth, a scant few billion years, the length of the day has slowed down from around 10 hours to 24.  That’s not just inconsistent, that’s basically broken (as far as being a clock is concerned).

jhg

Atomic clocks are a far more precise way of keeping track of time than the length of the day (the turning of the Earth).

So today, one second is no longer defined as “there are 86,400 seconds in one Earth-rotation”.  One second is now defined as “the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom”, which is what most atomic clocks measure.

The best clocks today are arguably a little too good.  They’re accurate enough to detect the relativistic effects of walking speed.  I mean, what good is having a super-watch if carrying it around ruins its super-accuracy?  Scientists use them for lots of stuff, like figuring out how fast their neutrino beams are going from place to place.  But the rest of us mostly use atomic clocks for GPS, and even GPS doesn’t require that many.  Unless 64 is “many”.

That all said: If you have one clock, there’s no way to tell if it’s accurate.

If you have two, either they’re both good (which is good), or one or both of them aren’t.  However, there’s no way to know which is which.

With 3 or more clocks, as long as at least a few of them agree very closely, you can finally know which of your clocks are “right”, or at least working properly, and which are broken.

That philosophy is at the heart of science in general.  And why “repeatable science” is so important and “anecdotal evidence” is haughtily disregarded in fancy science circles.  If it can’t be shown repeatedly, it can’t be shown to be a real, consistent, working thing.

Posted in -- By the Physicist, Experiments, Logic, Philosophical, Physics | 12 Comments

Q: “i” had to be made up to solve the square root of negative one. But doesn’t something new need to be made up for the square root of i?

Posted on October 30, 2013 by The Physicist

Physicist: The beauty of complex numbers (numbers that involve i) is that the answer to this question is a surprisingly resounding: nopers.

The one thing that needs to be known about i is that, by definition, i^2=-1.  Other than that it behaves like any other number or variable.  It turns out that the square root is \sqrt{i} = \frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}}.  You can check this the same way that you can check that 2 is the square root of 4: you square it.

\begin{array}{ll}\left(\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}}\right)^2\\[2mm]=\left(\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}}\right)\\[2mm]=\frac{1}{\sqrt{2}}\left(1+i\right)\frac{1}{\sqrt{2}}\left(1+i\right)\\[2mm]=\frac{1}{2}\left(1+i\right)\left(1+i\right)\\[2mm]=\frac{1}{2}\left(1+i+i+i^2\right)\\[2mm]=\frac{1}{2}\left(1+i+i-1\right)\\[2mm]=\frac{1}{2}\left(2i\right)\\=i\end{array}

And like any other square root, the negative, -\frac{1}{\sqrt{2}}-\frac{i}{\sqrt{2}}, is also a solution.  So, i does have a square root, and it’s not even that hard to find it.  No new “super-imaginary” numbers need to be invented.

This isn’t a coincidence.  The complex numbers are “algebraically closed“, which means that no matter how weird a polynomial is, it’s roots are always complex numbers.  The square roots of i, for example, are the solutions of the polynomial 0 = x^2-i.  So, any cube root, any Nth root, any power, any combination, any whatever of any complex number: still a complex number.

That hasn’t stopped mathematicians from inventing new and terrible number systems.  They just didn’t need to in this case.

Posted in -- By the Physicist, Math | 17 Comments

Q: Could the tidal forces of the Sun and Moon be used to generate power directly?

Posted on October 22, 2013 by The Physicist

The original question was: If a machine enclosed in a building could, as I think it could, detect the tidal forces of the sun and moon upon the Earth could the effect be used to extract useful energy from those forces and what would the effect be on the motion of the Earth?

Physicist: “Useable” energy; yes.  But probably not too useful.  You can calculate the maximum total energy caused by lunar and solar tides on something the size and mass of a building, and you find that it’s really, really tiny.

To generate power from tidal forces directly, in a self contained building, you’d want to lift something very heavy when the gravity is “turned down”, and then lower it and generate power when gravity is “turned up”.  That difference is not big.  It’s about 1 part in 3 million at best (even less for the Sun).  Unfortunately, motors and generators that are more than 99.99996% efficient just aren’t made, so that tiny “1 part in 3 million” may as well be zero since it won’t cover energy lost to inefficiency.

The approximate relative sizes and distances of the Earth and Moon.

The Earth, Moon, and the space between them (to scale).  This is why you don’t notice the difference in gravity.

A building the size of the Burj Khalifa could generate an absolute maximum of around 100MJ of energy, twice daily (two tides), using perfectly efficient machines.  It would just be a huge block of iron that is lifted and dropped at the right times.  So under unrealistically ideal conditions, such a building could daily provide electricity to the United States for not quite half a millisecond.

However, it is both possible and feasible to harvest the tide for power.  Basically you find a bay with a single small inlet and you put free flow hydroelectric turbines in the inlet to catch the ocean tide flowing in and out.  You don’t have to build a huge weight and a bunch of machines to raise and lower it, you just anchor some turbines on the bottom of a bay.  Much easier.  There are a bunch of these already in use, and they tend to be far more compact and powerful than wind turbines.  Water, being denser, carries a lot more energy and packs a much bigger punch than air.

Ultimately, all of the energy gained from tidal forces has to come from somewhere, and that somewhere is the rotational kinetic energy of the Earth.  So, when you generate power from tides you literally slow the Earth down.  But that slowing isn’t something to worry about.  The oceans, and the crust of the Earth itself, are already doing more than their part.

Right now the “tidal bulge” of the Earth leads the Moon (just because it takes a little time for things to move around), and the effect of this is to slow the rotation of the Earth while speeding up the Moon’s orbit.

Fun fact: the day was once about a third as long, and the Moon was more than ten times closer.

The Earth is stretched slightly by the lunar tidal force.  But the Earth turns, and it and the oceans don’t snap back into shape instantly, so there’s always a little extra mass leading the Moon.  The pull of this extra mass speeds up the Moon in its orbit and slows the turning of the Earth.

Every attempt to harvest energy from the tide comes down to keeping extra mass higher than it “should” be for a little extra time, and this amounts to making the tidal bulge just a tiny bit bigger.  But even if we “captured the tide” along every coast in the world, our efforts would be statistical noise compared to the sloshing of the entire ocean.

Posted in -- By the Physicist, Astronomy, Engineering, Physics | 5 Comments