Physicist: The original statement is often something like, “It takes tens of thousands of years for a photon to get from the core to the surface of the Sun, but only eight minutes to get from the Sun to the Earth”. This is one of those great facts that the cognoscenti love to throw around, like “did you know that we only use 10% of our brains?”. Unfortunately, like the 10% thing, there are details behind this fact that make it somewhat less interesting and ultimately either false or not even wrong.
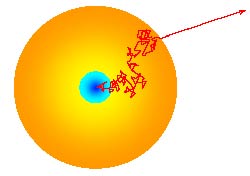
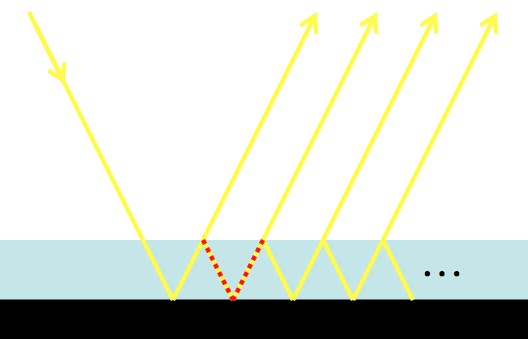
A photon randomly meanders out of the Sun.
The calculation behind the many-thousands-of-years stat goes like this:
-A photon travels, on average, a particular distance, d, before being briefly absorbed and released by an atom, which scatters it in a new random direction.
-Given d and the speed of light, c, you can figure out the average time step and space step size (how often the photon “steps” and how far it “steps” each time).
-The size of the Sun is figured in terms of step size. Some surprisingly tricky math happens, involving “Brownian motion” and probabilities. Finally,
-The average time it would take to get to the surface of the Sun is found.
The math behind this is similar (identical) to the math behind things like Plinko, or the gambler’s ruin. The calculation is a little tricky (which is why it’s sometimes used as an example), but the conclusion is that a photon takes between many thousands and many millions of years to drunkenly wander to the surface of the Sun. If you’re dying of curiosity, then one such calculation is included in the answer gravy (the last part of this post).
However, this result is a little misleading. First, because it makes some subtle mathematical assumptions, and second, because it makes some massive (false) physical assumptions. Inside of the Sun photons are continuously being exchanged, split into many, gathered into one, scattered, and generally not kept in one piece. Rather than thinking of photons in the Sun as being like pinballs bouncing between kicker-like atoms, think of photons as being like over-flowing coffee and the atoms as being like cups.

You can think of the inside of the Sun like this; a bunch of cups overflowing into each other in a giant art thing. It doesn’t make sense to talk about how long it takes for the coffee in the middle-most cup of the art to get out of the art, but it does make sense to talk about how long before half of it is out, or before at least some of it is out.
After being created in a fusion event in the core, the first thing a fresh batch of photons does is get broken up into hundreds of lower energy photons. Talking about how long a photon does anything in the Sun for more than around one nanosecond is a little misleading, because within that time almost every photon in the Sun has been broken apart and/or combined with other photons, leaving them mixed together.
The first tiniest bit of the energy of a photon generated in the core gets to the surface within a couple minutes, and is carried away by photons created there. The many-thousands-of years statistic is useful in that it expresses when about half of a photon’s original energy is bled into space. The last of the photon’s energy is never completely released into space (it’s a “last toothpaste in the tube” sort of thing).
The coffee picture is from here.
Answer Gravy: Just because it’s interesting to see it presented at least one or two ways, at least once, here’s some of the math behind the statistics of random walks and “escapes”. This isn’t the most direct method, but it does the job. Also, photons don’t behave this way, so this is more of a “what if” calculation.
If a particle travels, on average, a distance of Δx in a random direction (50/50 for left/right) every Δt time, then the probability, P(x,t), of the particle being at a particular place at a particular time satisfies the equation:

Now check this out!
![\begin{array}{ll} P(x,t) = \frac{1}{2}P(x+\Delta x,t-\Delta t) + \frac{1}{2}P(x-\Delta x,t-\Delta t) \\[2mm] \Rightarrow P(x,t)-P(x,t-\Delta t)=\frac{1}{2}P(x+\Delta x,t-\Delta t)+\frac{1}{2}P(x-\Delta x,t-\Delta t)-P(x,t-\Delta t) \\[2mm] \Rightarrow P(x,t)-P(x,t-\Delta t)=\frac{1}{2}\left(P(x+\Delta x,t-\Delta t)-P(x,t-\Delta t)\right)-\frac{1}{2}\left(P(x,t-\Delta t)-P(x-\Delta x,t-\Delta t)\right) \\[2mm] \rightarrow \frac{\partial P(x,t)}{\partial t}=\frac{\left(\Delta x\right)^2}{2\Delta t}\frac{\partial^2 P(x,t)}{\partial x^2} \\[2mm] \end{array} \begin{array}{ll} P(x,t) = \frac{1}{2}P(x+\Delta x,t-\Delta t) + \frac{1}{2}P(x-\Delta x,t-\Delta t) \\[2mm] \Rightarrow P(x,t)-P(x,t-\Delta t)=\frac{1}{2}P(x+\Delta x,t-\Delta t)+\frac{1}{2}P(x-\Delta x,t-\Delta t)-P(x,t-\Delta t) \\[2mm] \Rightarrow P(x,t)-P(x,t-\Delta t)=\frac{1}{2}\left(P(x+\Delta x,t-\Delta t)-P(x,t-\Delta t)\right)-\frac{1}{2}\left(P(x,t-\Delta t)-P(x-\Delta x,t-\Delta t)\right) \\[2mm] \rightarrow \frac{\partial P(x,t)}{\partial t}=\frac{\left(\Delta x\right)^2}{2\Delta t}\frac{\partial^2 P(x,t)}{\partial x^2} \\[2mm] \end{array}](//s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D++++P%28x%2Ct%29+%3D+%5Cfrac%7B1%7D%7B2%7DP%28x%2B%5CDelta+x%2Ct-%5CDelta+t%29+%2B+%5Cfrac%7B1%7D%7B2%7DP%28x-%5CDelta+x%2Ct-%5CDelta+t%29+%5C%5C%5B2mm%5D++++%5CRightarrow+P%28x%2Ct%29-P%28x%2Ct-%5CDelta+t%29%3D%5Cfrac%7B1%7D%7B2%7DP%28x%2B%5CDelta+x%2Ct-%5CDelta+t%29%2B%5Cfrac%7B1%7D%7B2%7DP%28x-%5CDelta+x%2Ct-%5CDelta+t%29-P%28x%2Ct-%5CDelta+t%29+%5C%5C%5B2mm%5D++++%5CRightarrow+P%28x%2Ct%29-P%28x%2Ct-%5CDelta+t%29%3D%5Cfrac%7B1%7D%7B2%7D%5Cleft%28P%28x%2B%5CDelta+x%2Ct-%5CDelta+t%29-P%28x%2Ct-%5CDelta+t%29%5Cright%29-%5Cfrac%7B1%7D%7B2%7D%5Cleft%28P%28x%2Ct-%5CDelta+t%29-P%28x-%5CDelta+x%2Ct-%5CDelta+t%29%5Cright%29+%5C%5C%5B2mm%5D++++%5Crightarrow+%5Cfrac%7B%5Cpartial+P%28x%2Ct%29%7D%7B%5Cpartial+t%7D%3D%5Cfrac%7B%5Cleft%28%5CDelta+x%5Cright%29%5E2%7D%7B2%5CDelta+t%7D%5Cfrac%7B%5Cpartial%5E2+P%28x%2Ct%29%7D%7B%5Cpartial+x%5E2%7D+%5C%5C%5B2mm%5D++++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0)
This last jump, from a discrete-time process to a continuous process where calculus can be applied, only works when Δx and Δt are very small. In this case the mean free path is Δx = d = 0.01m, which means that at the speed of light, Δt = d/c = 3×10-11s, and  . For a photon that starts at x=0 when t=0, the solution to the equation
. For a photon that starts at x=0 when t=0, the solution to the equation  is:
is: 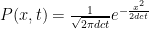 .
.
So, we want to figure out the probability that by some time, T, a particle has passed beyond -R<x<R, where R is the radius of the Sun. Here’s a cute trick: imagine that the Sun keeps going forever, so that nothing special (mathematically difficult) happens at R.
We want to know what the probability is of a photon’s path including x=R (this corresponds to reaching the surface). Notice that if a photon’s path takes it past x=R, then it must have been on the line X=R at some point.
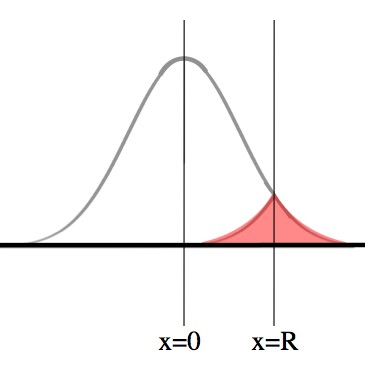
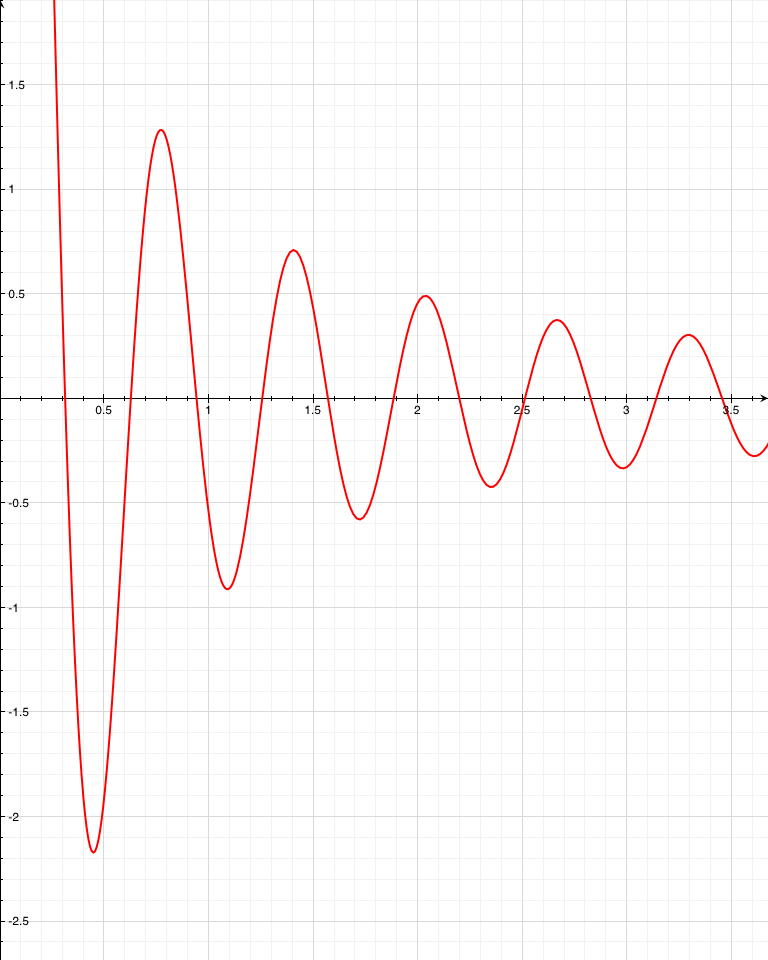
The larger bell curve is the probability of finding the photon at that location after some time t. The pink region is the probability of the photon having gotten to x=R at any time up to T.
Now, since the photon is assumed to have an even chance of going in either direction, then half of the photons that make it to x=R will be on the right of it and half to the left. So, the total probability of making it to x=R is double the probability of being on the far side of x=R. Just so that it looks fancy, let’s say the probability of escape after some time T is 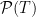 . The whole argument above is a description of why there’s a “2” in front of
. The whole argument above is a description of why there’s a “2” in front of 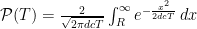 . This can be expressed in terms of the error function,
. This can be expressed in terms of the error function, 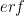 , as
, as  . That re-expression doesn’t change anything, but it does help get everybody on the same page.
. That re-expression doesn’t change anything, but it does help get everybody on the same page.
We can now say that a photon (starting at the center of the Sun, moving at the speed of light, and scattering off of atoms on average every d distance, while hypothetically not being changed by those scatterings) is 50% likely to have escaped the Sun when  , which happens when
, which happens when 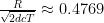 .
.
Plugging in 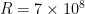 meters,
meters, 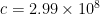 meters/second, and
meters/second, and  meters, you can solve for T and find that T = 1,100,000 years. However, there are different mean free distances in different parts of the Sun (due mostly to different densities), which makes that whole last calculation much more difficult (or you can just run a quick computer simulation). Different people will run through this calculation (or something similar) and get wildly different amounts of time because we may have been using different mean free distance. These folk seem to think the “true time”, taking into account what we know about densities in the Sun, should be somewhere in the 100 thousand year range. But again; keep in mind that actual photons don’t behave this way.
meters, you can solve for T and find that T = 1,100,000 years. However, there are different mean free distances in different parts of the Sun (due mostly to different densities), which makes that whole last calculation much more difficult (or you can just run a quick computer simulation). Different people will run through this calculation (or something similar) and get wildly different amounts of time because we may have been using different mean free distance. These folk seem to think the “true time”, taking into account what we know about densities in the Sun, should be somewhere in the 100 thousand year range. But again; keep in mind that actual photons don’t behave this way.
If you’ve read this far, you may be interested in where there were errors in the big calculation. “Jumping to calculus” introduces a tiny, tiny error, but that decreases rapidly if Δx and Δt are small compared to the scale of the problem (e.g., Δt = 3×10-11 seconds vs. T = 1.1 million years). Also, I’ve ignored the fact that 1) passing -R also means escaping the Sun, and 2) the Sun is a sphere and not a line segment. What I very, very subtly did was “project” the random movement of the photon onto the radial direction, and then only keep track of that direction (“radial” = “out from the center”). This has the effect of changing the  equation. This new form can be approximated by varying d with x. One effect is a “bump” near x=0 that makes it hard to drift back to the exact center, but throughout the region where the photons spend most of their time the effect is mostly just a replacement of d by
equation. This new form can be approximated by varying d with x. One effect is a “bump” near x=0 that makes it hard to drift back to the exact center, but throughout the region where the photons spend most of their time the effect is mostly just a replacement of d by  . I’ve also ignored the time spent being absorbed, which is the same as assuming that the Sun’s index of refraction is 1.
. I’ve also ignored the time spent being absorbed, which is the same as assuming that the Sun’s index of refraction is 1.
Overall the errors introduced are smaller than the errors introduced by the range in different quoted values of d (and the fact that it’s assumed to be constant). Still, it involves some cute math.