Q: What are quasi-particles? Why do phonons and photons have such similar names?

Posted on July 22, 2013 by The Physicist

Physicist: Prefixes like “quasi-“, “psuedo-“, and sometimes “meta-” are basically used to mean “sorta like… but different… you know?”.  Quasiparticles behave like particles in a few fairly important ways, but aren’t actual particles at all.  The most important way, and what makes them look like particles, is that they are discrete, are persistent (stable enough to stick around for at least a little while), and are quantized.  “Quantized” means, in particular, that each quasi-particle of a particular kind is identical.  Generally speaking, a quasiparticle is as small as it can possibly get.

Whirlpools are a good every-day almost-quasiparticle to keep in mind as an example.  While they are generally discrete and persistent (if you have one whirlpool, then in another second you’ll probably still have one whirlpool), they’re not quantized because every whirlpool is different.  No particle physicist in their right mind would call a whirlpool a quasiparticle, but the idea is about right.

vortices

Right: Tornadoes and whirlpools are a lot like quasi-particles. They’re not actual “things”, they’re just “conserved effects”.  Left: magnetic vortices forced into a type 2 superconductor are basically tiny “electron tornadoes”.  These “flux tubes” are legitimate quasi-particles.

Quasiparticles show up a lot when there’s some reason for a particular effect to be conserved, and can be quantized in some useful sense.  For example, magnetic vortex tubes (“flux tubes”) in super conductors aren’t actual things (not particles), but they are persistent, quantized, and are clearly discrete.  They appear in type 2 superconductors, which naturally expel magnetic fields, when you turn up the strength of a nearby magnet high enough to “break through”.  Groups of flux tubes can even have solid and liquid phases, in analogy to regular (actual) matter.

One of the more commonly seen quasi-particles is the “electron hole”, which is just a notably absent electron.

The tiles are real things, and the vacant square is just a conserved

The tiles are real things, but the vacant square is just a conserved effect.  It moves and acts a lot like a particle that can wander around the grid.  It’s a kind of “quasi-tile”.  It’s easier to keep track of the one quasi-tile than to keep track of the 15 real-tiles.

Rather than think about a bunch of negatively charged electrons slowly shouldering past each other in one direction, it’s sometimes useful to thing about a much smaller group of positively charged holes moving quickly in the opposite direction (think of the tile board above, but much bigger, 3-dimensional, and with more vacant tiles).  Turns out that a lot of the relevant math works out the same way.  This notion comes up a lot when talking about diodes, transistors, and semi-conductors in general.

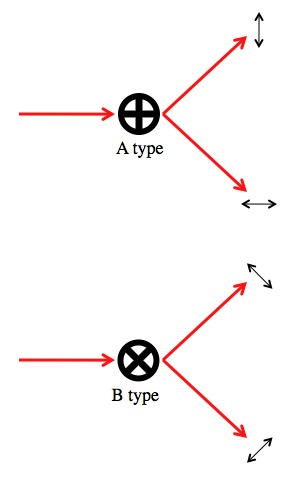
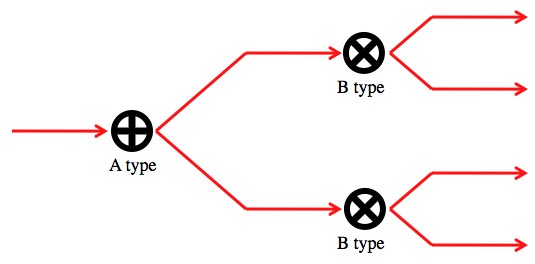
My favorite quasiparticle, the anyon, is a type of tiny electromagnetic vortex that can only appear in very confined, flat plasma fields.  Anyons have properties that should only be found in 2-dimensional particles (which of course don’t exist in our 3-dimensional universe), but as far as they’re concerned, their flat plasma-sheet home is 2-dimensional.  Pushing around anyons is one of the proposed means for building error-resistant quantum computers.

In a crystal, every atom is in the same situation and has identical energy levels.

In a crystal (table salt in this case), every atom is in the same situation and has identical energy levels as some nearby atom.

Phonons are a little more abstract than tornadoes and vacancies.  The electrons in atoms are stuck in separate energy levels, and they can only absorb or emit energy corresponding to differences in those levels.  Turns out that when restricted in a crystal, the energy associated with vibrations of the entire atoms themselves also have this “ladder” of energy levels instead of an effectively continuous set of energy levels (this tendency for energy levels to be discrete and quantized is a big part of where quantum mechanics gets its name).

So each atom has a ladder of “vibrational energy modes”.  The reason it’s important for them to be in a crystal, is that in a crystal all of the atoms are in the same situation and will have identical energy-level-ladders.  This discrete-and-identical set of energy levels is part of why crystals are hard and often transparent (that’s not obvious, it’s just an interesting fact).

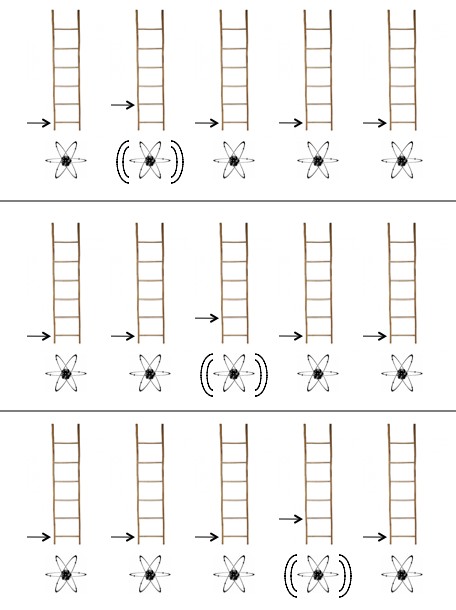
A string of atoms in their ground states, with one atoms in an "excited state".

A string of atoms in their ground states, with one atom in an “excited state”.  This little packet of energy stays intact because there are no smaller energy levels to fall into, so it’s free to be passed from one atom to the next.

Now say that an atom is vibrating one level up from the ground state.  Since the only state the energy can drop to is the ground state, this vibration is all-or-nothing.  The atom can’t give away part of the energy and just vibrate a little less.  When the atom does give up its kinetic energy it stops vibrating and an atom next-door picks up that energy (all of that energy) and starts oscillating in turn.

This one-step-up-from-the-ground-state vibration that passes from place to place is called a “phonon”.  The amount of energy in the levels changes depending on exactly how the atoms are held together, so different kinds of crystals will host slightly different phonons, but the basic idea is the same.

“Phonons” were named in analogy to “photons”.  The prefix “photo-” means “light”, and “phono-” means “sound”.  The suffix “-on” means “particle”.  That one isn’t Latin, but it is pretty standard.  Photons are the smallest possible excited states of the electromagnetic field and are the smallest unit of light, while phonons are the smallest possible excited states of the mechanical system made up of atoms in a crystal and are the smallest possible unit of sound.

Posted in -- By the Physicist, Particle Physics, Physics, Quantum Theory | 13 Comments

The nuptial effect

Posted on July 10, 2013 by The Physicist

Every day, on average, 2-3 physicists get married.  On Saturday I’ll be attempting to push that average to as high as 3-4.

This isn't what

It’ll be more like this than not.

So (for our regular readers), there’ll be a longer gap between posts than usual.  The future Mrs. Physicist (technically, her name will be “Dr. Physicist”) would probably prefer that I show up for the ceremony than stay at home writing about prime numbers and whatnot.

Posted in -- By the Physicist, Combinatorics, Evolution | 23 Comments

Q: How do you prove that the spacetime interval is always the same?

Posted on July 3, 2013 by The Physicist

The original question was: Here’s my current dilemma: how does one rigorously prove the invariance of the space-time interval?  In Taylor & Wheeler’s Spacetime Physics, they basically show one very good example of the invariance, then they instruct the reader to take it as gospel (In case you don’t have their book completely memorized, go here and read pg 22-25). They then use the interval’s invariance to develop the Lorentz transformation.  I did a smidge of research online, but I can’t find an argument that doesn’t use the LT to prove the interval’s invariance. Is it possible to establish the LT without the invariance of the interval?

Physicist: It’s worth noting real quick that this post is aimed at people who have recently taken intro relativity.  That said, if you’re hip with pre-calc, then you’re ready for the basics of special relativity (like this post).

The regular distance, D, between two things located at the points (X1, Y1, Z1) and (X2, Y2, Z2) is found using D2 = (X1-X2)2 + (Y1-Y2)2 + (Z1-Z2)2.  This is basically just the Pythagorean theorem.

But when relativity came along it became important include time, T, along with the the three spacial coordinates, X, Y, and Z.  An “event” is something that happens at a particular place and time.  So, event 1 happens at (X1, Y1, Z1, T1) and event 2 happens at (X2, Y2, Z2, T2).  The timespace interval, S, is found using S2 = (X1-X2)2 + (Y1-Y2)2 + (Z1-Z2)2 – C2(T1-T2)2 = D2 – C2(T1-T2)2, where C is the speed of light and D is the regular (space-only) distance between the events.

What’s tremendously exciting is that not only does the interval stay the same when you change your coordinates through a rotation (regular distance does too), it stays the same when you change your coordinates through motion.  This property is why the spacetime interval is so stunningly useful, but it’s also a little tricky to prove.  You can prove it using only the fact that the speed of light is always the same (regardless of how you’re moving).  What follows isn’t a particularly slick proof, but it works alright.

Things moving at different speeds disagree about where and when things happen.  For example, if someone drives by in a car with a blinking turn-signal, they’d say that each of those blinks are happening in the same place (since the driver is moving with the car, and the lights are built into the car, the signal lights are all stationary to the driver), but someone on the side of the road would say that the blinking light is tracing out a dashed line in space (the blinks happen in different places as the car drives by).  The driver and the pedestrian are said to be in different “reference frames” and, for example, we could accurately say things like “the distance between the blinks in the driver’s frame is zero”.  So, when you’re trying to remember how things can be in different places in different frames or even what frames are, just think: driver/pedestrian.

When considering different coordinate systems we indicate the difference using apostrophes, like this: (X, Y, Z, T) vs. (X’, Y’, Z’, T’).  In (almost) everything that follows the Y and Z coordinates will be ignored, since including them just clutters up the math.  So events will be written “(X, T)”.

There are three cases to consider:

Light-like, S2 = 0

When two events, (X1, T1) and (X2, T2), are “light-like separated” they’re far enough apart and happen long enough apart that a light beam could travel from one to the other, with no time to spare.  Event one could be a photon being emitted, and event two could be that photon hitting something.  So, C = \left|\frac{X_2-X_1}{T_2-T_1}\right| which implies that C|T1-T2| = |X1-X2| which implies that 0 = (X1-X2)2 – C2(T1-T2)2.  But, if the speed of light is always exactly the same, then in a different frame of reference C = \left|\frac{X_2^\prime-X_1^\prime}{T_2^\prime-T_1^\prime}\right|.

Not much to this case.  If things are light-like separated, then the interval is always zero, and 0 = 0.  Done.

Time-like, S2 < 0

How can a squared number be negative?  Don’t worry about it.  It’s never necessary to actually solve for S, so S2 serves just fine.

When two events are “time-like separated” they’re close enough together in space, and far enough apart in time, that by traveling at the right speed you can make both events be in the same place.  The “blinking turn signal” example is a bunch of time-like separated events, and the driver sees them happening in the same place.

In order to use the fact that light travels at the same speed in all reference frames it’s important to include a light beam in your example.  In the “primed coordinates” we make the events happen at the same place at different times, and in the non-primed coordinates the events happen wherever.

Two events linked by a beam of light starting at one, bouncing off of a mirror, and arriving at the second event.

Two events (green and red stars) linked by a beam of light starting at one, bouncing off of a mirror, and arriving at the second.

The total distance traveled by the light beam in the first frame is (by the Pythagorean theorem) 2\sqrt{Y^2 + (X/2)^2}, and at light speed the time it takes to cover this distance can be found with CT = 2\sqrt{Y^2 + (X/2)^2}.

\begin{array}{ll} \Rightarrow C^2T^2=4Y^2+4(X/2)^2\\\Rightarrow C^2T^2=(2Y)^2+X^2\\\Rightarrow -(2Y)^2=X^2-C^2T^2\end{array}

In the second frame (with primed coordinates) the total distance traveled is just 2Y, so \begin{array}{ll} \Rightarrow C^2(T^\prime)^2=4Y^2\\\Rightarrow C^2(T^\prime)^2=(2Y)^2\\\Rightarrow -(2Y)^2=-C^2(T^\prime)^2\\\Rightarrow X^2-C^2T^2=-C^2(T^\prime)^2\end{array}

What this means is that the interval measured in any frame is the same as the interval measured in the frame where the events happen in the same place (and S2 = -(2Y)2).  So, the interval is the same for any frame.

Alternatively, you could make the argument that since Y is unaffected by movement in the X direction, -(2Y)^2=X^2-C^2T^2 is constant since Y doesn’t change.

Space-like, S2 > 0

Two events are “space-like separated” when they’re far enough apart that light doesn’t have time to travel from one to the other.  In time-like separated events there’s a (unique) velocity that you can move at so that both events happen in the same place.  In space-like separated events there’s a (unique) velocity that you can move at so that both events happen at the same time (and in different places).

In “spacetime diagrams” the time direction is up and the space direction is left/right (only one space direction, X, is included).  The statement that light always travels at the same speed becomes the statement that light rays always trace out 45° angles (or it does with properly chosen units, and otherwise it always traces out the same angle).

A rectangle made of light beams. The bottom point emits two light pulses.

A rectangle made of light beams. The bottom point emits two light pulses.  After some amount of time (A and B) each is reflected back, and they meet up at the top corner.

A cute property of the rectangle above is that the diagonals are negatives of each other (when measured with the spacetime interval).  Here comes a proof!

For the green dashed line, S2 = (CB-CA-0)2  – C2(A+B-0)2 = -4C2AB.

For the blue dashed line, S2 = (CB+CA)2  – C2(B-A)2 = 4C2AB.

Now, what elevates this fact from “interesting” to “useful” is the knowledge that time-like separated events preserve the interval (last section), and this new fact about the diagonals can be used to show that the interval stays the same for space-like separated events.

Since the interval between the two events (blue line) is the negative of the

The green lines in these pictures are time-like, and the blue lines are space-like.  Since the interval between the two events (blue line) is the negative of the green line, and since we already know that the green lines have the same interval, then the blue lines must have the same interval.  This means that the interval between two space-like separated events stays the same when you change your frame.

So, the (space-like) interval between two events in a given frame is the negative of the interval between a particular point in the past (which could send a pulse of light to both events) and a particular point in the future (which could receive a pulse of light from both events).  Since these points are time-like separated, we already know that changing frame keeps it the same.  Changing frame doesn’t change the relationship between the four events in terms of how light travels between them, so we get another rectangle and another set of diagonals.  In the new rectangle the time-like diagonals are the same, so the space-like intervals are the same.

Once you’ve got the spacetime interval in your physicist’s toolbox you can almost immediately derive things like time dilation, length contraction, the twin paradox, the list goes on.

Posted in -- By the Physicist, Geometry, Math, Relativity | 19 Comments

Q: Are numbers real?

Posted on June 26, 2013 by The Physicist

Physicist: This question usually comes in the form of “are complex numbers real?” or “are negative numbers real?” or something along those lines.  Turns out you can answer all of these questions at once (if you make up a nice enough definition for what “real” means).

If you think of “realness” in terms of what can be touched, or observed, or measured, then numbers (all kinds of numbers) are clearly not real.  That is, numbers don’t phyiscally exist anywhere.  No beachcomber will ever discover a new number during the practice of their venerated craft.  That said, many people would say that “natural numbers” (which are 1, 2, 3, …) are real in the sense that you can find examples in nature of 3, because you can see (for example) 3 turtles together.  Hence the name: natural numbers.  By the same note, imaginary numbers don’t exist, because you’ll never see i turtles (where i=\sqrt{-1}) in nature.

One, two, three. Three turtles.

One, two, three. Three turtles.

Numbers (math in general really) are all about describing patterns.  Regular numbers are great at describing some things (like how many turtles are around), but there are a lot of patterns in nature that can’t be so easily described and require different kinds of “mathematical objects”, like negative numbers, non-integer numbers, complex numbers, matrices, polynomials, lots of stuff.

“3” seems to be a nice and solid property of the group of turtles in the picture above, and “3” seems pretty “real” as a result.  You can move the turtles around, rename them, paint them, whatever, and you’ll still have 3.  But there’s nothing terribly special about the property of having a certain number of things.  Something like a knot, for example, has properties that are very real but are better described by polynomials.  The “Alexander-Conway polynomial of a knot” stays the same no matter how you change the knot (any change that doesn’t involve cutting).

By the way, this isn’t particularly advanced math and you can learn it yourself!

All of the simplest knots, expressed with the least number of crossings, and the "Riedmeister moves"

All of the simplest knots, expressed with the least number of crossings, and the “Reidemeister moves” which change what a knot looks like, but don’t actually change the knot itself.  Each of these knots (and a lot more) have their own polynomial.

So (and this is the answer), if things in math are “real” because they describe simple properties of things we can see, then natural numbers are no more or less real than polynomials.  The same kind of argument can (probably) be made for all of the other weird structures in mathematics.  It’s just that the number of turtles is a much more obvious property than, say, the topology of a turtle’s plumbing (polynomials or lists of numbers), or its age (real numbers), or its ancestry (graphs).  The quantum mechanical wave function of a turtle (or anything else) is described using complex numbers, because trying to do quantum mechanics without complex numbers is practically impossible.  About as hard as counting turtles without the (obviously “real”) natural numbers.

 

The turtle picture is from here.

Posted in -- By the Physicist, Math, Philosophical | 11 Comments

Q: If time were reversed would things fall up?

Posted on June 18, 2013 by The Physicist

Physicist: Reversing time seems to reverse how things work.  Instead of growing, plants shrink.  Instead of going forward, airplanes fly backward.  And, “intuitively”, instead of falling down, things fall up.  If you have a video of someone jumping into water, then they’ll always fall downward if the video is played normally, and they’ll always fly out of the water and upward if you play the video backward.

If you “rewind time” a couple of seconds you’ll find everything as it was a few seconds ago. So the problem here is that several seconds ago you were not falling from the sky.  If you’ve been walking around here on the surface of the Earth recently, then in reverse-time you’ll still be walking around on Earth.  Just backwards.

So, if you reverse time, things will not fall up.

Turns out that, in general, physical laws can’t tell the difference between time running forward or backward.  The one very big exception is entropy.

As long as things aren't slamming into each other gravity is time-reversal-invariant.

As long as things aren’t slamming into each other gravity is time-reversal-invariant.

The second (and most awesome) law of thermodynamics says that entropy increases in time (technically, it just doesn’t decrease).  Gravitation is a beautiful example of time-symmetry.  So long as the gravitational interaction doesn’t increase entropy, you’d never be able to tell whether or not time is running forward or backward.  A good way for gravity to increase entropy is to make things hit each other.  In that case you’ve got heat being generated, stuff breaking, things flying around, that sort of thing.

So, orbits (which don’t increase entropy) are the same forwards and backwards, but cannonballing into a pool (which increases entropy a lot) only makes sense forwards.

Reversing time does flip the direction that things are moving, but the universe couldn’t possibly care less about how what direction things are moving (this is a less elegant way of describing relativity).  But weirdly, reversing time does not change the direction of acceleration, which the universe does care about.  So an orbiting planet switches direction, but the force of gravity (the acceleration) still points inward.  Isn’t that cool?

Posted in -- By the Physicist, Physics | 21 Comments

Q: Why don’t “cheats” ever work on the uncertainty principle? What’s uncertain in the uncertainty principle?

Posted on June 12, 2013 by The Physicist

Physicist: The Uncertainty Principle is often stated as “the position and momentum of a particle cannot be simultaneously and perfectly measured”.  Mathematically, it’s written as \Delta x \Delta p \ge \frac{\hbar}{2}, which means that the product of the uncertainties in the position, x, and momentum, p, is greater than some (tiny) constant.  But the Uncertainty Principle, rather than being a statement about the techniques we use to make measurements, is about the nature of the particles themselves (this actually applies to everything, not just particles).

The way the uncertainty principle is generally stated it sounds as though our inability to measure the position and momentum simultaneously is a failing of imagination on our parts.  So “cheats” are often conceived to get around the Uncertainty Principle.  The cheat that gave rise to this post is:

An attempt to out-smart the uncertainty principle.

An attempt to out-smart the uncertainty principle.

Say you have two instruments that can very accurately measure the location of a particle and the time when that particle was at that location, and a particle passes by each of them.  Both of them are strictly measuring the position and not momentum, so there shouldn’t be an “uncertainty issue”.  If you take the two (very exact) positions and times, then you can construct the speed of the particle, V=\frac{X_2-X_1}{T_2-T_1}, and thus the momentum, P = MV = M\frac{X_2-X_1}{T_2-T_1}.  Now, even if the first measurement screws up the momentum by accidentally giving the particle a kick during measurement, we still have a mechanism that can tell us the position and momentum immediately after the first measurement with arbitrary precision (which is no good according to the Uncertainty Principle).

However, in quantum mechanics, having something in a definite state does not mean that the results of your measurements will be certain, and this is where the real uncertainty shows up.  In this case you’ll find that if you prepare a string of in-every-way-identical particles and send them past the two detectors one at a time, then the measurements will not measure the same time difference.  Instead they’ll measure a range of different values (each individual measurement will fall within this range), and the size of this range is the uncertainty of the momentum (technically, the standard deviation of this range).

So, the power to do a single accurate measurement doesn’t have much to do with the Uncertainty Principle and doesn’t cause any problems.  But being able to repeat that set of perfect position and momentum measurements, secure in the knowledge (“certain” even) that each trial will have the same result, does violate the Uncertainty Principle.

Answering “why?” there’s no way to perfectly measure momentum and position is a bit more subtle.  Basically, the state of being in a particular position is composed of lots of momentum states, so when the momentum of a given “position state” is measured, you’ll catch any of the large number of momentum states, each of which gives you a different (uncertain) result.  More on that in the answer gravy below.

Answer gravy: This is the same essential point, but with more technical jargon.

The problem with position and momentum is that they are “conjugate variables” which means that their “measurement bases” are related in an obnoxious, Uncertainty making, kind of way.  Conjugate variables are hard to describe, so this sentence is the last time they’ll be mentioned.

This example is to demonstrate that there exists pairs of measurements that must always have uncertainties.

Light can be polarized at any angle.  A “polarizing beam splitter” is a piece of material that causes photons that are polarized in the one way to take one path, and perpendicularly polarized photons to take another path.  Some crystals are surprisingly good at this.

A calcite crystal sorts light based on its polarization.

A calcite crystal sorts light based on its polarization.  Photons polarized “with the grain” go one way, and photons polarized “against the grain” (90° different) go another.  Photons that are polarized somewhere in between have a probability of going either way.

These crystals have molecules that tend to line up in a particular direction, and that gives them weird, direction-dependent, electrical properties which causes different polarizations to interact with them differently.  If a photon is polarized in the same direction that the crystal’s molecules are aligned (“with the grain”), then it will definitely take the first path.  If the photon is polarized perpendicular to the grain, then it will definitely take the second path.  In general, if it’s polarized at some angle θ to the grain, then the probability of it taking the first path is cos2(θ) and the probability of it taking the second path is 1-cos2(θ).  In particular, if it’s polarized at 45° then it has an even chance of going down either path.

Let’s say we’ve got a polarizing beam splitter arranged with the grain pointing straight up (0°).  This beam splitter can perfectly sort photons that are polarized at 0° or 90°.  We’ll call using this beam splitter an “A type” measurement.

Another polarizing beam splitter rotated so that the grain is tilted by 45° can perfectly sort photons polarized at 45° and 135° (or “45° and -45°” if you prefer).  We’ll call using this beam splitter a “B type” measurement.  The difference between the A and B type measurements is they have different “measurement bases”.

An "A type" measurement sends vertical and horizontal photons down different paths, but randomly assigns a path to diagonally polarized photons. The B type measurement does the opposite.

An “A type” measurement sends vertical and horizontal photons down different paths, but randomly assigns a path to diagonally polarized photons. The B type measurement does the opposite.

Now, lets say you create a set up to do an A type measurement, followed by a B type measurement.

This set up should do both types of measurements on a photon coming from the left.

This set up should do both types of measurements on a photon coming from the left by looking at what path it exits through.

But here’s the problem: the vertical polarization state, |\uparrow\rangle, is an equal combination of the diagonal states, |\nearrow\rangle and |\nwarrow\rangle, and each of those diagonal states are an equal combination of the vertical and horizontal states, |\uparrow\rangle and |\rightarrow\rangle.  This means that a vertically polarized photon will have a definite result from the A type measurement, but a completely random measurement from the B type measurement (either path with a 50/50 chance).  Similarly, a photon that has a definite result from the B type measurement will have a completely random result from the A type measurement.

So, if you repeat this experiment with a huge number of identically prepared photons, you’ll never be certain which of the four paths it will exit through.  They’ll always exit through at least two of the paths.  This is literally an uncertainty principle (though not one of the big ones, like position/momentum).

However, the source of this “path uncertainty principle” and the position/momentum Uncertainty Principle stem from the same source.  Here you can’t be sure of the measurement, because the states that give you a definite result for one measurement is made of a combination of states that give uncertain results for the other measurement.  E.g., the vertical state is exactly the same as a combination of the diagonal states, so it’ll give a definite result for the A type measurement, but since it’s some of both of the diagonal states it will yield either of the possible results from the B type measurement.

Position measurements and momentum measurements are similar.  The state of being at a particular position, a “position state”, is the same as a huge combination of momentum states that have different momenta (momentums?).  In exactly the same way, a particular momentum state is exactly the same as a particular combination of position states (this is not obvious, so don’t stress).  So, if you’ve set things up so that you have a definite, “certain”, result for one, then you’ve set things up so that you don’t have a definite result for the other, just like with the whole “A type / B type photon thingy”.  Unfortunately, there’s just no way around that.

 

The pencil picture is from here.

Posted in -- By the Physicist, Physics, Probability, Quantum Theory | 2 Comments