Ask a Mathematician / Ask a Physicist

Q: Do the past and future exist? If they do, is the future determined and what does that mean for quantum randomness?

Posted on June 6, 2013 by The Physicist

Physicist: This is a difficult question to even ask, because the word “exist” carries with it some “time-based assumptions”. For example, if you ask “does the Colossus of Rhodes exist?” the correct answer should be “it did, but it doesn’t now.

The problem with the way the word “exists” is used is that it implies “now”. So, in that sense: no, the past and future don’t exist (by definition). But big issues start coming into play when you consider that in relativity (which has given us a much more solid and nuanced understanding of time and space) what “now” is depends on how you’re physically moving. There’s a post here that goes into exactly why.

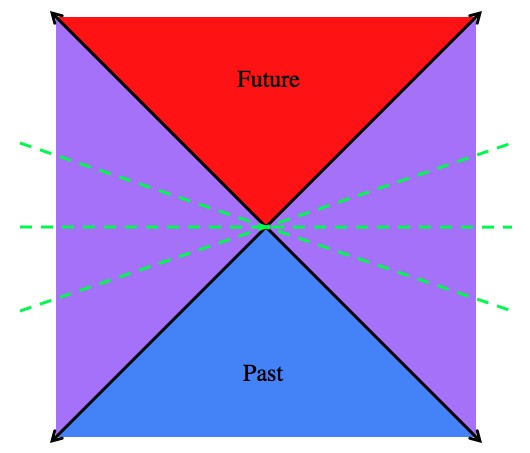
Time points up and space points left/right.

“Here and now” is the center of this picture. Everything in the bottom blue triangle is definitely in the past, and everything in the top red triangle is definitely in the future. But things in the purple triangles can be either in the past or future or present, depending on how fast you’re moving. The dashed lines are examples of different “nows”. In this diagram time points up and space points left/right.

Here’s what’s interesting with that: if we can say that the present and all those things that are happening now exist (regardless of who’s “now” we’re using), then we can show that the past and future exist in the exact same sense.

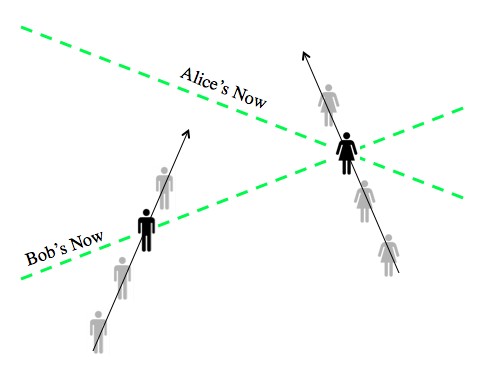
By moving fast, and in different directions, Alice and Bob have different “nows”. In this diagram Bob’s now includes Alice at some particular moment, but for Alice that moment happens at the same time (same “now”) as a time in Bob’s future. Like in the last diagram, time is up and space is left/right.

Again, if we define things that are can be found “right now” as existing, and we don’t care whose notion of “right now”we use, then the future and past exist in exactly the same way that the present exists.

It seems as though what’s going on in the present is somehow important and “more real” than what happened in the past. But consider this; we never interact with other things in the present. Because no effect can travel faster than light the best we can hope for is to interact with the recent past of other things. For example, since light travels about 1 foot per nanosecond, the screen you’re seeing now is really the screen as it was a nanosecond or two ago. Hard to notice. In relativity everything (all the laws, cause and effect, that sort of thing) is “local”, which means that the only thing that matters to what’s happening here and now is everything in the “past light cone” of here and now. That’s the blue bottom triangle of the top picture.

What’s happening now in other places is totally disconnected. For example, Alpha Centauri is about 4 light years away, and while things are certainly happening there “right now”, it won’t matter to us at all for another four years. Even though those events are happening now, they’re exactly as indeterminate and hard to guess as the things that will happen in the future. The point is that “now” does extend throughout the universe, but that doesn’t physically mean anything, or have an actual effect on anything.

So if things in the past and future exist in the exact same way that things in the present exist, then doesn’t that mean that they’re fixed? If my future is the past for someone else who’s around right now (and necessarily moving very fast like in the last diagram), then does that somehow determine the future? The answer to that question is: it doesn’t matter, but for two interesting reasons.

First, if you consider someone else who’s around “now”, then they’re not in your past light cone and they’re not in your’s (in the top diagram the “nows” are always in the purple regions). That means that, for example, some of Bob’s future will be in Alice’s past, but neither of them can know what that future holds until they wait a while. Bob has to wait until he’s “in the future”, and Alice has to wait for the signal delay before she can know anything. Either way, the events of Bob’s future are unknowable regardless of who (in Bob’s present) is asking. The future is a lock and the only key is patience.

Answer gravy: The second reason it doesn’t matter if the future exists involves a quick jump into quantum mechanics (and arguably should have involved a jump into a new, separate post). There could be an issue with the future existing (and thus being predetermined) because that flies in the face of quantum randomness which basically says (and this is glossing over a lot) that the result of an experiment doesn’t exist until after that experiment is done. This is embodied by Bell’s theorem, which is a little difficult to grasp. So Schrödinger’s Cat is both alive and dead until its box is opened. But if, in the future, the box has already been opened and the Cat is found to be alive, then the Cat was always alive. Things like superposition and all of the usual awesomeness of quantum mechanics go away.

But, before you stress out and start researching to try to really understand the problem in that last paragraph: don’t. Turns out there isn’t an issue. Even if the future does exist, it doesn’t mean that events are set in stone in any useful or important way. In the (poorly named) Many Worlds interpretation of quantum mechanics, every thing that can happen does, and those many ways for things to happen are described by a (fantastically complicated) quantum wave function. That wave function is set in stone by an extant future, but that doesn’t tell you exactly what will happen. In the case of Schrödinger’s Cat, the Cat is in a super-position of both alive and dead before the box is opened, and afterward it’s still alive and dead but the observer is “caught up” in the super-position.

The super-position of states after the box is opened: Schrdoinger sad about his dead cat

The super-position of states after the box is opened: Schrödinger sad about his dead cat and Schrödinger happy about his still living cat.

Before the box is opened we can say that, in the future, we will definitely be in a particular super-position of both happy (because of the cute living cat) and horrified (because of the gross dead cat). However, that doesn’t actually predict which result you’ll experience. Technically you’ll experience both.

Posted in -- By the Physicist, Philosophical, Physics, Quantum Theory, Relativity | 52 Comments

Basic math with infinity

Posted on May 31, 2013 by The Physicist

Physicist: Several questions about doing basic math with infinity have been emailed over the years, so here’s a bunch of them! (More can be added later)

Infinity comes in a lot of shapes and flavors. However, the most straightforward infinity that makes the most intuitive sense (for most people) is probably the infinity that “sits at the end of the number line“. $\infty$ is defined as the “value” such that given any number, x, we always have x < $\infty$ . “Value” is in quotes there (‘ ” ” ‘) because infinity isn’t an actual value, it’s more of a place-holder for “bigger than anything else”.

As soon as the word “infinity” is dropped anywhere on the internet the tone suddenly becomes a little… philosophical. So, just to be specific: $\infty$ > x, for any number x, and $\infty$ is assumed to be the unique thing that has that property (Nothing more or less).

$\infty$ + 1 = ?

Like you’d expect, $\infty$ + 1 = $\infty$ . This is because $\infty$ > x-1, for any x, and therefore $\infty$ + 1 > x for any x, and therefore (because $\infty$ is defined to be the only thing with this property), $\infty$ +1 = $\infty$ . This brings up the interesting fact that $\infty$ + 1 is not bigger than $\infty$ (no matter what any second grader might say). They’re the same.

$\infty$ + $\infty$ = ?

$\infty$ again. Pick any number, x, and you find that $\infty$ + $\infty$ > $\infty$ + x/2 > x/2 + x/2 = x. So, $\infty$ + $\infty$ = $\infty$ . This one isn’t too surprising either.

$\infty$ – $\infty$ = ?

This is a bit more nuanced. Your first inclination might be “0”, but keep in mind that that would mean that $\infty$ – $\infty$ = ( $\infty$ + 1) – $\infty$ = 1. The “not-a-number-ness” of infinity means that subtracting it from itself doesn’t make sense, or at the very least, doesn’t have a definitive result.

$\infty$ / $\infty$ = ?

This is just as nuanced. You may think “1”, because you’re probably more reasonable than not. But consider, if that were the case, then: $\infty$ / $\infty$ = ( $\infty$ + $\infty$ )/ $\infty$ = 2. So, again, there’s no definitive result.

Is $\infty$ even or odd?

Something is even if, when divided by two, the result is an integer. But is $\infty$ /2 an integer? $\infty$ is generally considered to not be an integer (or rational, or even irrational), so $\infty$ isn’t generally considered to be either even or odd.

On a case-by-case basis you can sometimes have “disagreeing infinities” and figure out what they equal. For example, $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}\cdots$ involves a positive infinity ( $1+\frac{1}{3}+\frac{1}{5}\cdots$ ) and a negative infinity ( $-\frac{1}{2}-\frac{1}{4}-\frac{1}{6}\cdots$ ), but if you add up the sum one terms at a time you find that it equals ln(2) = 0.6931…

But in general, the operations we freely use with ordinary numbers (addition, subtraction, ) need to be considered very, very carefully before they’re applied to infinities (or even zeros). In fact, mathematicians almost never “plug in $\infty$ “. Instead, they “sneak up” on it using by limits. For example, if you want to figure out what 1/ $\infty$ is, you say “what is the limit as the number x gets arbitrarily large of the function 1/x?”. In this case you can reasonably say that 1/ $\infty$ = 0, but without actually plugging in weird stuff that doesn’t have an actual, numerical, value.

Posted in -- By the Physicist, Math | 16 Comments

Q: What is the Planck length? What is its relevance?

Posted on May 25, 2013 by The Physicist

Physicist: Physicists are among the laziest and most attractive people in the world, and as such don’t like to spend too much time doing real work. In an effort to streamline equations “natural units” are used. The idea behind natural units is to minimize the number of physical constants that you need to keep track of.

For example, Newton’s law of universal gravitation says that the gravitational force between two objects with masses m₁ and m₂, that are separated by a distance r, is $F = \frac{Gm_1m_2}{r^2}$ , where G is the “gravitational constant“. G can be expressed as a lot of different numbers depending on the units used. For example, in terms of meters, kilograms, and seconds: $G = 6.674\times 10^{-11}\frac{m^3}{kg\,s^2}$ .

In terms of miles, pounds, and years: $G = 7.248\times 10^{-6}\frac{mi^3}{lb\,y^2}$ .

In terms of furlongs, femptograms, and fortnights: $G = 3.713\times 10^{-34}\frac{fl^3}{fg\,fn^2}$ .

Point is, by changing the units you change the value of G (this has no impact on the physics, just the units of measurement). So, why not choose units so that G=1, and then ignore it? The Planck units are set up so that G (the gravitational constant), c (the speed of light), $\hbar$ (the reduced Planck constant), and k_B (Boltzmann constant) are all equal to 1. So for example, “E=mc²” becomes “E=m” (again, this doesn’t change things any more than, say, switching between miles and kilometers does).

The “Planck length” is the unit of length in Planck units, and it’s $\ell_P = \sqrt{\frac{\hbar G}{c^3}} = 1.616\times 10^{-35}$ meters. Which is small. I don’t even have a remotely useful way of describing how small that is. Think of anything at all: that’s way, way, way bigger. A hydrogen atom is about 10 trillion trillion Planck lengths across (which, in the pantheon of worldly facts, ranks among the most useless).

Physicists primarily use the Planck length to talk about things that are ridiculously tiny. Specifically; too tiny to matter. By the time you get to (anywhere near) the Planck length it stops making much sense to talk about the difference between two points in any reasonable situation. Basically, because of the uncertainty principle, there’s no useful (physically relevant) difference between the positions of things separated by small enough distances, and the Planck length certainly qualifies. Nothing fundamentally changes at the Planck scale, and there’s nothing special about the physics there, it’s just that there’s no point trying to deal with things that small. Part of why nobody bothers is that the smallest particle, the electron, is about 10²⁰ times larger (that’s the difference between a single hair and a large galaxy). Rather than being a specific scale, The Planck scale is just an easy to remember line-in-the-sand (the words “Planck length” are easier to remember than a number).

That all said (and what was said is: don’t worry about the Planck constant because it’s not important), there are some places on the bleeding edge of physics where the Planck length (or distances of approximately that size) do show up. In particular, it shows up in the “Generalized Uncertainty Principle” (GUP) where it’s inserted basically as a patch to make physics work in some fairly obscure situations (quantum gravity and whatnot). The GUP implies that at a small enough scale it is literally impossible, in all situations, to make a smaller-scale measurement. In the right light this makes it look like maybe spacetime is discrete and comes in “smallest units”, and maybe the universe is like the image on a computer screen (made up of pixels).

How bleeding edge is the GUP? So bleeding edge that there isn’t even a wikipedia article about it. Like a lot of things in string theory (this is an opinion), these sort of patches may prove to be mistakes. So, spacetime may come in discrete chunks, but the most we can say is that those chunks (if they exist) are very, very, very, very small.

You’d never notice (at least, the experiments designed to notice haven’t so far).

Posted in -- By the Physicist, Particle Physics, Physics, Quantum Theory | 41 Comments

Q: What causes friction? (and some other friction questions)

Posted on May 20, 2013 by The Physicist

Physicist: Political conversations with family, for one.

“Friction” is a blanket term to cover all of the wide variety of effects that make it difficult for one surface to slide past another.

There a some chemical bonds (glue is an extreme example), there are electrical effects (like van der waals), and then there are effects from simple physical barriers. A pair of rough surfaces will have more friction than a pair of smooth surfaces, because the “peaks” of one surface can fall into the “valleys” of the other, meaning that to keep moving either something needs to break, or the surfaces would need to push apart briefly.

This can be used in hand-wavy arguments for why friction is proportional to the normal force pressing surfaces together. It’s not terribly intuitive why, but it turns out that the minimum amount of force, F_f, needed to push surfaces past each other (needed to overcome the “friction force”) is proportional to the force, N, pressing those surfaces together. In fact this is how the coefficient of friction, μ, is defined: F_f= μN.

The force required to push this bump “up hill” is proportional to the normal force. This is more or less the justification behind where the friction equation comes from.

The rougher the surfaces the more often “hills” will have to push over each other, and the steeper those hills will be. For most practical purposes friction is caused by the physical roughness of the surfaces involved. However, even if you make a surface perfectly smooth there’s still some friction. If that weren’t the case, then very smooth things would feel kinda oily (some do actually).

Sheets of glass tend to be very nearly perfectly smooth (down to the level of molecules), and most of the friction to be found with glass comes from the subtle electrostatic properties of the glass and the surface that’s in contact with it. But why is that friction force also proportional to the normal force? Well… everything’s approximately linear over small enough forces/distances/times. That’s how physics is done!

That may sound like an excuse, but that’s only because it is.

Q: It intuitively feels like the friction force should be directly proportional to the surface area between materials, yet this is never considered in any practical analysis or application. What’s going on here?

A: The total lack of consideration of surface area is an artifact of the way friction is usually considered. Greater surface area does mean greater friction, but it also means that the normal force is more spread out, and less force is going through any particular region of the surface. These effects happen to balance out.

If you have one pillar the total friction is μN. If you have two pillars each supports half of the weight, and thus exert half the normal force, so the total friction is μN/2 + μN/2 = μN.

Pillars are just a cute way of talking about surface area in a controlled way. The same argument applies to surfaces in general.

Q: If polishing surfaces decreases friction, then why does polishing metal surfaces make them fuse together?

A: Polishing two metal surfaces until they can fuse has to do with giving them both more opportunities to fuse (more of their surfaces can directly contact each other without “peaks and valleys” to deal with), and polishing also helps remove impurities and oxidized material. For example, if you want to weld two old pieces of iron together you need to get all of the rust off first. Pure iron can be welded together, but iron oxide (rust) can’t. Gold is an extreme example of this. Cleaned and polished gold doesn’t even need to be heated, you can just slap two pieces together and they’ll fuse together.

Inertia welders also need smooth surfaces so that the friction from point to point will be constant (you really don’t want anything to catch suddenly, or everyone nearby is in trouble). This isn’t important to the question; it’s just that inertia welders are awesome.

Q: Why does friction convert kinetic energy into heat?

A: The very short answer is “entropy”. Friction involves, at the lowest level, a bunch of atoms interacting and bumping into each other. Unless that bumping somehow perfectly reverses itself, then one atom will bump into the next, which will bump into the next, which will bump into the next, etc.

And that’s essentially what heat is. So the movement of one surface over another causes the atoms in each to get knocked about jiggle. That loss of energy to heat is what causes the surfaces to slow down and stop.

Posted in -- By the Physicist, Physics | 7 Comments

Q: Is fire a plasma? What is plasma?

Posted on May 13, 2013 by The Physicist

Physicist: Generally speaking, by the time a gas is hot enough to be seen, it’s a plasma.

The big difference between regular gas and plasma is that in a plasma a fair fraction of the atoms are ionized. That is, the gas is so hot, and the atoms are slamming around so hard, that some of the electrons are given enough energy to (temporarily) escape their host atoms. The most important effect of this is that a plasma gains some electrical properties that a non-ionized gas doesn’t have; it becomes conductive and it responds to electrical and magnetic fields. In fact, this is a great test for whether or not something is a plasma.

For example, our Sun (or any star) is a miasma of incandescent plasma. One way to see this is to notice that the solar flares that leap from its surface are directed along the Sun’s (generally twisted up and spotty) magnetic fields.

A solar flare as seen in the x-ray spectrum. The material of the flare, being a plasma, is affected and directed by the Sun’s magnetic field. Normally this brings it back into the surface (which is for the best).

We also see the conductance of plasma in “toys” like a Jacob’s Ladder. Spark gaps have the weird property that the higher the current, the more ionized the air in the gap, and the lower the resistance (more plasma = more conductive). There are even scary machines built using this principle. Basically, in order for a material to be conductive there need to be charges in it that are free to move around. In metals those charges are shared by atoms; electrons can move from one atom to the next. But in a plasma the material itself is free charges. Conductive almost by definition.

Jacob's Ladder; for children of all ages

A Jacob’s Ladder. The electricity has an easier time flowing through the long thread of highly-conductive plasma than it does flowing through the tiny gap of poorly-conducting air.

As it happens, fire passes all these tests with flying colors. Fire is a genuine plasma. Maybe not the best plasma, or the most ionized plasma, but it does alright.

Because the flame has a bunch of free charged particles it is pushed and pulled by

The free charges inside of the flame are pushed and pulled by the electric field between these plates, and as those charged particles move they drag the rest of the flame with them.

Even small and relatively cool fires, like candle flames, respond strongly to electric fields and are even pretty conductive. There’s a beautiful video here that demonstrates this a lot better than this post does.

The candle picture is from here, and the Jacob’s ladder picture is from here.

Posted in -- By the Physicist, Physics | 22 Comments

Q: Why are determinants defined the weird way they are?

Posted on May 6, 2013 by The Physicist

Physicist: This is a question that comes up a lot when you’re first studying linear algebra. The determinant has a lot of tremendously useful properties, but it’s a weird operation. You start with a matrix, take one number from every column and multiply them together, then do that in every possible combination, and half of the time you subtract, and there doesn’t seem to be any rhyme or reason why. This particular math post will be a little math heavy.

If you have a matrix, ${\bf M} = \left(\begin{array}{cccc}a_{11} & a_{21} & \cdots & a_{n1} \\a_{12} & a_{22} & \cdots & a_{n2} \\\vdots & \vdots & \ddots & \vdots \\a_{1n} & a_{2n} & \cdots & a_{nn}\end{array}\right)$ , then the determinant is $det({\bf M}) = \sum_{\vec{p}}\sigma(\vec{p}) a_{1p_1}a_{2p_2}\cdots a_{np_n}$ , where $\vec{p} = (p_1, p_2, \cdots, p_n)$ is a rearrangement of the numbers 1 through n, and $\sigma(\vec{p})$ is the “signature” or “parity” of that arrangement. The signature is (-1)^k, where k is the number of times that pairs of numbers in $\vec{p}$ have to be switched to get to $\vec{p} = (1,2,\cdots,n)$ .

For example, if ${\bf M} = \left(\begin{array}{ccc}a_{11} & a_{21} & a_{31} \\a_{12} & a_{22} & a_{32} \\a_{13} & a_{23} & a_{33} \\\end{array}\right) = \left(\begin{array}{ccc}4 & 2 & 1 \\2 & 7 & 3 \\5 & 2 & 2 \\\end{array}\right)$ , then

$\begin{array}{ll}det({\bf M}) \\= \sum_{\vec{p}}\sigma(\vec{p}) a_{1p_1}a_{2p_2}a_{3p_3} \\=\left\{\begin{array}{ll}\sigma(1,2,3)a_{11}a_{22}a_{33}+\sigma(1,3,2)a_{11}a_{23}a_{32}+\sigma(2,1,3)a_{12}a_{21}a_{33}\\+\sigma(2,3,1)a_{12}a_{23}a_{31}+\sigma(3,1,2)a_{13}a_{21}a_{32}+\sigma(3,2,1)a_{13}a_{22}a_{31}\end{array}\right.\\=a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}\\= 4 \cdot 7 \cdot 2 - 4 \cdot 2 \cdot 3 - 2 \cdot 2 \cdot 2 +2 \cdot 2 \cdot 1 + 5 \cdot 2 \cdot 3 - 5 \cdot 7 \cdot 1\\=23\end{array}$

Turns out (and this is the answer to the question) that the determinant of a matrix can be thought of as the volume of the parallelepiped created by the vectors that are columns of that matrix. In the last example, these vectors are $\vec{v}_1 = \left(\begin{array}{c}4\\2\\5\end{array}\right)$ , $\vec{v}_2 = \left(\begin{array}{c}2\\7\\2\end{array}\right)$ , and $\vec{v}_3 = \left(\begin{array}{c}1\\3\\2\end{array}\right)$ .

The parallelepiped created by the vectors a, b, and c.

Say the volume of the parallelepiped created by $\vec{v}_1, \cdots,\vec{v}_n$ is given by $D\left(\vec{v}_1, \cdots, \vec{v}_n\right)$ . Here come some properties:

1) $D\left(\vec{v}_1, \cdots, \vec{v}_n\right)=0$ , if any pair of the vectors are the same, because that corresponds to the parallelepiped being flat.

2) $D\left(a\vec{v}_1,\cdots, \vec{v}_n\right)=aD\left(\vec{v}_1,\cdots,\vec{v}_n\right)$ , which is just a fancy math way of saying that doubling the length of any of the sides doubles the volume. This also means that the determinant is linear (in each column).

3) $D\left(\vec{v}_1+\vec{w},\cdots, \vec{v}_n\right) = D\left(\vec{v}_1,\cdots, \vec{v}_n\right) + D\left(\vec{w},\cdots, \vec{v}_n\right)$ , which means “linear”. This works the same for all of the vectors in $D$ .

Check this out! By using these properties we can see that switching two vectors in the determinant swaps the sign.

$\begin{array}{ll} D\left(\vec{v}_1,\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right)\\ =D\left(\vec{v}_1,\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right)+D\left(\vec{v}_1,\vec{v}_1, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 1}\\ =D\left(\vec{v}_1,\vec{v}_1+\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 3} \\ =D\left(\vec{v}_1,\vec{v}_1+\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right)-D\left(\vec{v}_1+\vec{v}_2,\vec{v}_1+\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 1} \\ =D\left(-\vec{v}_2,\vec{v}_1+\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 3} \\ =-D\left(\vec{v}_2,\vec{v}_1+\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 2} \\ =-D\left(\vec{v}_2,\vec{v}_1, \vec{v}_3\cdots, \vec{v}_n\right)-D\left(\vec{v}_2,\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 3} \\ =-D\left(\vec{v}_2,\vec{v}_1, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 1} \end{array}$

4) $D\left(\vec{v}_1,\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right)=-D\left(\vec{v}_2,\vec{v}_1, \vec{v}_3\cdots, \vec{v}_n\right)$ , so switching two of the vectors flips the sign. This is true for any pair of vectors in D. Another way to think about this property is to say that when you exchange two directions you turn the parallelepiped inside-out.

Finally, if $\vec{e}_1 = \left(\begin{array}{c}1\\0\\\vdots\\0\end{array}\right)$ , $\vec{e}_2 = \left(\begin{array}{c}0\\1\\\vdots\\0\end{array}\right)$ , … $\vec{e}_n = \left(\begin{array}{c}0\\0\\\vdots\\1\end{array}\right)$ , then

5) $D\left(\vec{e}_1,\vec{e}_2, \vec{e}_3\cdots, \vec{e}_n\right) = 1$ , because a 1 by 1 by 1 by … box has a volume of 1.

Also notice that, for example, $\vec{v}_2 = \left(\begin{array}{c}v_{21}\\v_{22}\\\vdots\\v_{2n}\end{array}\right) = \left(\begin{array}{c}v_{21}\\0\\\vdots\\0\end{array}\right)+\left(\begin{array}{c}0\\v_{22}\\\vdots\\0\end{array}\right)+\cdots+\left(\begin{array}{c}0\\0\\\vdots\\v_{2n}\end{array}\right) = v_{21}\vec{e}_1+v_{22}\vec{e}_2+\cdots+v_{2n}\vec{e}_n$

Finally, with all of that math in place,

$\begin{array}{ll} D\left(\vec{v}_1,\vec{v}_2, \cdots, \vec{v}_n\right) \\ = D\left(v_{11}\vec{e}_1+v_{12}\vec{e}_2+\cdots+v_{1n}\vec{e}_n,\vec{v}_2, \cdots, \vec{v}_n\right) \\ = D\left(v_{11}\vec{e}_1,\vec{v}_2, \cdots, \vec{v}_n\right) + D\left(v_{12}\vec{e}_2,\vec{v}_2, \cdots, \vec{v}_n\right) + \cdot + D\left(v_{1n}\vec{e}_n,\vec{v}_2, \cdots, \vec{v}_n\right) \\= v_{11}D\left(\vec{e}_1,\vec{v}_2, \cdots, \vec{v}_n\right) + v_{12}D\left(\vec{e}_2,\vec{v}_2, \cdots, \vec{v}_n\right) + \cdot + v_{1n}D\left(\vec{e}_n,\vec{v}_2, \cdots, \vec{v}_n\right) \\ =\sum_{j=1}^n v_{1j}D\left(\vec{e}_j,\vec{v}_2, \cdots, \vec{v}_n\right) \end{array}$

Doing the same thing to the second part of D,

$=\sum_{j=1}^n\sum_{k=1}^n v_{1j}v_{2k}D\left(\vec{e}_j,\vec{e}_k, \cdots, \vec{v}_n\right)$

The same thing can be done to all of the vectors in D. But rather than writing n different summations we can write, $=\sum_{\vec{p}}\, v_{1p_1}v_{2p_2}\cdots v_{np_n}D\left(\vec{e}_{p_1},\vec{e}_{p_2}, \cdots, \vec{e}_{p_n}\right)$ , where every term in $\vec{p} = \left(\begin{array}{c}p_1\\p_2\\\vdots\\p_n\end{array}\right)$ runs from 1 to n.

When the $\vec{e}_j$ that are left in D are the same, then D=0. This means that the only non-zero terms left in the summation are rearrangements, where the elements of $\vec{p}$ are each a number from 1 to n, with no repeats.

All but one of the $D\left(\vec{e}_{p_1},\vec{e}_{p_2}, \cdots, \vec{e}_{p_n}\right)$ will be in a weird order. Switching the order in D can flip sign, and this sign is given by the signature, $\sigma(\vec{p})$ . So, $D\left(\vec{e}_{p_1},\vec{e}_{p_2}, \cdots, \vec{e}_{p_n}\right) = \sigma(\vec{p})D\left(\vec{e}_{1},\vec{e}_{2}, \cdots, \vec{e}_{n}\right)$ , where $\sigma(\vec{p})=(-1)^k$ , where k is the number of times that the e’s have to be switched to get to $D(\vec{e}_1, \cdots,\vec{e}_n)$ .

So,

$\begin{array}{ll} det({\bf M})\\ = D\left(\vec{v}_{1},\vec{v}_{2}, \cdots, \vec{v}_{n}\right)\\ =\sum_{\vec{p}}\, v_{1p_1}v_{2p_2}\cdots v_{np_n}D\left(\vec{e}_{p_1},\vec{e}_{p_2}, \cdots, \vec{e}_{p_n}\right) \\ =\sum_{\vec{p}}\, v_{1p_1}v_{2p_2}\cdots v_{np_n}\sigma(\vec{p})D\left(\vec{e}_{1},\vec{e}_{2}, \cdots, \vec{e}_{n}\right) \\ =\sum_{\vec{p}}\, \sigma(\vec{p})v_{1p_1}v_{2p_2}\cdots v_{np_n} \end{array}$

Which is exactly the definition of the determinant! The other uses for the determinant, from finding eigenvectors and eigenvalues, to determining if a set of vectors are linearly independent or not, to handling the coordinates in complicated integrals, all come from defining the determinant as the volume of the parallelepiped created from the columns of the matrix. It’s just not always exactly obvious how.

For example: The determinant of the matrix ${\bf M} = \left(\begin{array}{cc}2&3\\1&5\end{array}\right)$ is the same as the area of this parallelogram, by definition.

The parallelepiped (in this case a 2-d parallelogram) created by (2,1) and (3,5).

Using the tricks defined in the post:

$\begin{array}{ll} D\left(\left(\begin{array}{c}2\\1\end{array}\right),\left(\begin{array}{c}3\\5\end{array}\right)\right) \\[2mm] = D\left(2\vec{e}_1+\vec{e}_2,3\vec{e}_1+5\vec{e}_2\right) \\[2mm] = D\left(2\vec{e}_1,3\vec{e}_1+5\vec{e}_2\right) + D\left(\vec{e}_2,3\vec{e}_1+5\vec{e}_2\right) \\[2mm] = D\left(2\vec{e}_1,3\vec{e}_1\right) + D\left(2\vec{e}_1,5\vec{e}_2\right) + D\left(\vec{e}_2,3\vec{e}_1\right) + D\left(\vec{e}_2,5\vec{e}_2\right) \\[2mm] = 2\cdot3D\left(\vec{e}_1,\vec{e}_1\right) + 2\cdot5D\left(\vec{e}_1,\vec{e}_2\right) + 3D\left(\vec{e}_2,\vec{e}_1\right) + 5D\left(\vec{e}_2,\vec{e}_2\right) \\[2mm] = 0 + 2\cdot5D\left(\vec{e}_1,\vec{e}_2\right) + 3D\left(\vec{e}_2,\vec{e}_1\right) + 0 \\[2mm] = 2\cdot5D\left(\vec{e}_1,\vec{e}_2\right) - 3D\left(\vec{e}_1,\vec{e}_2\right) \\[2mm] = 2\cdot5 - 3 \\[2mm] =7 \end{array}$