Physicist: The Big Bang is sometimes described as being a white hole. But if you think of a white hole as something that’s the opposite of a black hole, then no: white holes aren’t real.
They show up when you describe a black hole using some weird coordinates, so they’re essentially just a non-real mathematical artifact. However, white holes are a cute idea so they show up a lot in sci-fi. White holes are a mathematical abstraction that necessarily exist in the infinite past. That is to say, if you follow the mathematical model that physicists use, you’ll never have a situation where a white hole exists at the same time as anything else. Its existence happens infinitely long ago.
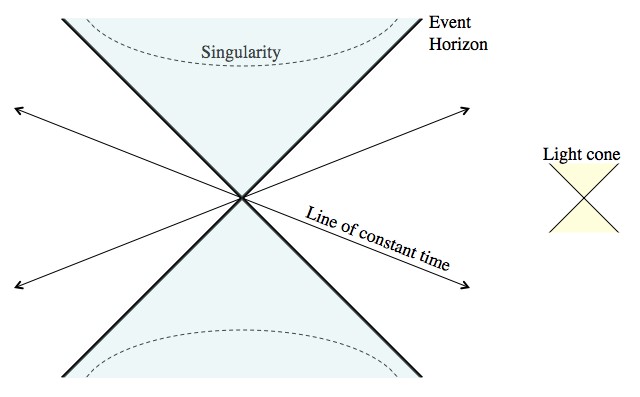
Spacetime gets seriously messed up near and inside of a black hole. To make the math easier, and to help make the situation easier to picture, the Kruskal-Szekeres coordinate system was created.
In this (very unintuitive) diagram straight lines through the center are lines of constant time, with the future roughly up. The event horizon of the black hole is also the infinite future (from an outside perspective it takes forever to fall all the way into a black hole). That should make very little sense, but keep in mind: black holes and weird spacetime go together like Colonial Williamsburg and a lingering sense of disappointment. The black hole’s interior is the upper triangle, the entire universe is the right triangular region and the white hole is the lower region.
The boundary of this lower region is in the infinite past. That is; in this goofy mathematical idealization of a static and eternal black hole, a white hole shows up automatically in the infinite past. One of the issues here is that black holes need to form at some point (in the finite past).
Taking this model completely seriously and assuming that it implies that white holes are real is a little like saying “imagine an infinite robot-godzilla”, and then worrying about where it came from. It’s an abstraction used to think about other things. Physicists love themselves some math, but the love is tempered by the understanding that writing down an equation doesn’t make things real.

Physicists love themselves some math, but (almost always) recognize the scope and limitations of their own equations.
For example, we can talk about the location “North 97°, East 40°”, but that doesn’t make it exist (North 90° is the north pole, the farthest north you can get by definition).
Sci-fi is about the only place you’ll hear people talking about white holes. Whites holes are the opposite of black holes: they spit out matter and energy, they’re impossible to enter, they’re very bright, that sort of thing. In fiction “the opposite of…” is a great way to get weird new ideas (e.g., Bizarro Superman).
The Einstein picture was created here.