Q: Are white holes real?

Posted on April 30, 2013 by The Physicist

Physicist: The Big Bang is sometimes described as being a white hole.  But if you think of a  white hole as something that’s the opposite of a black hole, then no: white holes aren’t real.

They show up when you describe a black hole using some weird coordinates, so they’re essentially just a non-real mathematical artifact.  However, white holes are a cute idea so they show up a lot in sci-fi.  White holes are a mathematical abstraction that necessarily exist in the infinite past.  That is to say, if you follow the mathematical model that physicists use, you’ll never have a situation where a white hole exists at the same time as anything else.  Its existence happens infinitely long ago.

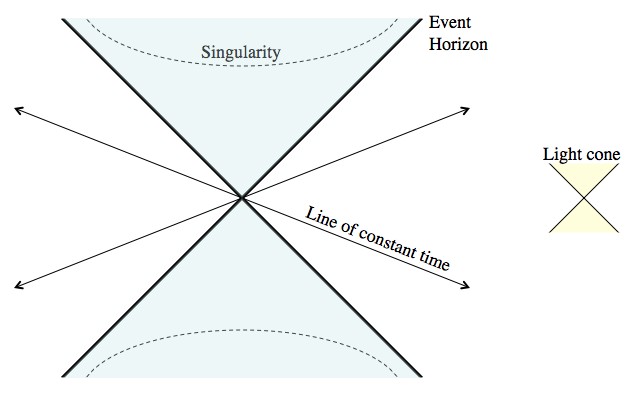
Near and inside of a black hole spacetime

Spacetime gets seriously messed up near and inside of a black hole.  To make the math easier, and to help make the situation easier to picture, the Kruskal-Szekeres coordinate system was created.

In this (very unintuitive) diagram straight lines through the center are lines of constant time, with the future roughly up.  The event horizon of the black hole is also the infinite future (from an outside perspective it takes forever to fall all the way into a black hole).  That should make very little sense, but keep in mind: black holes and weird spacetime go together like Colonial Williamsburg and a lingering sense of disappointment.  The black hole’s interior is the upper triangle, the entire universe is the right triangular region and the white hole is the lower region.

The boundary of this lower region is in the infinite past.  That is; in this goofy mathematical idealization of a static and eternal black hole, a white hole shows up automatically in the infinite past.  One of the issues here is that black holes need to form at some point (in the finite past).

Taking this model completely seriously and assuming that it implies that white holes are real is a little like saying “imagine an infinite robot-godzilla”, and then worrying about where it came from.  It’s an abstraction used to think about other things.  Physicists love themselves some math, but the love is tempered by the understanding that writing down an equation doesn’t make things real.

Physicists love themselves some math.

Physicists love themselves some math, but (almost always) recognize the scope and limitations of their own equations.

For example, we can talk about the location “North 97°, East 40°”, but that doesn’t make it exist (North 90° is the north pole, the farthest north you can get by definition).

Sci-fi is about the only place you’ll hear people talking about white holes.  Whites holes are the opposite of black holes: they spit out matter and energy, they’re impossible to enter, they’re very bright, that sort of thing.  In fiction “the opposite of…” is a great way to get weird new ideas (e.g., Bizarro Superman).

The Einstein picture was created here.

Posted in -- By the Physicist, Astronomy, Math, Physics | 21 Comments

Q: If a photon doesn’t experience time, then how can it travel?

Posted on April 25, 2013 by The Physicist

Physicist: It’s a little surprising this hasn’t been a post yet.

In order to move from one place to another always takes a little time, no matter how fast you’re traveling.  But “time slows down close to the speed of light”, and indeed at the speed of light no time passes at all.  So how can light get from one place to another?  The short, unenlightening, somewhat irked answer is: look who’s asking.

Time genuinely doesn’t pass from the “perspective” of a photon but, like everything in relativity, the situation isn’t as simple as photons “being in stasis” until they get where they’re going.  Whenever there’s a “time effect” there’s a “distance effect” as well, and in this case we find that infinite time dilation (no time for photons) goes hand in hand with infinite length contraction (there’s no distance to the destination).

At the speed of light there's no time to cover any distance, but there's also no distance to cover.

At the speed of light there’s no time to cover any distance, but there’s also no distance to cover.  Left: regular, sub-light-speed movement.  Right: “movement” at light speed.

The name “relativity” (as in “theory of…”) comes from the central tenet of relativity, that time, distance, velocity, even the order of events (sometimes) are relative.  This takes a few moments of consideration; but when you say that something’s moving, what you really mean is that it’s moving with respect to you.

Everything has its own “coordinate frame”.  Your coordinate frame is how you define where things are.  If you’re on a train, plane, rickshaw, or whatever, and you have something on the seat next to you, you’d say that (in your coordinate frame) that object is stationary.  In your own coordinate frame you’re never moving at all.

How zen is that?

Everything is stationary from its own perspective. Only other things move.

Everything is stationary from its own perspective.  Movement is something other things do.  When you describe the movement of those other things it’s always in terms of your notion of space and time coordinates.

The last coordinate to consider is time, which is just whatever your clock reads.  One of the very big things that came out of Einstein’s original paper on special relativity is that not only will different perspectives disagree on where things are, and how fast they’re moving, different perspectives will also disagree on what time things happen and even how fast time is passing (following some very fixed rules).

When an object moves past you, you define its velocity by looking at how much of your distance it covers, according to your clock, and this (finally) is the answer to the question.  The movement of a photon (or anything else) is defined entirely from the point of view of anything other than the photon.

One of the terribly clever things about relativity is that we can not only talk about how fast other things are moving through our notion of space, but also “how fast” they’re moving through our notion of time (how fast is their clock ticking compared to mine).

 

The meditating monk picture is from here.

Posted in -- By the Physicist, Relativity | 364 Comments

Q: What is energy? What is “pure energy” like?

Posted on April 19, 2013 by The Physicist

Physicist: Unfortunately, “pure energy” isn’t really a thing.  Whenever you hear someone talking about something or other being “turned into pure energy”, you’re listening to someone who could stand to be a little more specific about what kind of energy.  And whenever you hear someone talking about something being “made of pure energy”, you’re probably listening to someone who’s mistaken.

Pure energy.

“Pure energy” shows up a lot in fiction, and most sci-fi/fantasy fans have some notion of what it’s like, but it isn’t a thing you’ll find in reality.

Energy comes in a hell of a lot of forms, but they’re all pretty mundane.  For example, when “energy is released” in an explosion (most explosions) that energy mostly takes the form of kinetic energy (things moving and heat).  Light is about the closest anything comes to being pure energy, but it’s not pure energy so much as it’s one of the several kinds of energy that isn’t tied up in matter.  It’s “matterless”, sure, but that doesn’t mean that electromagnetic fields (light) are any closer to being pure than, say, gravity fields (another, very different, massless form of energy).  “Pure” energy: nope.  Some form of energy without matter: that happens.

So, energy can change from one form into another into another into another, etc., but the question remains: what is energy?  The answer to that is a little unsatisfying.

There’s this quantity, that takes a lot of forms (physical movement, electromagnetic fields, being physically high in a gravitational well, chemical potential, etc., etc.).  We can measure each of them, and we know that the total value between all of the various forms stays constant, and just like every other every constant, measurable thing it gets a name; energy.

If fusion in the Sun releases energy*, then the amount released is E = (Δm)c2 (where Δm is the change in mass between the hydrogen input and helium output and c is the speed of light).  If that energy travels from the Sun to the Earth as light, then each photon of that light carries E=hν (Planck’s constant times frequency), of it.  If those photons then fall onto a solar panel, that light energy can be converted into electrical energy.  If that electrical energy runs a motor, then the energy used is E = VIT (voltage times current times time).  If that motor is used to compress a spring, then the energy stored in the spring is E=0.5kA2 (where k is a spring constant, and A is the distance it’s compressed).  If that spring tosses a stone into the air, then at the top of its flight it will have converted all of that energy into gravitational potential, in the amount of E = mgh (mass of the stone times the acceleration of gravity times height).  When it falls back to the ground that energy will become kinetic energy again, E=0.5mv2 (where m is the stone’s mass and v is its velocity).  If that stone falls into water and stirs it up, then the water will heat up by an amount given by E = C(ΔT) (where C is the heat capacity of water, and ΔT is the change in temperature).

The “same energy” is being used at every stage of this example (assuming perfect efficiency).  But there’s no “carry through” that makes it from the beginning to the end.  The only thing that really stays the same is the somewhat artificial constant number that we Humans (or more precisely: Newton) call “energy”.

When you want to explain the heck out of something that’s a little abstract, it’s best to leave it to professional bongo player, and sometimes-physicist Richard Feynman:

“There is a fact, or if you wish, a law governing all natural phenomena that are known to date.  There is no known exception to this law – it is exact so far as we know.  The law is called the conservation of energy.  It states that there is a certain quantity, which we call “energy,” that does not change in the manifold changes that nature undergoes.  That is a most abstract idea, because it is a mathematical principle; it says there is a numerical quantity which does not change when something happens.  It is not a description of a mechanism, or anything concrete; it is a strange fact that when we calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same.  (Something like a bishop on a red square, and after a number of moves – details unknown – it is still on some red square.  It is a law of this nature.)

(…) It is important to realize that in physics today, we have no knowledge of what energy ‘is’.  We do not have a picture that energy comes in little blobs of a definite amount.  It is not that way.  It is an abstract thing in that it does not tell us the mechanism or the reason for the various formulas.” -Dick Feynman

 

The Green Lantern picture is from here.

*Every time energy is released from anything, that thing ends up weighing less. It’s just that outside of nuclear reactions (either fission or fusion) the change is so small that it’s not worth mentioning.

Posted in -- By the Physicist, Physics | 59 Comments

Q: Why is Schrodinger’s cat both dead and alive? Is this not a paradox?

Posted on April 13, 2013 by The Physicist

One of the original questions was: A basic rule of logic is that something cannot contradict itself. It is impossible for P to be true and not true. Doesn’t Schrödinger’s cat violate this law and therefore invalidate logic?

The experiment

Schrödinger proposed this thought-experiment to demonstrate how ridiculous quantum super-position is.  Basically the multiple states of a single atom (decayed and not decayed) causes a cat to be in multiple states (living and dead).

Physicist: The resolution to this comes from a careful look at what is meant by the “state” of something.  Turns out, logic is safe from Lil’ Schrödinger’s claws.

There’s a big difference between “reasonable” and “logical”.  To see the difference, find a calm, reasonable person and talk to them, and then (this is more difficult) find a professional logician and try to talk to them.

Talking to professional Logicians: more effective than water-boarding.

Talking to professional Logicians: among the more frustrating conversations you’ll ever have.

It’s pretty reasonable to say that a single thing must be in one state or another, especially if those states are mutually exclusive.  It’s obvious.  It’s common sense.  In fact, it’s so reasonable/obvious/sensible that disagreeing with it would be a good way of being laughed out of every fancy science salon of the 19th century (or at least the occasional salon with sober members).  Logic, on the other hand, has nothing to do with physical reality (neither does being reasonable for that matter).

Logicians start with a big bucket of postulates and symbols and statements, and then run with them.  None of it needs to be “physically motivated” or even remotely intuitive.

Clearly, this reads

Clearly, this reads “P is possibly true if and only if P is not definitely untrue” and also “P is definitely true if and only if it is not possible for P to not be true”.

The statement that things must be one way or another (specifically, that each state is mutually exclusive of the others), is a whole new logical statement on its own.  The statement even has a name: “counterfactual definiteness“.  Overly-complicated terms like that are just made up so that people will think that physicists are wizards-of-smartness.  A better term for things needing to be in a definite state is “realism”.  While realism is “obviously true”, is isn’t necessarily true (not “logically true”), and point of fact: isn’t true.

There’s a famous no-go theorem in quantum physics called “Bell’s theorem” that says that, given the results of a variety of experiments involving entanglement, “local realism” is impossible.  This means that things always being in single states requires the exchange of some kind of faster-than-light signals.  Or conversely, if no effects can travel faster than light, then things must be allowed to be in multiple states.

It’s pretty natural to jump to the conclusion that things are communicating faster than light.  Losing realism is philosophically, even mathematically, a bitter pill to swallow.  Unfortunately, there are a lot of problems with faster than light stuff (like this one!).

It turns out that the universe doesn’t seem to have any problem dropping realism.  Things are perfectly happy being in multiple states at the same time: particles being in multiple positions or energy states, single events happening at multiple times, or (admittedly reaching a little past our grasp) being in multiple states of living and dead.  The last of course has never been observed in the lab (and probably never will be), but this is a well-studied property otherwise.  We’ve seen multiple-stated-ness in every physical system we’re capable of measuring the effect in.  So far, there doesn’t seem to be any limit to the scale at which quantum weirdness shows up.

In short, it does make sense to say that things must be in a single state or another, but it isn’t necessarily “logical”.  The universe couldn’t care less about what makes sense.

Answer gravy: This bit threatened to derail the flow of the post.

Realism is technically a statement that limits the exact nature of what kind of states are allowed.  For example, only the states |living\rangle and |dead\rangle are allowed.  When the cat is both living and dead it’s technically just in multiple states in certain “measurement bases”.  So the cat could be in the single state \frac{1}{\sqrt{2}}\left(|living\rangle+|dead\rangle\right).

We see this all the time in the polarization of light, for example.  A diagonally polarized photon is in a single state, |\nearrow\rangle.  But, if you insist on looking at it (measuring it) in terms of horizontal and vertical polarizations, then you find that it must be in multiple states, |\nearrow\rangle = \frac{1}{\sqrt{2}}\left(|\rightarrow\rangle + |\uparrow\rangle\right).  This moves the problem from being a purely philosophical/logical problem, to one of defining what is meant in detail by the word “state”.

The answer to whether Schrödinger’s cat is in multiple states becomes a resounding “Yes!  Unless some very specific measurement is set up, in which case: no!”.

Posted in -- By the Physicist, Logic, Physics, Quantum Theory | 48 Comments

Q: What kind of telescope would be needed to see a person on a planet in a different solar system?

Posted on April 8, 2013 by The Physicist

Physicist: When talking about telescopes there are two quantities to take into account; the “light gathering power” and the “resolving power” of the telescope.  “Light gathering power” is just how much light can be collected by the telescope.  “Resolving power” is a measure of the smallest angle that the telescope can reliably detect.

Telephoto lenses

Telephoto lenses need to be large because the amount of light that bounces off of a distant object and that then goes through the lens is fairly small.  Being wide means they can gather more light.  They need to be long for other, more subtle, reasons.

Because light is a wave it has a way of spreading out (technically: diffracting).  The smaller the telescope the more the waveness becomes a problem.  If the angle between two distant points is θ, the light in question has a wavelength of λ, and the size of your telescope is D across, then the smallest resolvable angle is approximately \theta = \frac{\lambda}{D}.

What’s a little weird is that this D isn’t just limited to the size of the mirror or lens of a single telescope.  By cleverly networking telescopes together you can make them act like a single large telescope.

The VLA, or "Very Large Array", was named in honor of Professor Wilhelm Von Verylarge

The VLA, or “Very Large Array”, was named in honor of Professor Deirdre Von Verylarge.  By combining information from all of these radio-telescopes together they behave like one very large telescope that is effectively 36km across (the dishes are mobile and can be separated by at most 36 km).

Coincidentally, something that’s a large distance L away, and that’s a size S across, takes up an angle of approximately \theta=\frac{S}{L}.  So, if you want to be able to see something, you need \frac{S}{L}\ge\frac{\lambda}{D}.

Visible light has a wavelength of about half a micrometer (one two-millionth of a meter), people are about a meter across (assuming a spherical person), and the Earth is about 13,000,000 meters across.  So, using ground-telescopes that are perfectly constructed and networked, we could spot something person-sized from about 1/400th of a light year away, or about double the distance to Pluto.  For comparison, the distance to the nearest star is about 4 light years.  So, using ground based telescopes we can’t come even remotely close to seeing a person standing around on a planet in another solar system.

The nearest known, reasonable, candidates for being an Earth-like planet (as of April 2013) are about 20 light years away (HD 20794 d, Gliese 581 c, and Gliese 667C c).  Spotting dudes and ladies on one of these worlds requires, at minimum, a telescope array that’s at least 100 million km across.  That’s an array more than half the size of Earth’s orbit.  The good news is that an array like that (under absolutely ideal circumstances) isn’t that difficult to create.  Setting aside that the telescopes would each need to be essentially perfect for their size (Hubble-quality), all we’d need to do is set them up in solar orbits about the size of Earth’s orbit.  This is a lot easier than sending them to another planet, and about as hard as sending them to crash on the Moon.

So, assuming that we could set all that up, the problem stops being one of resolving power, and becomes one of light-gathering power.

On a sunny day we’re hit by about 1021 (1,000,000,000,000,000,000,000) photons (give or take) every second.  Assuming that a fair fraction of those escape into space, then that number, which seems large, is all that distant aliens have to work with.  Over 20 light years that scant 1021 photons means you would need a telescope array with an area of more than 500 million square kilometers to catch just one photon per second.  That’s the size of the surface area of Earth.  In the mean time there’s a lot of other light flying around, and single photons are pretty hard to detect so… the signal-to-noise ratio would be small.

Creating an array capable of seeing big stationary things like rivers and mountains on other worlds wouldn’t be too difficult, because you can just use tremendously long exposures to overcome the whole light-gathering issue.  This is a pretty standard trick in astronomy; the Hubble Deep Field took a more than a week of total exposure time.  There would be some issues with the fact that those distant planets are moving and whatnot, but there are clever ways around that too.

People, and probably aliens too, move around a lot.  So if you want to get a picture of one, you need the exposure to take less than, say, a second.  Unless you catch E.T. literally napping.  I would wildly guestimate that you’d need at least a few thousand photons per second to overcome the signal noise enough to say for certain that you’re looking at something real.

So, to answer a somewhat more detailed question; to get a picture of an alien that’s person-sized, standing on a world 20 light years away, so that it takes up one pixel in the image, using an exposure time of about one second, would require an array of telescopes with exposed mirrors and lenses with an area totaling more than several thousand times the Earth’s surface area and spread out over a region about the size of Earth’s orbit.

This isn’t technically impossible, but it would be “expensive”, and would require substantially more materials than are likely to be reasonably found in our solar system.  It probably isn’t worth it to get a blurry, tiny picture of some alien picking it’s nose 20 light years away and 20 years ago.

Of course, if you wanted to see farther, you’d need a much larger telescope array.

Posted in -- By the Physicist, Astronomy, Physics | 16 Comments

Q: Is Murphy’s law real?

Posted on April 1, 2013 by The Physicist

Physicist: The mathematical statement of Murphy’s Law, as used in scientific communities, is tremendously complex.  But the common form, “everything that can go wrong will”, is fairly accurate and more than sufficient for most applications.

The short answer is: yes, Murphy’s Law is real.  There are a lot of basic logical reasons for this.  For example; nothing lasts forever, so eventually every part of every machine will eventually break down.  Or, because being in traffic involves spending more time getting from place to place, you can expect to spend disproportionately more time in traffic than not.  But, as you’ve no doubt noticed, using logic and random chance alone it’s impossible to explain away the preponderance of horrible happenstances that show up seemingly without pause, everywhere, at all times.

“Coincidences” like that are a strong indication that a physical law is in play.  We can clearly see that Murphy’s law is both real, and unfairly applied to people colloquially known as “clumsy”.  Robert Oppenheimer, in addition to some entirely forgettable work he did in physics, pioneered research into Murphy’s law by studying his own unfortunate condition.  Bob’s affliction was first brought to the attention of his colleges when it was noticed that when he was in the lab, everyone’s muffins and buttered scones were 42% more likely to land upside-down.  Even sandwiches with particularly binding peanut-butter were more likely to open on the way down.

(Left) Murphy, the discoverer of "Murphy's Law" shown here after a flossing incident. (Right)

(Left) Wilhelm Murphy, the discoverer of Murphy’s Law, shown here suffering from complications after a gum-chewing incident. (Right) Oppenheimer, extended and modernized our knowledge of Murphy’s Law.  This is the only known picture of Oppenheimer with his eyes open.

Oppenheimer, after he was politely asked not to work in the laboratories, made several starling discoveries such as the fact that Murphy’s Law is “recursive”, “pessimistically optimal”, and “robustly unfair”.  The recursive nature of the Law is one of the more obvious.  It says, in effect, that Murphy’s Law can’t be out-smarted.  For example, washing you car is almost certain to make it rain. However if your intention is to make rain, then washing your car will probably just make someone slip and fall.

Oppenheimer was involved in one of the better examples of Murphy Recursion.  During a celebration of his accomplishments and “clumsiness”, some of his fellow scientists constructed a lever attached to a prop chandelier, such that when Oppenheimer walked in and inevitably pulled the lever the chandelier would drop.  However, they forgot to take into account the recursive nature of Murphy’s Law, and the lever didn’t work.  Of course, had they tried to take Murphy Recursion into account, something else would have gone wrong.

Many people known to be “unlucky” or “followed by a black cloud of misfortune” are the sad victims of the fact that Murphy’s Law is demonstrably unfair.  This is the essential reason behind why computer problems only exist until you try to show someone else.  The range of “what can go wrong” varies wildly from person to person.  For Roy Sullivan (for example) being struck by lightning is something that can go wrong (and did go wrong seven times).  Despite specifically trying to avoid storms and clouds, he could barely leave his house without some lightning bolt setting him on fire.

So, Murphy’s Law is certainly very real, and can even be measured qualitatively.  However, it can’t be anticipated or taken into account.  We can only wait for terrible, unfortunate things to happen, and hope that they won’t be too bad.

Posted in -- By the Physicist, April Fools | 38 Comments