Physicist: Mostly awesome. Eventually.
Recently, some of the folk at Google claimed to have achieved “quantum supremacy” (here’s what they had to say about it). Google has, like many other big companies and nations, been very gung-ho about research into quantum computers, and that research has been coming along remarkably fast in spite of stupefying engineering hurdles in the way.
Quantum computers aren’t “better computers”. They’re a completely new way to do computations that’s practically unrecognizable to “classical” computer science. Saying that a quantum computer is better than a classical computer is a little like saying that a bicycle is better than a horse; there are comparisons to be made, but “better” isn’t a particularly useful way to frame them.

Like quantum and classical computers, the best option is typically some combination of both.
For example, if you want to factor big numbers (to break RSA based cryptosystems, for example) or search an unsorted database, then quantum computers promise speeds that are impossible for a classical computer. On the other hand, if you’d like to add two numbers together or look at pictures of horse-bikes, a classical computer is arguably better (inasmuch as it is hundreds of millions of dollars cheaper).
Quantum supremacy is a historical milestone more than anything, when a quantum computer manages to do a calculation that no classical computer is likely to ever match. A few weeks ago, Google’s “Sycamore” computer did just that. But your bank accounts are safe. Sycamore isn’t nearly powerful enough to break crypto keys and the calculation it did is arguably… a little pointless.
Sycamore was given a series of random quantum circuits to simulate, which it was able to do. Barely. According to Google, “Our largest random quantum circuits have 53 qubits, 1113 single-qubit gates, 430 two-qubit gates, and a measurement on each qubit, for which we predict a total fidelity of 0.2%.” That 0.2% isn’t how often it fails, that’s how often it works. We’re not launching boldly into the era of quantum supremacy so much as we’re limping across the starting line. Baby steps.
Even so, in just a few minutes Sycamore did the same calculation 5 million times and, since mistakes are random and not-mistakes are consistent, that 0.2% is good enough to be useful. The most powerful supercomputers could do the same calculation once in about ten thousand years (brags Google).
Simulating random quantum circuits using a quantum computer might seem silly, but only because it is. This is the sort of thing that you might do if you needed to prove to someone else that you really do have a quantum computer, but Google already knows that. Because they built it. Their test boils down to asking Sycamore “Are you really a quantum computer?” to which Sycamore responded “…yes. Wait, didn’t you build me?”. We can believe the answer because it would take thousands of years for a classical computer to lie.
It’s worth stepping back to consider what a computer is and what makes quantum computation so alien. In a moment you’re going to get the overwhelming urge to yell “n’ doy!”, but bear with me.
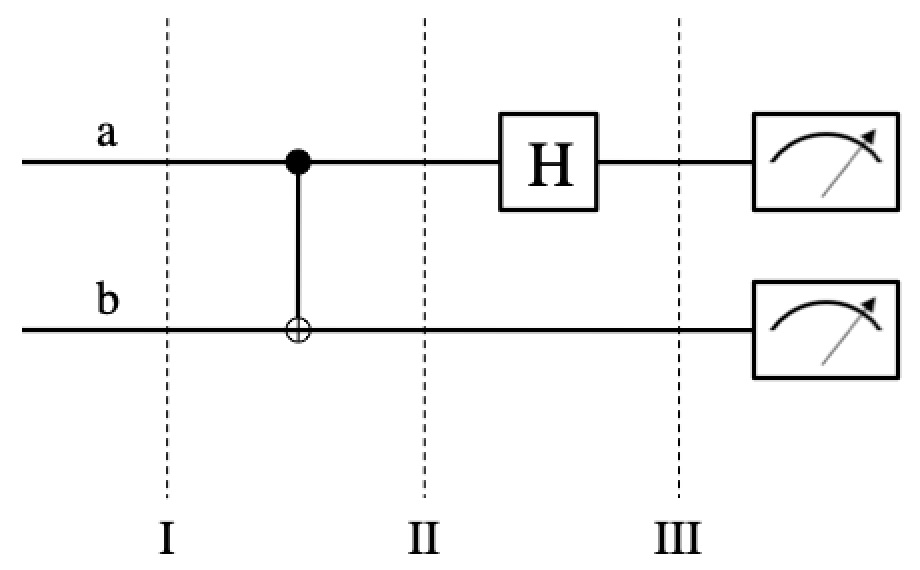
A computer takes information as input, does something with it, and spits out a result. What kind of information, how it does what it does, and what the output looks like, all depend on the “architecture” of the computer. For classical computers (like whatever you’re using right now), information takes the form of a heck of a lot of bits and logic gates that compare those bits and produce new bits. “Bits” are “binary digits” and each describes some binary choice: 0/1, on/off, trek/wars, up/down, etc. Logic gates are the simplest, smallest part of a computer, manipulating bits one or two at a time. For example, the “and gate” does this: 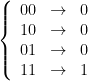
There are a lot of ways to do this. Today we use transistors, because they’re efficient, fast, and we’ve gotten weirdly good at making them tiny. In (NPN type) transistors, current is only allowed to flow across when a secondary voltage pushes electrons into the “conductive band”, so they’re available to carry electricity. That’s an “and gate” right there: unless two voltages are applied, one to make the transistor conductive, and another to actually push current across it, no electricity passes through. Before transistors phased every other contender out, “relays” were a common way to construct logic gates: current from one source generated a magnetic field that physically grabbed a metal plate and pulled on it to close a switch, so that another current has the opportunity to flow (which is really brute-force logic). Although they could be loud enough drive nearby engineers crazy, at least they didn’t wear out all the time or set things on fire the way vacuum tubes did. For some sense of what relays sound like, watch an old Star Trek. Somebody at Paramount guessed super wrong about the future (of computers and hair styles at least).

All three of these things serve the same basic function, just in different ways. Left: In vacuum tubes, an excess of charge on a screen (the black thing) prevents electricity from literally making the jump between a cathode and anode (the plates above and below it). Middle: In relays, current flows through a solenoid (the coil of wire) generating a magnetic field that physically pulls a switch shut or open, controlling current through a second wire. Right: In transistors, a tiny voltage provides either electrons or “holes” (a lack of electrons) to carry electrical current across a semi-conductor.
The big things that make quantum computers different are superposition, qubits, and quantum parallelism (which are kinda three sides of the same coin). Bits are either one of two states (0 or 1). Qubits, “quantum bits”, are any combination of two states. That means that even a single qubit is already much more complicated than a single bit.
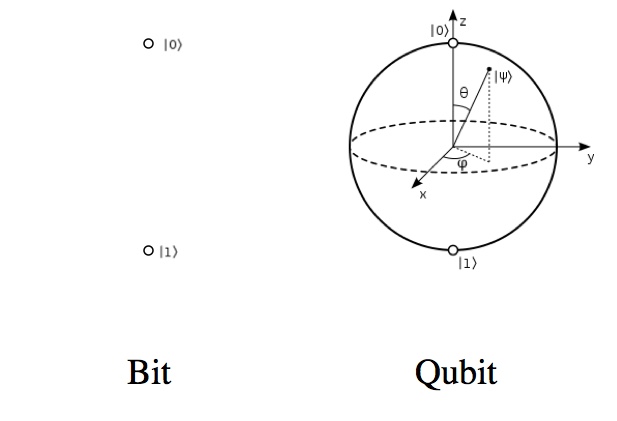
One bit is as complicated as “this or that”. One qubit is as complicated as the surface of a “Bloch sphere”: this or that, and everything in between, and also every “complex valued” combination.
In order to simulate a single qubit, a classical computer needs to keep track of two complex numbers to fair accuracy (depending on how accurate the simulation needs to be). But that’s not what makes simulating quantum computers hard; it’s quantum parallelism.
If you’ve heard of “entanglement”, then you’ve probably heard it described as “two particles spookily connected to one another”, which makes it sound like entanglement is about sending signals. But at it’s heart, entanglement is about something a bit more profound. You can’t describe a quantum system by looking at one part at a time, you have to consider all of it together. Two entangled particles share a single state between them.
A single tiny thing can be in a superposition of states. If there are only two states, like with an electron’s spin, then you’ve got a qubit and you can describe the superposition of up and down states like this: 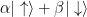 . Physicists like to use Greek letters for complex numbers because it makes their math look fancy. But if you have, say, three electrons, then your three qubits are more than three times as complicated. If the three electrons are “separable” (which means they’re not entangled and they can be accurately considered one at a time), then their collective state looks like this:
. Physicists like to use Greek letters for complex numbers because it makes their math look fancy. But if you have, say, three electrons, then your three qubits are more than three times as complicated. If the three electrons are “separable” (which means they’re not entangled and they can be accurately considered one at a time), then their collective state looks like this:
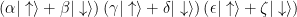
That’s all three electrons in their own superpositions. However, if those electrons have been brought together and had a chance to interact, affect each other, and become entangled (which is a typical situation), then their collective state looks like this:

For three qubits this isn’t much of a jump, from  terms to
terms to  , but that exponent makes a big difference. 100 bits takes, well, 100 bits to describe. 100 qubits takes
, but that exponent makes a big difference. 100 bits takes, well, 100 bits to describe. 100 qubits takes 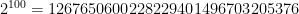 complex numbers to describe. That’s a huge amount of information for even modest a quantum computer to work with.
complex numbers to describe. That’s a huge amount of information for even modest a quantum computer to work with.
Hemoglobin uses around 10,000 atoms to do two things: grab oxygen and let go of oxygen. Presumably, if it could be done better with fewer atoms, we wouldn’t have hemoglobin, so understanding how all of this mess works together is important.
The same phenomena that makes quantum computation exponentially complex also makes quantum systems exponentially difficult to simulate. For example, we can simulate a handful of atoms without too much trouble, but what we’d really like to do is simulate entire proteins, so we can get a better handle on (and maybe monetize?) the nature of life itself at the most basic level. The problem is that proteins generally have many thousands of atoms, and its collective behavior (like any quantum system) is exponentially more complicated than the sum of its parts. So this is a great opportunity for quantum computers to step in and do the thing they do best: act quantum. Simulating proteins, drug interactions, and really anything involving lots of atoms, may be the killer app for quantum computers. If and when they get off the ground, this may be the big thing we notice (unless, for some reason, I can’t predict the future).
And yet, quantum computers are not usually exponentially more powerful or faster than classical computers. They don’t actually “check every possibility” when they do a calculation. If they did, we could ask incredibly broad questions with very specific answers (“what is best in life?“) and then use some protocol to sort them out. What’s happening inside a quantum computer is more akin to wave interference, where waves from different sources overlap and interfere to create some combined pattern that isn’t the result of any one source in particular. The output is always the combined result of every input. The trick is in getting the answers you don’t want to cancel each other out and the answers you do want to add together. If that sounds difficult and frustrating: yes. Again, they’re not “better” than classical computers, but so wildly different that they open up new options.
There’s also a pretty spectacular bottle neck between what a quantum computer can think and what it can say. For example, when you measure an electron’s spin, it’s either up or down regardless of whatever else is going on. This is true in general: while N qubits can be in  states together, when you get around to measuring them, each will only produce a single bit for N bits total (this is an application of Holevo’s Bound). With 300 qubits, a quantum computer would have access to more states than there are atoms in the visible universe, and yet its output would be shorter than this sentence.
states together, when you get around to measuring them, each will only produce a single bit for N bits total (this is an application of Holevo’s Bound). With 300 qubits, a quantum computer would have access to more states than there are atoms in the visible universe, and yet its output would be shorter than this sentence.
The big worry with quantum computers is an end to the age of encryption, which would be bad for anyone who wants more privacy than instagram nudists. We (the people) have two big things going for us. First, the Shor algorithm requires at least twice as many qubits (realistically, a hell of a lot more to handle error correction) and while the best quantum computers today only several dozen qubits, a good RSA key is hundreds or thousands of bits long. So there’s some time. Second, RSA is not the only kind of encryption. Governments and companies around the world are already making the move to “post quantum cryptography“. Even without functioning quantum computers, quantum technology gives us access to “quantum cryptography” which is basically a method for creating perfectly random numbers (which professional cryptographers love) at two locations without actually sending those numbers, as well as determining whether someone is listening in (which paranoid cryptographers love).