The original question was: Is this f’real?
Astronomer: The Alcubierre spacetime metric is named after a Miguel Alcubierre, a physicist who was also a Star Trek fan. It describes a type of bubble in space, where you could put, for example, a spaceship named USS Enterprise. Within the bubble space is isn’t doing anything weird, but in front of the bubble you scrunch up space and behind the bubble you stretch it out. If you could create space that was warped in this particular way, you could sit in your spaceship inside the bubble and move space around you faster than light in a way that would make it seem like you’d traveled at speeds faster than light. In reality, only the space itself would have travelled faster than light, which doesn’t break the speed limit rules imposed by relativity.

Bend some space like this and you can head for the second star to the right, and go straight on till morning!
The Alcubierre metric is a real solution to Einstein’s equations, which describe the ways in which space is allowed to bend or warp. There is no theoretical reason to think space couldn’t bend in this way, except for one very major problem. In the equations that describe the Alcubierre metric, one of the mass terms has to be negative for things to work out.
Know where I can get some negative mass? Didn’t think so. Negative mass, which is fundamentally different than anti-matter, would experience gravity as a repulsive force. Too bad nobody has ever discovered any negative mass floating around out there or made any substantial amount it. You can make really tiny amounts of negative mass/energy for very short periods of time in the lab, by “borrowing energy from the uncertainty principle,” but it’s not clear this could be scaled up to the macroscopic level like it would need to be to create a useful warp bubble.
It’s probably best negative mass doesn’t exist, because it’s incredibly creepy! For example, imagine you had a chunk of normal mass and a chunk of negative mass in space. The negative mass would fall towards the regular mass, but at the same time create “repulsive gravity” which would then push the normal mass away. Lather, rinse, repeat, and you could theoretically accelerate those two chunks off into the stars forever. This smells suspiciously like perpetual motion, and would break the well established principle of conservation of energy. Given that, it’s understandable that we’re not packing the SPF 5000 for our super fast trip to Alpha Centauri Bb.
Physicist: It is for real, but don’t go reserving flights. There has been some theoretical research into Warp drives for about 20 years starting, not surprisingly, within months of the end of TNG. Back in the day Einstein figured out how mass/energy and the curvature of spacetime relate to each other with the narcissistically named “Einstein field equations“. These equations tell you how spacetime will be stretched and curved in the presence of a distribution of matter (for example, put a bunch of matter in one place, and spacetime will “pucker” in such a way that we get gravity). But these equations can be turned on their head; if you want spacetime twisted up in a particular way, you can find out how matter and energy need to be arranged to make that happen.
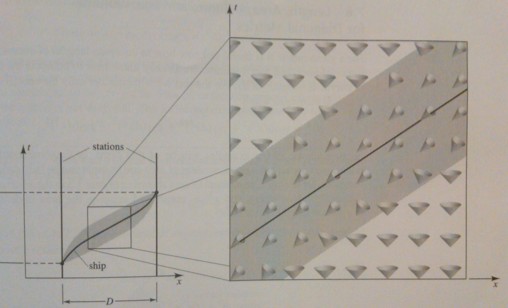
By bending spacetime in a particular way you can make it so that locally you move slower than light, but that the overall effect is faster-than-light travel. The arrangement of matter and energy that allows for this is unfortunately impossible. This diagram is from page 145 of “Gravity”, by Hartle.
Warp drive research always hinges on the idea that we should be able to arbitrarily manipulate stunning amounts of energy, and moreover, that a hell of a lot of that energy can be negative (essentially, “magical freeze-ray” powered warp drives). To date, we haven’t been able to isolate negative energy independent of a burst of positive energy (in any form), and there have been a few arguments (not proofs) that there may be an uncertainty-principle sort of thing that forces this to always be the case. Negative energy and matter carry with them an amazing array of fundamental issues. For example, if you bring matter and anti-matter together you get a big boom, resulting in a big increase in entropy (as light and new particles fly in every direction), but if you bring matter and negative-matter together they just quietly blink out, resulting in a big decrease in entropy (which is a thermodynamic no-no).
But! Assuming that negative energy can be harvested (even in theory), and very carefully controlled and manipulated in spectacular ways, and if a number of very fundamental theoretical issues can be ironed out, then this is totally a way to travel faster than light in a very Star Trek kind of way (as opposed to a BSG “jump drive“). Warp drives have been in the news a bit recently because it was shown that there are “spacetime geometries” that require less of the very-probably-impossible negative-matter than was originally thought (presumably, also because warp drives are awesome). This is a little akin to saying “my unicorn powered wish-making machine is now more feasible, because the unicorns can be any color, not just blue”.
For most physicists the Alcubierre drive is a cute tool for teaching general relativity, but in application smells a lot more like perpetual motion and anti-gravity machines than a device we’re ever likely to see.
There are some hopeful legit physicists, but not many.