Q: How does the Oberth Effect work, and where does the extra energy come from? Why is it better for a rocket to fire at the lowest point in its orbit?

Posted on January 19, 2013 by The Physicist

Physicist: When a rocket fires it increases its speed by some fixed amount called the “ΔV” (delta V).  If the original speed is W, and the rocket speeds up by ΔV, then the change in energy is: \frac{1}{2}M(W+\Delta V)^2 - \frac{1}{2}MW^2 = \frac{1}{2}M(\Delta V)^2 + MW\Delta V.  So here’s the problem; notice that the increase is not just \frac{1}{2}M(\Delta V)^2, but is instead bigger when the initial velocity is bigger.  Isn’t that weird?

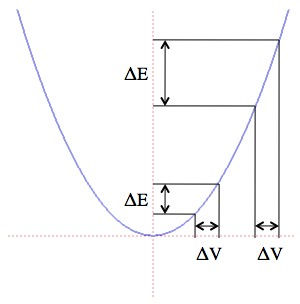
The change in energy is greater for the same change in speed for different starting speeds.

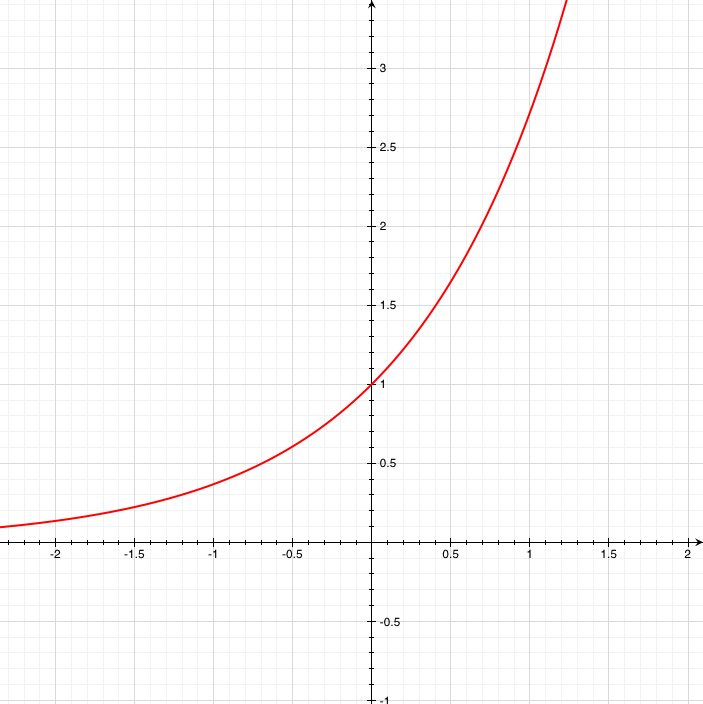
Kinetic energy vs. Speed: The change in energy is different for different starting speeds even if the change in speed is the same.

This comes up a lot when you’re shooting rockets around the solar system.  If the rocket has a big elliptical orbit, then it’ll be moving quickly at the closest part of the orbit and slowly at the highest part of its orbit (just to be confusing, these points are called the “periapsis” and “apoapsis”).  So, very weirdly, if the rocket fires when it’s moving the fastest it’ll pick up more more kinetic energy and it’ll be able to get higher and farther.  But if the rocket fires when it’s moving slowly it gains less energy, and at the most extreme, if W = -ΔV/2, then the energy doesn’t change at all (the rocket just switches direction).  This is a basic rule of thumb in rocket science; if you’re going to fire your rocket, fire it at the lowest point in its orbit.  But the question remains: Wha…?  Why?

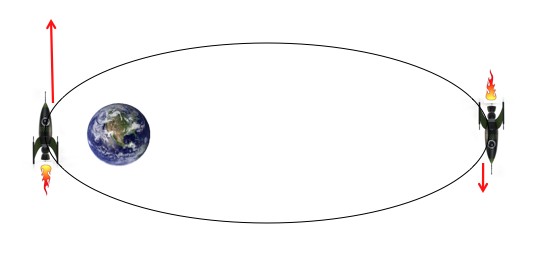
Krakow! Krakow! Two direct hits!

At different parts of an orbit the same amount of fuel translates into different amounts of kinetic energy.  This “Oberth effect” comes about because the ship travels at different speeds at different points in the orbit.

The very short answer is that you need to take into account what the exhaust is doing as well as what the rocket is doing.  We usually think of a rocket as a thing that propels itself through space.  In fact, it’s better to think of a rocket as a “gas cannon” that throws as much stuff as possible, as fast as possible, out of its more interesting end.

"boring end" = "safe end"

Rockets and cannons both throw stuff as fast as they can. The only real difference is that a cannon is nailed down.

When the rocket is slow the exhaust travels quickly and carries away a lot of kinetic energy.  When the rocket is fast the exhaust is closer to sitting still (in fact, if the rocket is already traveling at the exhaust velocity, the exhaust is basically dropped off).  Overall, energy is always conserved (it’s practically a law), it’s just a question of how much goes into the rocket, where it’s useful, and how much goes into the exhaust, where it’s not.

So check it!  Imagine that a parcel of fuel with mass m gets burned and ejected at a speed of ΔU.  Conservation of momentum says that the momentum of the rocket and fuel before burning is the same as the momentum afterward.  Mathematically, this is MΔV + mΔU = 0.  The energy before the burn is E = \frac{1}{2}(M+m)W^2 and the energy afterward, from the rocket and the fuel parcel, is E = \frac{1}{2}M(W+\Delta V)^2+\frac{1}{2}m(W+\Delta U)^2.  The change in energy is

\begin{array}{ll} \frac{1}{2}M(W+\Delta V)^2+\frac{1}{2}m(W+\Delta U)^2 - \frac{1}{2}(M+m)W^2\\ =\frac{1}{2}MW^2+MW\Delta V+\frac{1}{2}M(\Delta V)^2+\frac{1}{2}mW^2+mW\Delta U+\frac{1}{2}m(\Delta U)^2 - \frac{1}{2}(M+m)W^2\\ =MW\Delta V+\frac{1}{2}M(\Delta V)^2+mW\Delta U+\frac{1}{2}m(\Delta U)^2\\ =MW\Delta V+\frac{1}{2}M(\Delta V)^2+mW\left(-\frac{M}{m}\Delta V\right)+\frac{1}{2}m(\Delta U)^2\\ =MW\Delta V+\frac{1}{2}M(\Delta V)^2-MW\Delta V+\frac{1}{2}m(\Delta U)^2\\ =\frac{1}{2}M(\Delta V)^2+\frac{1}{2}m(\Delta U)^2\end{array}

Huzzah!  This is exactly what you’d expect; when you take into account all of the stuff that’s flying around, all of the weirdnesses disappear.  The dependence on the initial speed is gone, and you’re left with the same gain in energy you’d see from a rocket starting from a stand-still.  So the Oberth effect, which seems like a violation of the conservation of energy at different speeds, is just a failure to take into account that a rocket slings fuel.  Rather than being a magical extra boost when a rocket is traveling fast, it’s just a cute and fortunate distribution of energy.

Posted in -- By the Physicist, Physics | 27 Comments

Q: How do lenses that concentrate light not violate the second law of thermodynamics? If you use a magnifying glass to burn ants, aren’t you making a point hotter than the ambient temperature without losing energy?

Posted on January 13, 2013 by The Physicist

Physicist: This is a surprisingly subtle question.

It certainly impossible to create new energy, but there’s nothing to stop you from piping energy from one place to another (say, by running hot water from a boiler to somewhere else).  The case of sunlight and a lens is just a matter of controlling where the energy is going in a slightly more abstract way.  Focusing light from the Sun doesn’t decrease entropy, because what a lens does (this is a little hand-wavy) is to exchange “direction information” for “position information”.  The light from one direction (from the direction of the Sun) gets brought together in one position (the focus).

Parallel light

Perfectly parallel light can be focused at a point, but light from different directions focus at different points.  Light from multiple directions can’t be focused to one point.

So, if the light from the Sun weren’t so parallel we wouldn’t be able to use a lens to focus it so well.  This is why, on a cloudy day, you can’t burn things with a magnifying lens, even when it’s fairly bright outside.  The energy is still there, it’s just scattered.

A little surprisingly, focusing parallel light to a point does not change the entropy of the light, and there’s a cute way to show that.  A good rule of thumb for entropy is, “if you can reverse it, then the entropy is constant”.  In this case, were you so inclined, you could put a second lens after the first that “re-parallelizes” the light.

The act of focusing light is reversible, so it doesn't increase entropy.

The act of focusing parallel light is reversible (here’s how), so it doesn’t increase entropy.

It seems as though there should be some way to bring together lots of light beams using lenses and mirrors and… optical cables or something, that would allow you to get a tiny region as hot as you want.  But as it happens: no.  This is yet another example of the universe having an obnoxious no-go law.

There is a general thermodynamic rule which says that you can never focus energy in such a way that the target is hotter than the source.  So, no matter how many mirrors and lenses you have, you can never focus sunlight in such a way that it’ll be hotter than 5800K (the surface temperature of the Sun), but you can get close.  In practice that isn’t too useful, because machines tend to break at surface-of-the-sun temperatures.

If you were in the bright

If you were in the bright spot you’d see a bigger image of the Sun through the lens.  With more directions that end in a hot source, the focal point gets hotter.

A good way to think about this is to imagine yourself meandering about in the surface of the Sun, and then imagine yourself lounging at the focus.  If you were in the upper layers of the Sun, you’d notice that in every direction you look there’s material radiating at around 5800 Kelvin.  As a result, you’d find yourself equilibrating to that same temperature (and burned up real good).  If you were at the focus of an elaborate set up of mirrors and whatnot, then you’d be in the same situation, with every direction you look ending with the Sun.  And the result is the same.

It feels like there should be some way to cheat, but there just isn’t.  If you could find a way to get your target hotter than the source, then you’d have yourself a genuine over-unity device!

The magnifying glass picture is from here.

Posted in -- By the Physicist, Entropy/Information, Physics | 55 Comments

Q: What makes natural logarithms natural? What’s so special about the number e?

Posted on January 7, 2013 by The Physicist

Physicist: “e” shows up on its own a lot, and the frequent appearance of the natural log, “ln“, follows from that.  Almost all of the uses and importance of e and ln are from results in calculus, but those results are so far reaching that they’ve become the standard and have worked their way into everything.  If you’re in pre-calculus, or economics, or some other course that may not involve calculus directly, then chances are that you could just as easily be using log10 or log2 instead of ln and it wouldn’t make much difference (as long as you’re consistent).  Without calculus they’re not particularly special.  However, when you start using derivatives and integrals (calculus) you find that e and the natural log are indispensable and surprisingly natural.

The derivative is an operation that takes a function, f, and spits out a new function, f^\prime, that tells you what the slope of f is.  ex has the remarkable property that the derivative doesn’t change it, so at every point on its graph the value of ex is also the slope of ex at that point.

Y=e^xAt every point on this curve the slope

Y=ex: At every point on this curve the slope is equal to the height.  For example, at x=0, the height is 1 and the slope is 1 (45°).

While it may seem strange to study an operation in terms of what it doesn’t affect, this idea is the backbone of a lot of mathematics.  Fixed points are tremendously important for things like chaos theory and a lot of computer algorithms, and eigenvalues and eigenspaces are about the only way to do linear algebra (which, again, is freaking everywhere).

The other stunningly important property (actually tied up with the calculus property), is that e shows up in Euler’s equation, e^{ix}=cos(x)+i\,sin(x).  This property makes complex numbers useful, and leads into Fourier analysis, which is also in damn near everything.

What follows is mostly calculus.

The three most important properties of e that make it show up all the time are

1) e = \lim_{n\to\infty} (1+\frac{1}{n})^n and e^x = \lim_{n\to\infty} (1+\frac{x}{n})^n

2) e^x is the derivative of itself

3) e^{ix} = cos(x) + i\,sin(x)

#1 shows up every now and then.  For example, the probability of something happening at least once in N tries, if it has a probability of 1/N of happening each time, is 1-(1-1/N)^N\approx 1-\frac{1}{e}.  Also, you can use it to find the actual value of e: e = 1+\frac{1}{2}+\frac{1}{6}+\cdots=2.71828182846\cdots.  But generally #2 and #3 are a lot more important.

Technically, these are all the same property, and that property is that ex can be expressed in a very particular way:

e^x=1+x+\frac{1}{2}x^2 + \frac{1}{2\cdot 3}x^3 + \frac{1}{2\cdot 3\cdot 4}x^4 + \frac{1}{2\cdot 3\cdot 4 \cdot 5}x^5 + \cdots

Notice that if you differentiate this using the power rule, then every term ratchets down and you end up with exactly the same thing.  For example, \frac{d}{dx}\left[\frac{1}{2\cdot 3}x^3\right]=\frac{3}{2\cdot 3}x^2=\frac{1}{2}x^2.

Using this “self-derivative” property of e^x you can show that \frac{d}{dx}\left[A^x\right]=\frac{d}{dx}\left[e^{ln(A)x}\right] = ln(A)e^{ln(A)x} = ln(A)A^x.  So, when A\ne e you get a weird extra ln(A) floating around.

You can also find the derivative of ln(x):

Y=ln(x) \Rightarrow e^Y = x\Rightarrow \frac{d}{dx}\left[e^Y\right] = \frac{d}{dx}\left[x\right]\Rightarrow e^Y Y^\prime = 1\Rightarrow Y^\prime = e^{-Y}\Rightarrow Y^\prime = \frac{1}{x}.

But this means that the anti-derivative of 1/x is ln(x) (which is good to know) and not some other less natural logarithm.  So, anytime you want to find the integral of 1 over some polynomial you’re going to see lots of natural logs.

There are more examples of e’s and ln’s showing up in calculus than there are mathematicians to express them, but long story short; what is tremendously useful in “higher” math trickles down to making an arbitrary choice in “lower” math.

Posted in -- By the Physicist, Math | 10 Comments

Q: If the world were to stop spinning, would the people and everything on it be considered ‘lighter’ or ‘heavier’? Would any change take place? And does centrifugal force have an effect on gravity?

Posted on January 2, 2013 by The Physicist

Physicist: Centrifugal force* due to the spinning of the Earth is certainly a measurable effect, but it’s a small effect.  While the spinning of the Earth doesn’t directly affect gravity, it does off-set it a little.  At the north and south poles objects weigh exactly what they should, and at the equator things weigh slightly less.

Assuming that the Earth is round (which is a pretty good assumption), with a back of the envelope calculation you can figure out the centrifugal force trying to fling you into space.  At the equator (where it’s strongest) that force is approximately 0.35% as strong as Earth’s gravity (0.0035 g’s).  So, if you weigh 300 pounds in Ecuador you’ll find that you weigh almost 301 pounds at the Amundsen-Scott South Pole Station.  0.35% doesn’t seem like much, but it would have a profound affect on at least a few historical events.

Centrifugal force always points out from the Earth’s axis, whereas gravity always points toward the Earth’s center.  So you’d think that somewhere between the poles, where the centrifugal force is zero, and the equator, where it points straight up, that there would be a place where it points a bit sideways.

The farther you are from the Earth’s axis the more centrifugal force you’ll experience. At a latitude of ±45° it pulls sideways more than anywhere else.

Turns out, that place is at 45° north and south latitudes where you “should” find that things get pulled sideways with a strength of half of the maximum: 0.17% g’s.  If the Earth was perfectly round, then this would be exactly the case, and everything in Europe would have to be built slightly tilted (if you’re wondering, the Tower of Pisa would be leaning the wrong way).  However, fluids (and the ground is basically a fluid) move so that the net force always points directly into their surface.

A spinning trough of water. Gravity points down and is constant, while the centrifugal force points out and increases with distance. The surface of the water is always perpendicular to the combined force.

By being distorted a little (an extra 20 km at the equator) the combined gravitational/centrifugal force always points straight up and down.  So, if the Earth were to stop spinning right now then we’d find that buildings were tilted very slightly, things at the equator would suddenly weigh 0.35% more, and eventually the Earth would settle into a more perfectly spherical shape.

Now, if the Earth were to literally come to a sudden and abrupt stop: that would be lots of bad. Things at the poles would be fine, but the closer to the equator the greater the change in speed.  At the equator everyone and everything would suddenly find themselves moving east at mach 1.4 (1,038 mph), and every land mass near the equator would be thoroughly scrubbed by the oceans washing over them.  The economy would take a real hit if the Earth suddenly came to a stop.

*Any time that centrifugal forces are mentioned in the vast crucible that is the internet, a small but vocal cadre makes it known that the centrifugal force isn’t really a force.  Be cool.

Posted in -- By the Physicist, Physics | 72 Comments

Q: Two entangled particles approach a black hole, one falls in and the other escapes. Do they remain entangled? What about after the black hole evaporates?

Posted on December 28, 2012 by The Physicist

Physicist: If all you had access to was the remaining particle, you’d never know the difference.

The way entanglement is often described in popular media makes it sound like voodoo; there’s some kind of magical connection between two or more particles, and doing something to one instantly affects the other. From this point of view it might seem as though you could learn something about the inside of black holes by dropping entangled particles into them, or maybe the outside particle would start acting black-hole-ish.

In practice (reality), entangled particles don’t have any kind of connection with each other, they’re just correlated in a funny way.  In quantum physics things can be in multiple states, such as being in multiple places or multiple energy levels.  This is called a “superposition“.  In classical physics things can only be in one state (I can’t tell you where my keys are, but they’re definitely not in more than one place).

So, say I’ve got some paper bags and one red and one blue marble.  Classically, the marble is either red or blue, but not both.  In quantum mechanics you could prepare a state that’s a superposition of red and blue.

Top: the marble is definitely either red or blue.
Bottom: the marble can be in a superposition of red and blue.

Oddly enough, you can’t describe the world by describing the state of each particle individually.  You have to include states that involve multiple particles that are in multiple states.  Bringing a second bag into the picture, and putting one of the two marbles into each, we find that there are two possible states: red/blue and blue/red.  In quantum mechanics, there’s no problem having a combination of these two states as well.  Notice that since there’s only one marble of each color, the bags are correlated; if you know what’s in one, then you know what’s in the other.

Top: if one bag has a red marble, the other has a blue and vice versa.
Bottom: if one bag has a red marble, the other has a blue and vice versa. However, both bags have both red and blue. In the same way that a single particle can be in multiple states, the bags together are in the states “red/blue” and “blue/red”.

There’s more detail about what exactly entanglement is and how it behaves here, but suffice it to say, when things are correlated and in a superposition of states they’re entangled.  So finally, with that background we can take a look at what happens when you destroy or just take away half of an entangled pair.

A black hole, in addition to all of its other weird properties, does a really good job doing exactly that.  For all practical (experimental) purposes, dropping a particle into a black hole destroys it plenty.  By watching the black hole afterward, it would be impossible to recover information about the one particle you dropped in.  So, what you’re left with is a single particle that’s still in a superposition of states.

Destroying or sufficiently scrambling half of an entangled pair leaves a single particle in a not-entangled superposition.

This, by the way, is what you have even if you don’t destroy the other particle.  Without access to both halfs of an entangled pair, there’s no way to determine if they’re entangled at all.

There was a big debate between some of physic’s heavyweights over whether or not things that fall into black holes are genuinely destroyed, including all of their information, or if information is somehow preserved.  After a few decades of debate, the consensus today is: no, information is conserved.  This has lead to some new ideas like black hole entropy, Hawking radiation, holography theory, and black hole computation (this last one is a little more far-fetched than the others).  In theory, if you somehow managed to keep track of absolutely every detail of everything that fell into the black hole, and then managed to collect most of the Hawking radiation produced by the black hole over its entire life time (which is much, much greater than the age of the universe), then you could in theory have a pretty good chance of correctly guessing which “marble” fell in.

But, for all intents and purposes, if you have an entangled pair of particles and you drop one into a black hole, you’ll be left with one particle that is still technically entangled to the other, but it doesn’t matter.  It’ll behave like any other particle.

Answer gravy: There are buckets more to be said about breaking entanglement, and the statistics of entangled pairs (and halfs of entangled pairs), including the exact nature of the superposition of the remaining particle.  Way too many buckets to fit into one article.  However!  There’s a great resource that goes into ludicrous detail here.  The stuff relevant to this post is in chapter 4.

Posted in -- By the Physicist, Physics, Quantum Theory | 19 Comments

Q: If there are 10 dimensions, then why don’t we notice them?

Posted on December 23, 2012 by The Physicist

Physicist: A “dimension” is a direction.  So, we’re in “3 dimensions” because there are only 3 directions, and every other direction is just a combination of those 3 (and their negatives).  For example, by telling someone how far north, east, and up to go you can direct them anywhere on Earth.  Time is also considered to be a dimension, but there are some subtleties involved with that.

When string theorists talk about space having 10 dimensions they’re talking about all but four of those being “tiny loop dimensions”.  We’re used to thinking of a direction/dimension as extending outward forever, but these tiny directions just make a short loop and bring you back to where you started.

A loop dimension is a direction that repeats.  Sorta like this.

For example, if the universe had two normal dimensions, and the third dimension was a “1-meter loop dimension” then you could move, say, north/south and up/down no problem, but if you looked east or west you’d see the back of your head a meter away.  But unlike a mirror, you could physically poke the back of your head.  Or give yourself a haircut, because why not.

The smaller dimensions are like that, but loop on a distance that is much, much smaller than the smallest particle.  As a result, it doesn’t really make sense to talk about movement in these tiny dimensions, basically because there’s no place to go.

If you restrict one dimension enough, then it can be effectively ignored.  If you’re as big as the alley then you can’t move left-right, but you can still move forward-backward and up-down.

So, if you want to avoid being hit by something, you just step to the side (in any of our 3 dimensions).  You have the option because you have the room.  In the loop dimensions there isn’t enough room, so as far as we (and even particles) are concerned, they may as well not be there.

String theory (which is where all this “10 dimension” talk is coming from) is the only theory of everything on the table today, but unfortunately it hasn’t made any verifiable predictions (yet).  The extra, but undetectable, dimensions are just one example of that.

The portal picture is from here, and the alleyway photo is from here.

Posted in -- By the Physicist, Physics | 21 Comments