Q: Will the world end tomorrow?

Posted on December 20, 2012 by The Physicist

Physicist: Probably not.  Update to follow.

Update (12/22/12): Nope.

Posted in -- By the Physicist, Skepticism | 5 Comments

Q: In an infinite universe, does everything that’s possible have to happen somewhere?

Posted on December 18, 2012 by The Physicist

The original question was: Lets say that we determine that an event is physically possible. So that means the probability of that event is greater than zero. Right? So my question is this. Is there any sense in saying that the event will NEVER happen even if it has a non-zero probability? In other words, if it can happen, will it happen given enough or infinite time? Does it have to happen eventually?

Physicist: There are a lot of subtleties in this question!  The answer is basically yes, but there are some sneaky assumptions worked into that.

Right off the bat, a probability is always based on “priors”.  For example, “the probability that it will rain today” or “the probability that a 4 will be rolled” are not, completely on their own, well-defined probabilities.

The probability of a particular event is dependent on “priors” or “conditions”.  In order to know the probability of getting a particular result, you must have prior knowledge of what die is being rolled.

Before you can find a probability that’s an actual number, you need to know something about the priors.  The probability that it will rain depends on the place, time, season, whether or not it rained yesterday, etc.  The probability that a 4 will be rolled depends on what kind of die is being rolled, if it’s weighted, or even if dice exist.

In this general case, you may have a tiny, non-zero probability, but if it’s based on priors that are themselves impossible, then the event itself may also be impossible.  You can generalize the priors a lot, but you can never quite get rid of all of them.  For example, it may be possible to prove, beyond a shadow of a doubt, that the probability that a unicorn is violent is 5%, given that unicorns exist (when a scientist says “given”, they’re about to spit out some priors).  However that doesn’t guarantee that a violent unicorn must exist, because it requires that unicorns (with their magic, and virgin sensing powers, and whatnot) must already exist in general.

But (and this may be more at the heart of the question), given an infinitely large universe that’s more or less homogeneous (lots of “stuff”, like the part of the universe we can see with telescopes, instead of just being empty forever), then pretty much anything that’s remotely possible, that could conceivably be the result of a string of remotely possible causes (e.g., horse begets unicorn begets violent unicorn), will happen somewhere.

As a slightly less fantastical example, we can imagine creating, say, an array of Tinker Toys™ linked together and spanning light-years of space.  If this could be instantaneously constructed, somehow teleported into existence, then it would continue to exist for a little while (its self-gravity would start to crush it in fairly short order).  It is not, by itself, an impossible configuration of stuff.

Light years of tinker toys. Its existence is possible, but there is no set of circumstances that would lead to it happening.

However, due to laws like the conservation of mass, the light-speed speed limit, and the nature of gravity, there’s no way to put together a structure this big and massive (or for it to form naturally).  Long before you even got to the business of connecting everything together you’d find that there was already far too much mass, far too close together.  No matter how fast you tried to get everything in place you’d find that the arrangement is smaller than its own Schwarzschild radius, which means that a Tinker Toy™ construction of this size and density is already a black hole (“teleporting it together” gives it a little time because no part of it would “know” that it was too big for a while).

So, we can sit back as say things like, “well, there are X many possible arrangements of atoms, or quantum states, or whatever, and this is one of them…” and can then calculate a ball-park estimate of the probability of this massive wooden grid existing (“1/X” maybe?).  Unfortunately, the answer we’d get would be incorrect, because the priors are messed up.  While it could exist, it could not be formed.  So simply knowing that something is “possible” doesn’t mean that the universe can ever be in a state that would eventually lead to that thing happening.

As far as happening eventually: if it’s not happening now (in an infinite universe), it almost certainly never will.

The tinker toy picture is of a “clockwork” tick-tac-toe playing computer.

Posted in -- By the Physicist, Philosophical, Probability | 65 Comments

Q: Which of Earth’s life forms could survive on each planet of the Solar System?

Posted on December 13, 2012 by The Physicist

Physicist: We can feel fairly certain that no life from Earth can survive on the surface of any of the other planets.

Mercury is really inhospitable.  Although there’s some water ice in craters near it poles, there’s very little hope of any liquid water anywhere.

Venus may be capable of sustaining high-altitude microbes (where it’s relatively cool), but nothing can survive being anywhere close to the surface (including robots, the sturdiest of which have lasted for about 2 hours).  That said, even the high-atmosphere life here on Earth is still dependent on the biosphere below.

Earth is alright.  Could be better.

If there’s liquid water deep under the surface of Mars there are a few extremophiles that may be able to survive there.

Given the extreme cold, or pressure, or toxic gases of all of the gas giants, it’s very unlikely that anything could survive on/in them.  Jupiter, Saturn, Uranus, and Neptune all suffer from the same affliction: no ground.  It may be possible to engineer some kind of amazingly hardy space-kelp, that uses bladders filled with harvested hydrogen to float in the warmer layers of the gas giants, and somehow gleans energy from the almost completely chemically inert atmospheres and the very un-Sunny darkness.

Unfortunately, space-kelp doesn’t exist (yet).

An artist’s conception of Jupiter space-kelp growing under water.

The dwarf planets are a dry well as far as survivability goes.  They’re too small to hold an atmosphere or have warm cores (as far as we know).  So, Ceres, Pluto, Sedna, Xena (and its moon Gabriel), and all the rest would be great places to mummify creatures in a hurry, but not much else.

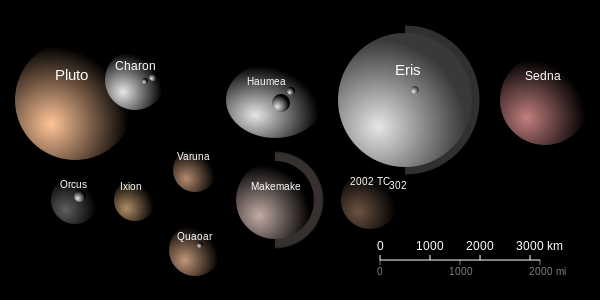
Some of the dwarf planets. Most of these are far to small and distant for us to have decent images, but in 2015 New Horizons will give us some detailed images of Pluto and Charon!

So the other planets and dwarf planets are a bust.  However, there are moons aplenty in the solar system.  Titan has an atmosphere even denser than ours (this is freaking researchers right-the-heck-out today), and many other moons have active, hot cores.  There may be some bacteria that could live in the methane-rich environment of Titan, assuming they could find a place warm enough under the surface to find some liquid water (the surface of Titan is almost cold enough for liquid nitrogen to condense out of its atmosphere), but they wouldn’t exactly thrive.

Another hope is Europa, an big ball of ice that may have liquid water oceans beneath its frozen surface.  As far as I know, this is the only place that anyone is expecting to find life that might be even remotely familiar to us.  Assuming it does have volcanically heated water, Europa may also be the only place with even the slightest possibility of multi-cellular life.

Europa: Crunchy and icy on the outside, and possibly life-supporting just inside.

That said, it probably doesn’t.  It’s fairly likely that living things from Earth have been blasted into space (by impacts) and have eventually landed on almost every major body in the solar system.  While it’s possible to survive the trip, living and growing on another planet is likely to be impossible.

Posted in -- By the Physicist, Astronomy, Biology | 12 Comments

Q: What are fractional dimensions? Can space have a fractional dimension?

Posted on December 8, 2012 by The Physicist

Physicist: There are a couple of different contexts in which the word “dimension” comes up.  In the case of fractals the number of dimensions has to do (this is a little hand-wavy) with the way points in the fractal are distributed.  For example, if you have points distributed at random in space you’d say you have a three-dimensional set of points, and if they’re all arranged on a flat sheet you’d say you have two-dimensional set of points.  Way back in the day mathematicians figured that a good way to determine the “dimensionality” of a set is to pick a point in the set, and then put progressively larger and larger spheres of radius R around it.  If the number of points contained in the sphere is proportional to Rd, then the set is d-dimensional.

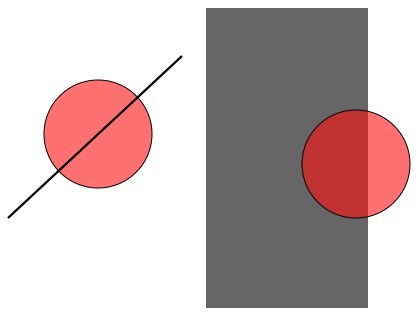
(Left) as the sphere grows, the number of points from the line that it contains increases like R, so the line is one-dimensional. (Right) as the sphere increases in size the number of points from the rectangle that it contains increases like R2, so the square is two-dimensional.

However, there’s a problem with this technique.  You can have a set that’s really d-dimensional, but on a large scale it appears to be a different dimension.  For example, a piece of paper is basically 2-D, but if you crumple it up into a ball it seems 3-D on a large enough scale.  A hairball or bundle of cables seems 3-D (by the “sphere test”), but they’re really 1-D (Ideally at least.  Every physical object is always 3-D).

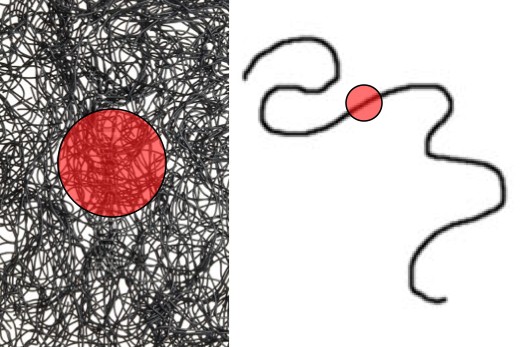
A “crumpled up” set seems like it has a higher dimension than it really does.  You can get around this by using smaller and smaller spheres.  Eventually you’ll get the correct dimension.

This whole “look at the number of points inside of tiny spheres and see how that number scales with size” thing works great for every half-way reasonable set.  However, fractal sets can be “infinitely crumpled”, so no matter how small a sphere you use, you still get a dimension larger than you might expect.

The edge of the Mandelbrot set “should” be one-dimensional since it’s just a line. However, it’s infinitely twisty, and no matter how much you zoom in it stays just as messed up.

When the “sphere trick” is applied to tangled messes it doesn’t necessarily have to give you integer numbers until the spheres are small enough.  With fractals there is no “small enough” (that should totally be a terrible movie tag line), and you find that they have a dimension that’s often a fraction.  The dimension of the Mandelbrot’s boundary (picture above) is 2, which is the highest it can be, but there are more interesting (but less pretty) fractals out there with genuinely fractional dimensions, like the “Koch snowflake” which has a dimension of approximately 1.262.

The Koch snowflake, which is so messed up that it has a dimension greater than 1, but less than 2.

That all said, when somebody (looking at you, all mathematicians) talks about fractional dimensions, they’re really talking about a weird, abstract, and not at all physical notion of dimension.  There’s no such thing as “2.5 dimensional universe”.  When we talk about the “dimension of space” we’re talking about the number of completely different directions that are available, not the whole “sphere thing”.  The dimensions of space are either there or not, so while you could have 4 dimensions, you couldn’t have 3.5.

Posted in -- By the Physicist, Math | 14 Comments

Q: Are shadows 2-dimensional? Are there any real examples of 2-dimensional things in the universe?

Posted on December 3, 2012 by The Physicist

Physicist: If you think of a shadow as the lack of light created by an object blocking a light source, then shadows are 3-D.  After all, it’s dark everywhere behind an object, not just on the surface of another object.

Is a shadow the dark volume behind stuff, or the dark surface on other things?

If, on the other hand, you define a shadow to be what we see and intuitively think of (the dark, parroting person on the wall, with whom you can shadow box) and not the volume in between, then shadows are 2-D.

However, that second definition is a little abstract, because there’s no real physical significance.  You could say that the border between countries is a one dimensional line along the ground, but there are no physical laws that have anything to do with national borders, so it doesn’t matter.

Defining exactly where the surface of an object is (what with all of their atoms) is like trying to define exactly where the surface of a ball pit is.

It’s impossible to get something that’s genuinely 2-D in our universe for several reasons, the simplest of which is that atoms themselves are 3-D.  So even the flattest flat thing will still have some 3-D-ness (at least a quarter of a nanometer or more).  That said, there are innumerable examples of things that behave as though they were 2-D.  In situations where one direction is restricted compared to the others you’ll often find that the physics follows suit.

Hurricanes and other very-large-scale weather phenomena roughly obey 2-dimensional physics.

For example, ripples on the surface of water are an example of 2-D waves that behave very differently from ordinary 3-D waves.  Weather systems that are substantially bigger across than they are tall, like hurricanes (e.g., Sandy was about 800 miles across, and only about 5-10 miles high), roughly obey 2-D fluid dynamics.  Normally the energy in a fluid (or gas) starts out with big eddies and moves into smaller and smaller eddies (you can see this if you pour cream into some coffee and then stare at it).  However, very weirdly, in a 2-D fluid you find that the opposite tends to be true: energy starts out in small eddies and moves to larger.

If it weren’t for the flatness of the atmosphere (and some obscure math involving “entropy flow” in 2-D fluids) we wouldn’t get hurricanes!

Posted in -- By the Physicist, Physics | 26 Comments

Q: Is it possible to experience different rates of time? If time were to speed up, slow down, or stop, what would you experience?

Posted on November 28, 2012 by The Physicist

Physicist: It depends a little on how you define “experience”, but in general you’ll always experience time moving in exactly the same way.  So sci-fi movies where the characters are experiencing slowed-down or sped-up time and are having a hard time moving around because time is all messed up are extremely inaccurate.  Outside of conversations that start with “I think it’s kicking in” you’ll never talk to anybody about how time is moving too fast or slow.

The mechanisms behind how our brains work, and by extension how we think, are governed by the same “kind of time” as everything else (known commonly as “time”).  So, if time “gets stretched out” by a factor of two, then the way our brain experiences it will also be stretched out by a factor of two.  Time would seem to be passing normally, even though everyone outside of the “time bubble” would see you differently.  In fact, there’s a few pretty decent sci-fi books about exactly that.

In a nutshell, time always passes at exactly one second per second.  Even if time were to suddenly stop and start again, there’s be no way to tell (except to check in with someone unaffected).

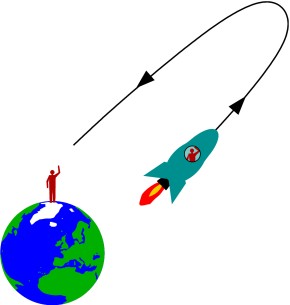
The twin paradox, where someone (doesn’t have to be a twin) moves around quickly for a while and finds that less time has passes for them than for their non-moving compatriots.

So what about when physicists, with their non-ironic beards, talk about time slowing down at high speeds according to special relativity?  Relativity is a theory about (not to surprisingly) relative movement and its effects.  The “twin paradox“, is a real-world example of time genuinely passing at different rates for different observers (although the mechanics of exactly who saw what and why takes a little hashing out).  However, without exception, in all of the examples from physics in which time passes at different rates, it’s always someone else’s time that’s affected.  Everyone (everything) involved always sees their own time passing normally.

There’s an unfortunate weakness of language when talkin’ physics.  When a physicist talks about “experiencing time”, what they mean is time as measured by a clock (or any kind of time measuring device).  When your average dude-on-the-street talks about experiencing time, there’s a good chance they’re talking about it in the “a watched pot never boils” kind of way.  Different people and creatures, what our different moods and biochemistry, perceive the passage of time differently, but “real time” is immutable.

The noble banana slug and the morally ambiguous basilisk lizard always experience the same amount of time physically, they just get a different amount done over that same time period.

So, if you see some critters moving quickly and others moving slowly, they’re all experiencing the same amount of time, they’re just using it differently.  By the way, even the fastest creatures aren’t generating any relativistic effects (not even close), different time rates are all in their head.  What’s deeply weird is that different creatures and even different people can genuinely think at extremely different rates!  For example, in this link (←) Oliver Sacks describes a dude who sometimes perceives the passage of only one or two seconds during a two hour period.

The picture of the noble banana slug is from here, and the basilisk lizard is from here.

Posted in -- By the Physicist, Philosophical, Physics, Relativity | 18 Comments