Mathematician:
Suppose you’re interested in answering a simple question: how effective is aspirin at relieving headaches? If you want to have conviction in the answer, you’ll need to think surprisingly carefully about how you approach this question. A first idea might simply be to take aspirin the next time you get a headache, and see if it goes away. But as we’ll see, that won’t be nearly enough.
First of all, since all headaches go away eventually, whether it disappears isn’t the relevant question. It would be better to ask how quickly the headache goes away. But even this phrasing doesn’t capture what you care about, because even if aspirin doesn’t relieve your headache completely, a significant reduction in pain is still worthwhile.
To deal with this issue, you settle on the following plan. When you next get a headache, you’ll make a record of how you feel when it first starts. Then, you’ll take an aspirin, wait 30 minutes, and record how you feel again. You’ll write things like “dull, throbbing pain of low intensity” or “sharp, searing pain over one eye”.
Unfortunately, just examining how you feel after taking aspirin a single time won’t be adequate, since the aspirin may be more helpful some times and less helpful others. For example, it could be the case that it works on moderate headaches but not on severe ones, so if your next headache happened to be really severe, it would look like aspirin was useless. To solve this problem, and give yourself more data, you might resolve to make these records of how you’re feeling for each of the next 20 headaches you get.
There is still a problem though. These subjective descriptions of headaches are difficult to compare to each other. It you take aspirin and your headache goes from a sharp pain over one eye to an intense ache over the entire head, have you made things better or worse? It would be difficult to aggregate the information from these varied descriptions over 20 different headaches to make a final assessment of how well aspirin is working.
Your analyses would be a lot simpler if you scored how unpleasant each headache was on a simple scale from 1 to 5 (1 meaning slight unpleasantness, 3, moderate unpleasantness, and 5, extreme unpleasantness). That way, you can simply look at all the scores you got just before taking aspirin and average them together. You can then compare this to the average of the scores 30 minutes after taking the aspirin. That way, you can see if the amount of unpleasantness you feel really does drop substantially.
Recall that our goal here is to determine how effective aspirin is at relieving headaches, but all you’ve investigated so far is measure how good it is at relieving your own headaches. Perhaps you are more or less sensitive to aspirin than other people, or perhaps your headaches are more severe and harder to treat than most other people’s. To solve this problem, you enlist 40 people who are frequent headache sufferers. You get them to agree that, over the next 6 months, any time they begin to notice that they have a headache they will record how they feel on your 1 to 5 scale. They will then take aspirin and record how they feel 30 minutes later.
But what if people take different doses? You might think that the aspirin isn’t working for some of them, but it’s only because they haven’t taken enough. To fix this problem, you hand them each an identical bottle of pills and tell them to take two whenever they get a headache (the maximum recommended dose, so that if aspirin does work you’ll be using a high enough dose to detect the effects, but not putting people at significant risk of side effects). Handing out aspirin bottles also has the added benefit that everyone will be taking the same brand. That way if you find out that the aspirin really does work, other people can try to replicate your results by using the same brand you did. To make your experiment even better, you also provide everyone with a timer, to help them be more accurate about recording their pain 30 minutes after a headache starts.
There is still a problem though. You know that headaches sometimes become less severe within 30 minutes or so even when left untreated. That means that even if someone’s pain score tends to have fallen 30 minutes after taking the aspirin, you don’t really know whether it is the medicine that caused the reduction in pain or if it would have occurred regardless. To remedy this, you decide that only half of the 40 participants will take aspirin when they have a headache (the rest taking nothing), though everyone will still keep a record of their pain. Then, to see how well the aspirin worked, you can compare the average pain scores of the 20 people who took the aspirin with the scores of the 20 people who didn’t. If the aspirin group’s pain fell a lot more than the non-aspirin group, it would seem then that the aspirin probably was the cause.
But is it possible that the pain levels people record could be influenced by the act of taking a pill, independent of the chemical effect of the active ingredients? Perhaps since people expect aspirin to work, the people in the group taking the pills are more aware of signs of improvement. Or perhaps people’s expectations of improving can even influence how much pain they experience. If either of these things are true, the aspirin might seem to work better than it really does, because some of the reported improvement would be coming from expectations people have about the chemical, rather than just the chemical itself.
Fortunately, this problem is easily fixed. Instead of giving half the people nothing, you instead give that half pills in an aspirin bottle that look just like aspirin, but which are known to have no effect on headaches. Sugar pills are a good choice because they are cheap and free of side effects, and because a small amount of sugar is unlikely to alter a person’s headaches.
This raises ethical considerations. People might agree to take aspirin, but that doesn’t mean they are willing to take sugar pills. So before you start your study, you’ll need to tell everyone that there is a 50% chance they won’t be getting medication. You can’t let them know which kind of pill they got until after the analyses is over though, because that could skew your results. You’ll also want to get them to agree to not take any other headache medication during the experiment.
So half of your group (20 people) will be taking aspirin, and the other half (another 20 people) will get sugar pills. But who should get which? If, for example, the 20 people getting aspirin have headaches that typically last much longer than those of the 20 people that aren’t getting anything, it could make aspirin seem less effective than it really is. So, if possible, you don’t want there to be any substantial differences between the two groups of people. A simple way to make sure this sort of thing is unlikely is to use a computer to randomly assign individuals to the two groups.
It is even better if someone else is in charge of this te randomization (secretly recording which person is assigned to which type of pill). That way, when you talk to the subjects about the experiment, there is no chance that you accidentally tip them off (with body language, or subtle cues) to which type of pill they are getting. Furthermore, when you analyze the final results, you won’t have the temptation to make the data come out a particular way (since you won’t know until you are done which subject was taking the aspirin and which was taking the sugar pill).
Unfortunately, even with all the precautions, if you carried out this experiment on multiple occasions, you’d get somewhat different results every time. Even if you used the same study participants, the intensity of their headaches might vary from one 6 month period to the next, which would influence how the results turn out.
But, if the results fluctuate randomly, that implies that sometimes, just by luck alone, the aspirin might seem to be effective even if it isn’t. Likewise, the aspirin might, through bad luck, seem to be ineffective, even though it does work. So whatever your experiment shows, how can you be sure you’re getting the right answer?
Unfortunately, since chance is involved, certainty is not possible. But a statistician can easily calculate for you the probability that you would get results (in favor of aspirin reducing headache pain) that are at least as strong as the ones that you got, if in fact aspirin is no more effective than the sugar pill. If this probability is large, then based on your experiment you do not have sufficient evidence to conclude that aspirin helps headaches. If this probability is small (say, less than 5%), then aspirin likely is effective. In order to increase the likelihood that the results of your test are conclusive, you would need only to increase the number of participants involved.
We see that to answer questions with a high degree of certainty, a well thought out approach is necessary. Most elements of good study design become obvious when we reflect logically on the ways that data may mislead us. When possible, experiments should be triple-blind (the study participants, researchers, and statisticians all should not know who is receiving each treatment). A control group should be used, consisting either of a placebo control, or another treatment whose effectiveness is already know. Studies should have large sample sizes (20 participants in each treatment group, at the bare minimum). They should use standardized dosages, and should apply a standardized (and predetermined) method for measuring results. They should employ careful statistical analyses.
Unfortunately, many studies don’t follow these important rules. But without such rules, studies are hard to trust, even when they’re just trying to answer a simple question about aspirin.
, where
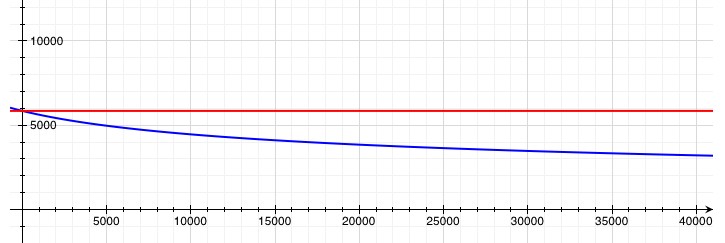
is the rate of heat loss, T is the surface temperature, S = 6×1018m2 is the surface area, and σ = 5.67×10-8 is a physical constant. If we assume that the surface temperature is proportional to the average temperature within the Sun (which is presently about 4 million °K), then we can find a relationship between the surface temperature, T, and the total heat energy, q. This is a bad assumption over the long run, but should be decent enough for figuring out how long it would take the Sun to lose, say, 1% of its heat.
. It doesn’t take much to end all life on Earth, so we would probably have, at most, a couple million years. It would take a little over one hundred thousand years for the surface temperature of the Sun to drop by 1%.