Q: What is a Fourier transform? What is it used for?

Posted on September 24, 2012 by The Physicist

Physicist: Almost every imaginable signal can be broken down into a combination of simple waves.  This fact is the central philosophy behind Fourier transforms (Fourier was very French, so his name is pronounced a little wonky: “4 E yay”).

A complicated signal can be broken down into simple waves.  This break down, and how much of each wave is needed, is the Fourier Transform.

Fourier transforms (FT) take a signal and express it in terms of the frequencies of the waves that make up that signal.  Sound is probably the easiest thing to think about when talking about Fourier transforms.  If you could see sound, it would look like air molecules bouncing back and forth very quickly.  But oddly enough, when you hear sound you’re not perceiving the air moving back and forth, instead you experience sound in terms of its frequencies.  For example, when somebody plays middle C on a piano, you don’t feel your ear being buffeted 261 times a second (the frequency of middle C), you just hear a single tone.  The buffeting movement of the air is the signal, and the tone is the Fourier transform of that signal.

The layout of the keys of a piano (bottom) are like the Fourier transform of the sound the piano makes (top).

The Fourier transform of a sound wave is such a natural way to think about it, that it’s kinda difficult to think about it in any other way.  When you imagine a sound or play an instrument it’s much easier to consider the tone of the sound than the actual movement of the air.

An example of a Fourier transform as seen on the front of a sound system.

In fact, when sound is recorded digitally the strength of the sound wave itself can be recorded (this is what a “.wav” file is), but more often these days the Fourier transform is recorded instead.  At every moment a list of the strengths of the various frequencies is “written down” (like in the picture above).  This is more or less what an mp3 is (with lots of other tricks).  It’s not until a speaker has to physically play the sound that the FT is turned back into a regular sound signal.

Older analog recording techniques, like this vinyl record, record the original sound signal and not the FT.

In the form of an FT it’s easy to filter sound.  For example, when you adjust the equalizer on your sound system, like when changing the bass or treble, what you’re really doing is telling the device to multiply the different frequencies by different amounts before sending the signal to the speakers.  So when the base is turned up the lower frequencies get multiplied by a bigger value than the higher frequencies.

However, acoustics are just the simplest application of FT’s.  An image is another kind of signal, but unlike sound an image is a “two dimensional” signal.  A different kind of FT can be still found, and it is likewise two dimensional.  When  this was first done on computers it was found that, for pretty much any picture that isn’t random static, most of the FT is concentrated around the lower frequencies.  In a nutshell, this is because most pictures don’t change quickly over small distances (something like “Where’s Waldo?” would be an exception), so the higher frequencies aren’t as important.  This is the basic idea behind “.jpeg” encoding and compression (although there are other clever tricks involved).

An image and its Fourier transform. Notice that most of the FT is concentrated in the center (low frequencies). Deleting the FT away from the center saves a lot of data, and doesn’t do too much damage to the image. This is called a “low-pass filter”.

Interesting fun fact: the image of the woman in the hat is called “Lenna” and it’s one of the most commonly used standards in image-processing tests.  It’s the top half of a adult image, and while it may seem strange that computer scientists would use that sort of image, the argument can be made that most comp-sci students don’t have too much experience finding any other kind.

While digital technology has ushered in an explosion of uses for Fourier transforms, it’s a long way from being the only use.  In both math and physics you find that FT’s are floating around behind the scenes in freaking everything.  Any time waves are involved in something (which is often), you can be sure that Fourier transforms won’t be far behind.  It’s commonly easy to describe something with a single, simple wave, like pendulums or a single bouncing ball.  Often (but certainly not always) it’s possible to break down complex systems into simple waves (or to approximately do this), then to look at how those waves behave individually, and then to reconstruct the behavior of the system as a whole.  Basically, it’s easy to deal with “sin(x)” but difficult to deal with a completely unknown function “f(x)”.

Physicists jump between talking about functions and their Fourier transforms so often that they barely see the difference.  For example, for not-terribly-obvious reasons, in quantum mechanics the Fourier transform of the position a particle (or anything really) is the momentum of that particle.  Literally, when something has a lot of momentum and energy its wave has a high frequency, and waves back and forth a lot.  Applying Fourier stuff to quantum mechanics is one of the most direct ways to derive the infamous Heisenberg Uncertainty principle!  FT’s even show up in quantum computers, as described in this shoddily written article.

Mathematicians tend to be more excited by the abstract mathematical properties of Fourier transforms than by the more intuitive properties.  A lot of problems that are difficult/nearly impossible to solve directly become easy after a Fourier transform.  Mathematical operations on functions, like derivatives or convolutions, become much more manageable on the far side of a Fourier transform (although, more often, taking the FT just makes everything worse).

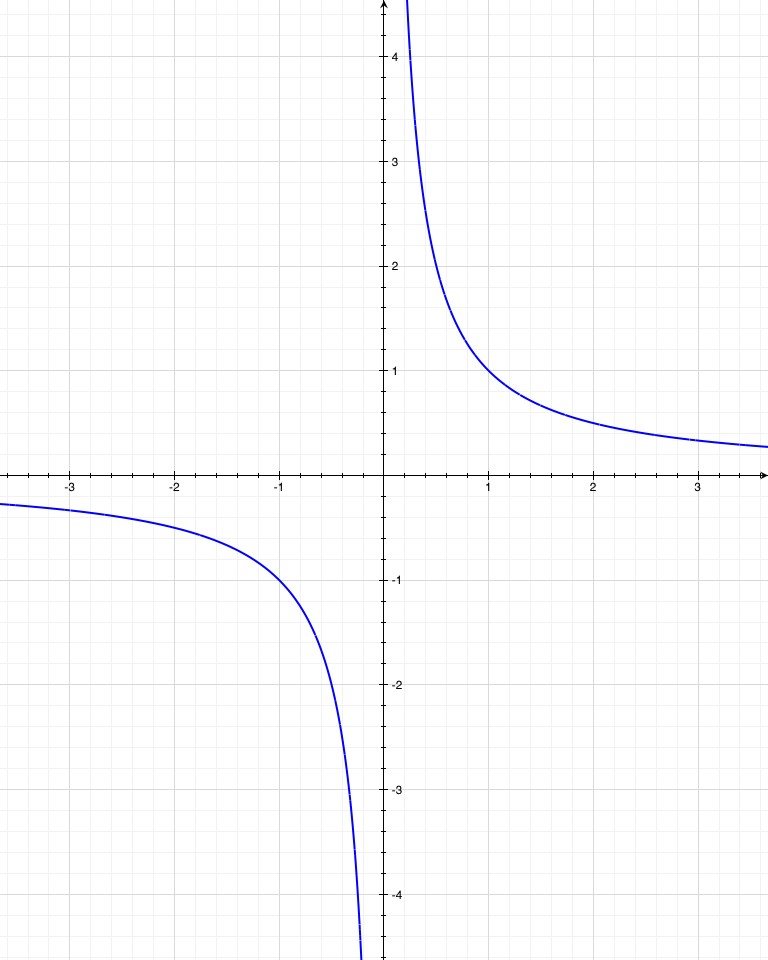
Answer gravy: Fourier transforms are of course profoundly mathematical.  If you have a function, f, that repeats itself every 2π, then you can express it as a sum of sine and cosine waves like this: f(x) = \sum_{n=0}^\infty A_n\sin{(nx)}+B_n\cos{(nx)}.

It turns out that those A’s and B’s are fairly easy to find.  Sines and cosines have a property called “orthogonality”.

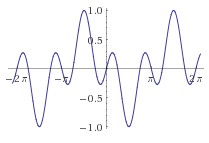
f(x) = sin(x)cos(2x). The orthogonality of sines and cosines is a statement about the fact that mixing sines and cosines of different frequencies creates functions that are positive exactly as often as they are negative (zero on average).

\begin{array}{ll}\int_{0}^{2\pi}\cos{(nx)}\sin{(mx)}dx&=0\\\int_{0}^{2\pi}\cos{(nx)}\cos{(mx)}dx & =\left\{\begin{array}{ll}\pi&,m=n\\0 & ,m\ne n\end{array}\right.\\\int_0^{2\pi}\sin{(nx)}\sin{(mx)}dx&=\left\{\begin{array}{ll}\pi&,m=n\\0&,m\ne n\end{array}\right.\end{array}

Now, say you want to find out what B3 is (for example).  Just multiply both sides by cos(3x), and integrate from 0 to 2π.

\begin{array}{ll}f(x)=\sum_{n=0}^\infty A_n\sin{(nx)}+B_n\cos{(nx)}\\\smallskip\Rightarrow f(x)\cos{(3x)}=\sum_{n=0}^\infty A_n\sin{(nx)}\cos{(3x)}+B_n\cos{(nx)}\cos{(3x)}\\\smallskip\Rightarrow \int_0^{2\pi}f(x)\cos{(3x)}dx=\int_0^{2\pi}\left[ \sum_{n=0}^\infty A_n\sin{(nx)}\cos{(3x)}+B_n\cos{(nx)}\cos{(3x)}\right]dx\\\smallskip =\sum_{n=0}^\infty A_n\int_0^{2\pi}\sin{(nx)}\cos{(3x)}dx+B_n\int_0^{2\pi}\cos{(nx)}\cos{(3x)}dx\\\smallskip = B_3\int_0^{2\pi}\cos{(3x)}\cos{(3x)}dx\\\smallskip = \pi B_3\end{array}

You can do this for all of those A’s and B’s, so A_n =\frac{1}{\pi}\int_0^{2\pi}f(x)\sin{(nx)}dx and B_n =\frac{1}{\pi}\int_0^{2\pi}f(x)\cos{(nx)}dx.

Taking advantage of Euler’s equation, eiθ = cos(θ) + i sin(θ), you can compress this into one equation: f(x)= \sum_{n=0}^\infty C_n e^{inx}, C_n = \frac{1}{\pi}\int_0^{2\pi}f(x)e^{inx}dx.  There are some important details behind this next bit, but if you expand the size of the interval from [0, 2π] to (-∞, ∞) you get:

f(x) = \int\hat{f}(n)e^{i2\pi nx}dn and \hat{f}(n) = \int f(x)e^{-i2\pi nx}dx  Here, instead of Cn, you have \hat{f}(n) and instead of a summation you have an integral, but the essential idea is the same.  Here, \hat{f}(n) is the honest-to-god actual Fourier transform of f.

Now here’s a big part of why mathematicians love Fourier transforms so much that they want to have billions of their babies, naming them in turn, “baby sub naught, baby sub one, through baby sub n”.

If you’re looking at a differential equation, then you can solve many of them fairly quickly using FT’s.  Derivatives become multiplication by a variable when passed through a FT.  Here’s how:

\begin{array}{ll}\int f^{\prime}(x)e^{-2\pi i n x} dx\\\smallskip =-\int f(x)\frac{d}{dx}\left[e^{-2\pi i n x}\right] dx + f(x)e^{-2\pi i n x}|_{-\infty}^{\infty}\\\smallskip =-\int f(x)\frac{d}{dx}\left[e^{-2\pi i n x}\right] dx\\\smallskip =-\int f(x)(-2\pi i n)\left[e^{-2\pi i n x}\right] dx\\\smallskip =2\pi i n\int f(x) e^{-2\pi i n x}dx\\\smallskip =2\pi in \hat{f}(n)\end{array}

Suddenly, your differential equation becomes a polynomial!  This may seem a bit terse, but to cover Fourier transforms with any kind of generality is a losing battle: it’s a huge subject with endless applications, many of which are pretty complicated.  Math’s a big field after all.

 

The record groove picture is from here.

The Lenna pictures are from here.

The top picture with the four scientists is from here.

Posted in -- By the Physicist, Equations, Math | 40 Comments

Q: What are singularities? Do they exist in nature?

Posted on September 19, 2012 by The Physicist

Physicist: Singularities are just artifacts that fall out of math.  They show up a lot in theory, and (probably) never in nature.  The “singularities” most people have heard of are black hole singularities.

In practice, when you’re calculating something in physics and you find a singularity in your calculation (this happens all the time), which usually looks like “1/x”, then that means that there’s a mistake somewhere, or you’re looking at something that never happens, or there are physical laws or effects that haven’t been taken into account.

The simplest mathematical singularity: 1/x.  The closer you get to zero, the more 1/x blows up, and at x=0 the function is undefined.

For example, when you drain water from a tub or sink the water will spiral into the drain.  A back of the envelope calculation (based on known principles) shows that the speed, s, that the water is moving is s=\frac{c}{r}, where r is the distance to the center of the spin, and c is a constant that has to do with how fast the water was turning before you pulled the plug.  Notice that this equation implies that as water gets closer and closer to the drain, it will move faster and faster, and that right over the drain it will be moving infinitely fast.  So how does the universe find an out?  This will look familiar:

One of the slick tricks that water uses to avoid spinning infinitely fast at the center of a vortex: not being there.

Even when you’re deep underwater there are outs; turbulence, cavitation, that sort of thing.

A slightly more obscure example is the energy of a charged particle’s electric field.  If you have an electron just sitting around, the energy, E, of its field outside of a distance, R, from the electron is E =\frac{e^2}{8\pi\epsilon_0}\frac{1}{R}.

The electric field being considered is the light blue area. The most intense part of the field is close to the electron, so as R gets smaller and smaller, the total energy gets bigger and bigger.

Most of that is just equation porn.  The important bit is the “\frac{1}{R}“.  Once again there’s a mathematical singularity in an equation describing a physical thing.  But, once again, the universe (being sneaky) finds a way out.  This is a hair less intuitive than the whirlpool thing, but in quantum mechanics an electron is described as being “smeared out” (in an uncertainty principle kind of way).  It doesn’t exist in any one place, so the idea of getting infinitely close doesn’t really make sense.

The whirlpool thing and the electron thing (and hundreds of other examples) are examples of singularities that show up in the math, but can be explained away through experiment and observation, and shown to not be singularities in the physical world.

In general relativity, the shape of spacetime near a spherical mass is given by:

c^2 d\tau^2 = \left(1-\frac{r_s}{r}\right)c^2dt^2 - \left(1-\frac{r_s}{r}\right)^{-1}dr^2 - r^2\left(d\theta^2 + \sin^2{(\theta)}d\phi^2\right)

Now, unless you’re already a physicist, none of that should make any sense (there are reasons why it took Einstein 11 years to publish general relativity).  But notice that, as ever, there’s a singularity at r=0.  This is the vaunted “Singularity” inside of black holes that we hear so much about.

Something like a star or a planet doesn’t have a singularity, because this equation becomes invalid at their surface (this equation is about the empty space around a mass).  But, for a black hole the gravity is so intense, and spacetime is messed up so much that it looks as though there’s nothing to stop matter from becoming infinitely dense.  However, unlike the singularity over the drain in your sink, the singularity in a black hole can’t be observed.  Which is frustrating.

I suspect that what we call the singularity in black holes either doesn’t exist (there is some law/effect we don’t know about) or, if cosmic censorship is true, the nature of that singularity both doesn’t matter and can’t be known, since it can never interact with the rest of the universe.  There are some theories (guesses) that would fix the whole “black hole singularity problem” (like spacetime can only get so stretched, or some form of “quantum fuzziness”), but in all likelihood this is just one of those questions that may never be completely resolved.

The whirlpool photo is from here.

Posted in -- By the Physicist, Math, Philosophical, Physics | 23 Comments

Q: Is it likely that there are atoms in my body that have traveled from the other side of the planet, solar system, galaxy, or universe?

Posted on September 13, 2012 by The Physicist

Physicist: Not just likely, but essentially guaranteed!

Technically, every atom in your body has been swirling all around the galaxy for billions of years (although it’s mostly stayed in the same place for the last 5 billion or so).  So whether material is “from space” is really a question of time frame.  We talk about asteroids and meteorites that fall to Earth as “being from space”, but they’re made of the same stuff and have the same origins as the material of the Earth, they’re just a little late to the party.  If you roll back the clock far enough you find that the Earth (or what would become the Earth) was just a big collection of the same dust and rocks that pepper it today.

The water on Earth is constantly being incorporated into, and falling out of, living things.  All of us (people and critters alike) are mostly water.  Likewise, a fair fraction of the stuff you’re most likely to find drifting about in the solar system is water.  Sure, space-rocks have lots of iron and other heavy stuff, but we use very little of that.  Water seems like the most likely material to be from space and in your body.

Life: cleverly put together bags of water.

The water in the biosphere is pretty good at mixing around.  So good in fact, that (excluding permanent ice) it doesn’t even make sense to say that a particular water molecule is from anywhere in particular.  Most of the material in your body has not only been to the far side of the planet, but has probably been there and back many times.

About 20 tons of material (this changes a lot day-to-day) is collected by the Earth every day in the form of space dust, meteors, flakes of ice, etc.  You can find this stuff  everywhere on the planet in the form of tiny spheres of iron (you’d never notice that it looks any different from any other grit without a microscope).

Micrometeorites: they’re freaking everywhere.

Almost all of the that material has been drifting about in the solar system since it formed (at about the same time as the Earth, 5 billion years ago), sequestered inside of comets and asteroids, and has only recently (hundred million years, give or take) been released by collisions or in comet tails or whatnot.

There’s a fairly heated debate about what fraction of the junk drifting around the solar system is made of water, but let’s assume (low-aiming shot in the dark) that about 10% of the 20 tons of stuff that switches from “team space” to “team Earth” every day is water ice.  This sort of thing has been going on since the Earth formed (basically, it’s how the Earth formed).  Also, just to draw a line in the sand, let’s say that stuff that’s arrived on Earth in the last one thousand years is from space and anything around before that is from Earth.  So, that’s about 730,000 tons of “new” water from space.  Which sounds like a lot, but considering that the Earth already has 1,400,000,000,000,000,000 tons of water, it’s just a drop in the bucket.  Specifically, a bucket with lots of water in it.

Even so, atoms are small, and there are a hell of a lot of them.  They get everywhere.

So here comes an actual answer.  About 1 out of every 2 trillion water molecules on Earth (reminder; these are gross estimates), and in our bodies has arrived in the last thousand years.  That means that there is recently-from-space-water in everybody’s body, with one molecule every few dozen cells.

But that’s just water from our own solar system.  Once a star system forms very little new material comes into it.  The vast, vast majority of the stuff in interstellar space is gas and ultra-fine dust, and that sort of thing tends to get blown away by the solar wind of an active star.  The closest that this stuff generally gets is the “heliopause“, which is way out there (somewhere around 100 times farther out than Earth’s orbit).

A “bow shock” created by the interaction of the solar winds produced by the star LL Ori and the interstellar winds of the Orion Nebula.

It’s estimated that only about 0.01% of the dust in the solar system drifted in from interstellar space.  Still!  That’s around 1 part in 20 quadrillon, which means that you should have somewhere around 50 billion water molecules in your body that arrived on Earth in the last thousand years from somewhere outside of the solar system.

Keep in mind that all of these numbers are fairly rough, but not 10-orders-of-magnitude-rough.  There’s totally interstellar space water in you!

Two galaxies in the midst of merging.

Once galaxies form very little matter is exchanged between them.  The exception being when galaxies collide and merge, but the Milky Way hasn’t had a “big meal” in a very long time.  If you think that space in high Earth orbit is empty, brother let me tell you: intergalactic space is… a lot more empty than that.  The atoms in your body that came from other galaxies, almost certainly came from galaxies absorbed by the Milky Way.

Posted in -- By the Physicist, Astronomy, Physics, Probability | 14 Comments

Q: Is there a number set that is “above” complex numbers?

Posted on September 8, 2012 by The Physicist

Physicist: Yes, but they don’t fix problems the way the complex numbers do.

The nice thing about real numbers (which includes basically every number you might think of: 0, 1, π, -5/2, …) is that no matter how you add, subtract, multiply, or divide (other than 0) them together, you always get another real number.  This property is called being “closed”.  A mathematician would say “the real numbers are closed under addition, because any real numbers added together always give you another real number”.

Closed-ness is comforting to have, because it means that when you’re doing basic math, no matter how you jump you’ll always have somewhere to land.  Mathematically speaking.

However!  When you’re doing square roots the real numbers are not closed.  When you ask “\sqrt{x}=?” what you mean is “x=?^2“.  For example, to find \sqrt{4}=?, you just answer the question, ?^2 = 4, and find that the answers are ? = 2 or -2.  But if you try the same thing with \sqrt{-4} you’ll be trying to answer the question ?^2 = -4, which doesn’t have any answers (try it).  To “solve” this problem Euler decided to make up a new “number” called “i“, with the property that i^2=-1, and complex numbers were born.

Every complex number can be written “A+Bi”, where A and B are regular numbers. Notice that when B=0 you’ve got a regular, real number, so the complex numbers include the real numbers.

So here’s where the question comes into play.  i may patch the problem with \sqrt{-1}, but does it just give rise to a new problem when you try to figure out what \sqrt{i} is?  Turns out: no!

\sqrt{i} = \pm(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i)

You can check this by squaring it:

\begin{array}{ll}\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\right)^2\\\smallskip=\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\right)\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\right)\\\smallskip=\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}i^2+\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}i+\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}i\\\smallskip=\frac{1}{2}+\frac{1}{2}i^2+\frac{1}{2}i+\frac{1}{2}i\\\smallskip=\frac{1}{2}-\frac{1}{2}+\frac{1}{2}i+\frac{1}{2}i \\\smallskip=i\end{array}

Weirdly enough, there is absolutely no combination of roots/exponentiations or multiplications/divisions or additions/subtractions that can break out of complex numbers.  Where the closed-ness of real numbers fail, complex numbers hold strong.  This is one of the important aspects of the “fundamental theorem of algebra“.  You can tell mathematicians think it’s important, they don’t call just anything the “fundamental theorem of whatever”.

Finally, here’s the answer, there are a lot of (infinite) number-systems bigger than the complex numbers that contain the complex numbers in the same way that complex numbers contain the real numbers.  However, they’re not “needed”.

The smallest number system that’s bigger than the complex numbers is the “quaternions”.  The real numbers can be built from “1” and then seeing what you can get from any combination of adds, multiplies, etc. (and then filling in the gaps).  Complex numbers can be built the same way, starting with “1” and “i”.  Quaternions are built out of 1, i, j, and k.  i, j, and k all do basically the same thing that i does in complex numbers; i^2=j^2=k^2=-1.  In addition, ij=k, jk=i, ki=j, and if you flip the order you flip the sign, so ji=-k.

Quaternions don’t “patch holes” that the complex numbers have, but they do help with some very complicated problems that other number-systems can’t handle easily.  To head off the next obvious question; yes, there are even larger number-systems, like the “octonians“, and inventing ever higher systems is easy enough.

The graph is a picture from here.

Posted in -- By the Physicist, Math | 12 Comments

Q: Are the brain and consciousness quantum mechanical in nature?

Posted on September 3, 2012 by The Physicist

Physicist: The extremely short, smart-ass answer to this is: of course!  Ultimately everything in the universe is built out of tiny quantum things and ultimately everything obeys quantum mechanical laws.  But that’s not really the spirit of the question, and it doesn’t tell you anything useful.  You could just as easily say that computers take advantage of the same principles behind lightning (electricity), but that doesn’t tell you anything about computers or lightning.

The “connection” between quantum physics and consciousness is pretty famous these days, what with the Secret, Chopra, and stuff like that.  Unfortunately, in legit science we don’t have a real, solid definition for consciousness, which makes talking about it a little tricky.  To a physicist, consciousness is like obscenity; you know it when you see it.  So, while I can’t speak to what consciousness is, I can say it doesn’t seem to have any influence on quantum phenomena (at least, outside of the head).  The brain, on the other hand, can be defined (you can even point at it!), and the brain definitely involves quantum mechanics.  Chemistry, which is arguably the most important part of biochemistry, is all about quantum mechanics.

But are more interesting quantum effects, like entanglement, quantum teleportation, and quantum computation used by the brain?  It seems unlikely, since quantum experiments done in the lab are generally done in very, very carefully controlled, usually cold, environments, involving just a few atoms at a time.  By contrast, brains involve many atoms (like… dozens) and are generally warm, and squishy, and very un-lab-like.  Any zombie scientist will say the same.  And yet the surprising, somewhat hesitant, answer is a resounding: maybe! Recently it’s been shown that many (possibly all) plants use a form of “quantum search”

Plants: natural quantum computers?

So far, photosynthesis is the best example of coherent quantum phenomena (stuff involving entangled or controlled states across multiple atoms) in biology, but it’s exciting enough to give rise to the new field of “quantum biology”.

Generally speaking, “coherent states” (which are the kind of nice, clean quantum states you need to have entanglement or any of the other weirder quantum effects) get broken apart in environments as noisy as a biological system.  But there are some very slick tricks being used by physicists to over-come noise, like topological quantum computation, quantum error-correcting codes, and robust states (clever combinations of states that are more stable than their constituent states).

It may be that, like chloroplasts in plants, our brains have some cute tricks for maintaining coherent states and possibly computing with them. Weirder things have happened (maybe not a lot weirder). For example; among the many other things they do, ours eyes are continuously running an edge-detection algorithm and our ears preform a physical Fourier transform.  So far we’ve only scratched the surface of what kind of tricks our brains use, literally.  It’s tricky to study the inside of a brain while keeping it alive, so we know a lot about the eyes, ears, nose, and peripheral nervous system, but surprisingly little about how that information is processed in the brain.

There’s a subtle but important difference between quantum mechanics and magic. So, even if our brains are capable of handling quantum information on a large scale, we can’t expect to have any cool powers because of it. The brain might use entanglement to correlate things on different sides of the brain, or rapidly organize information. But as for cooler things, like telepathy, or clarvoiance, or any kind of film-worthy mental powers: nope!

Posted in Biology, Philosophical, Physics, Quantum Theory | 11 Comments

Q: How are voltage and current related to battery life? What is the difference between batteries with the same voltage, but different shapes or sizes? What about capacitors?

Posted on August 29, 2012 by The Physicist

Physicist: Chemical batteries use a pair of chemical reactions to move charges from one terminal to the  other with a fixed voltage, usually 1.5 volts for most batteries you can buy in the store (although there are other kinds of batteries). The chemicals in a battery litterally strip charge away from one terminal and deposite charge on the other. In general, the more surface area the chemicals have to deposit charge onto, and take charge away from, the higher the current the battery can produce.

The best way to represent the way a real battery works is to replace the battery in a circuit with an ideal voltage source (which is what we usually think of batteries as being) and an imaginary resistor called the battery’s “internal resistance“.  The internal resistance can be used to describe why an AA battery is incapable of generating an arbitrary amount of power; the more current that the battery creates, the more the voltage across the internal resistor drops according to Ohm’s_law (V=IR). You can picture this as being a little like pushing a cart; if the cart isn’t moving you can really put your shoulder into it, but as the cart moves faster it becomes harder and harder to apply force to it.

A car battery only produces 12 volts, which is the same as 8 ordinary batteries in series.  That voltage is so low that you can put your dry hands on the terminals of a car battery and feel nothing (please don’t trust me enough to try it; I don’t even trust me enough to try it).  And yet the internal resistance is so low that if you connected the terminals with a normal wire, the current in the wire would be so high that the wire would melt or explode.

You can model the way a battery dies by increasing the internal resistance.  A nearly dead battery still provides 1.5 volts, but has a very high internal resistance so that drawing even a trickle of current zeros out the voltage gain.

The voltage across a capacitor on the other hand is always proportional to the charge presently stored in the capacitor (this is the defiition of capacitance). You can think of a battery as being like a water pump, always providing the same pressure, and a capacitor as being like a water ballon, the pressure increasing the more water is in the ballon. The amount of energy in a capacitor is much easier to measure because of this (if you can measure the voltage across it, you can know the energy immediately).  But, because the voltage supplied by a capacitor changes dramatically as it drains, special adaptive circuits are needed to step down the voltage to a fixed, consistent level in order to power a device.  Alternatively, the device can be made to work over a wide range of voltages, but that tends to be more difficult.

It’s only fairly recently that capacitors have become small and powerful enough to store energy on par with chemical batteries. A few decades ago electrical engineers would prank the new guy by asking them to go into the backroom for a 1 Farad capacitor, which at the time was ludicrous. The poor sap would be back there forever (electrical engineers think they’re so funny). However, that joke has run its course, because today you can buy an over-the-counter, several-thousand Farad capacitor, that’s small enough to fit in your hand (and they pack a punch)!

So, as a general rule of thumb, batteries have a fixed voltage but:

big or new batteries tend to have a low internal resistance, so they can deliver a high current

small or old batteries tend to have a high internal resistance, so they can’t deliver much current

Posted in -- By the Physicist, Engineering, Physics | 32 Comments