Physicist: In quantum mechanics every event is the sum of the possible ways in which that event can happen. Often, events can involve the creation and annihilation of particles. If there are some ways for a thing to happen that involve a certain number of particles, and other ways that involves a different number (or even none), then you can’t really say that the particles were present at all. These “maybe-there” particles are virtual.
Like freaking everything in quantum mechanics, the double slit experiment is a good place to start. In the double slit experiment light is shined onto a pair of slits. The light that gets through is then projected onto a screen. Rather than creating two bright lines (one for each slit) it creates many, which is exactly what you’d expect from a light wave interfering with itself. What’s deeply worrisome about the double slit experiment is that this wave-interference effect continues even when you’re only firing off one photon at a time.
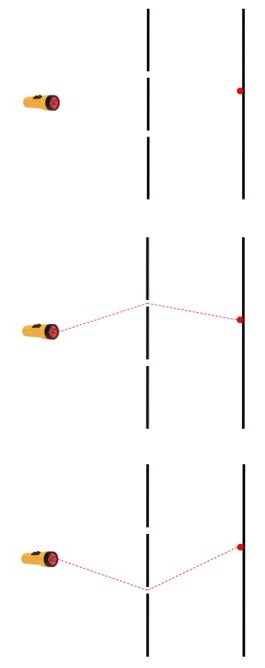
(top) The event is a single photon fired from a light source and detected on the far side of two slits. There are two possible ways this can happen. (middle) the photon goes through the top slit or (bottom) it goes through the bottom slit.
This means that the photon (sorta) passed through both slits, and that to describe the event accurately you need to take into account both possibilities. There have been a lot attempts to get around this weirdness, but none of them have panned out. Physicists always come back to this tremendously bizarre, brain-slapping many-path thing.
For an observer outside of the system (for the moment, don’t worry about what an observer is) the photon is real when it’s emitted by the light source and when it’s detected by hitting the screen. But in between, when it could be taking either path, the question of its realness becomes a little muddled. It’s not “really” on one path or the other, it’s on a combination of both. If it was on only one path we wouldn’t see interference effects, which require more than one path to be taken. Both possible paths are necessary to the event, but neither of them are guaranteed.
This property of light to take every path to a destination isn’t special to light. Everything does it. And it’s not just taking different paths, it’s every possible way for an event to happen; whether that’s particles interacting, or a chemical reaction, or nuclear decay, or whatever. For example, say you fire two electrons at each other, and you want to figure out how they’ll interact (“scatter” off of each other). Similar to the double slit experiment, there are many ways for that to happen and to get an accurate calculation you have to take into account all of those different ways. The two electrons going in, and the two electrons coming out are “real particles” because you can point at them and say “Dudes! Check out this electron!” (or whatever it is that scientists say when they see electrons). Every other particle involved is virtual.
Electrons interact through the electromagnetic force, and that force is basically just a bunch of photons flying back and forth (photons are called the “force carrier” for the EM force). When the electrons get close together they might exchange one photon, or several, or they might exchange them in weird orders, or the same electron might fire off a photon and then absorb it, …
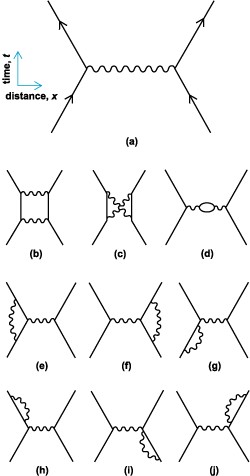
Two electrons scattering off of each other. Even this simple event is the sum of all of these different ways of happening, and infinitely more. The solid lines are the paths of the electrons, and the squiggly lines are the paths of photons.
In every possible way that the electrons might interact, they do, just like the photons in the double slit experiment take every possible path to the screen. Some of these interactions involve lots of photons, or few, or even other particles. For example, in the picture above (d) involves the creation and annihilation of an extra electron/positron pair. If you want to accurately describe how electrons scatter off of each other you need to take into account the possibility of this pair showing up in the middle of the action, or even many pairs. Since this menagerie of particles are all necessary to the interaction, but none of them are guaranteed to exist, physicists have deemed them to be “virtual particles”.
The list of possibilities in the picture is a long way from exhaustive, but in general the more complex the diagram, the less that particular possibility will add to the overall event.
By the way, this is why it’s been such a colossal pain to hunt down the Higgs boson. It shows up as an intermediate particle in some of the ways an interaction can take place, but not all. So far, it’s always been a virtual particle (it’s unlikely to ever be directly observed). So, detecting the Higgs boson, which is involved in just some of the possible ways for particles to interact, is a little like detecting a tiny slit off to the side of the double slit experiment by carefully (very carefully) looking at the interference patterns on the screen.
Whether a particle is real or virtual is kinda a matter of perspective, and this is where the question of what an observer is becomes an issue. A virtual particle is, by definition, a particle that’s involved in an intermediate stage of an event, but that doesn’t interact with the “outside world”. So (and most particle physicists would be a little uncomfortable with this generalization) the photon on its way to the screen, as it takes both paths, is virtual. But, when it hits the screen we can point at it excitedly and say definitively where it is. But we could very easily have put a detector in one of the paths. In so doing we can determine which path the photon is taking, and suddenly it isn’t virtual anymore.
Once again, the Many Worlds interpretation gives us an out. Even if you put a detector in one of the paths, so that the photons are no longer virtual for you, a really distant observer incapable of seeing you, or what you see, would still perceive the whole system (the photon, the slits, the detector, and everything involved) as being in multiple states and so the photon would still be a virtual particle for them.
Point of fact, the various versions of you would also be virtual to such an observer. But, lest you feel unimportant, their various versions would probably be virtual to you as well.