Q: What are virtual particles?

Posted on August 24, 2012 by The Physicist

Physicist: In quantum mechanics every event is the sum of the possible ways in which that event can happen.  Often, events can involve the creation and annihilation of particles.  If there are some ways for a thing to happen that involve a certain number of particles, and other ways that involves a different number (or even none), then you can’t really say that the particles were present at all.  These “maybe-there” particles are virtual.

Like freaking everything in quantum mechanics, the double slit experiment is a good place to start.  In the double slit experiment light is shined onto a pair of slits.  The light that gets through is then projected onto a screen.  Rather than creating two bright lines (one for each slit) it creates many, which is exactly what you’d expect from a light wave interfering with itself.  What’s deeply worrisome about the double slit experiment is that this wave-interference effect continues even when you’re only firing off one photon at a time.

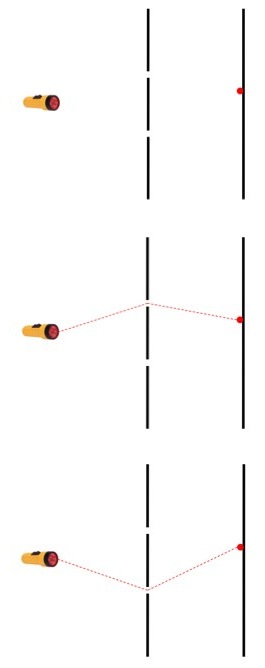
(top) The event is a single photon fired from a light source and detected on the far side of two slits. There are two possible ways this can happen. (middle) the photon goes through the top slit or (bottom) it goes through the bottom slit.

This means that the photon (sorta) passed through both slits, and that to describe the event accurately you need to take into account both possibilities.  There have been a lot attempts to get around this weirdness, but none of them have panned out.  Physicists always come back to this tremendously bizarre, brain-slapping many-path thing.

For an observer outside of the system (for the moment, don’t worry about what an observer is) the photon is real when it’s emitted by the light source and when it’s detected by hitting the screen.  But in between, when it could be taking either path, the question of its realness becomes a little muddled.  It’s not “really” on one path or the other, it’s on a combination of both.  If it was on only one path we wouldn’t see interference effects, which require more than one path to be taken.  Both possible paths are necessary to the event, but neither of them are guaranteed.

This property of light to take every path to a destination isn’t special to light.  Everything does it.  And it’s not just taking different paths, it’s every possible way for an event to happen; whether that’s particles interacting, or a chemical reaction, or nuclear decay, or whatever.  For example, say you fire two electrons at each other, and you want to figure out how they’ll interact (“scatter” off of each other).  Similar to the double slit experiment, there are many ways for that to happen and to get an accurate calculation you have to take into account all of those different ways.  The two electrons going in, and the two electrons coming out are “real particles” because you can point at them and say “Dudes!  Check out this electron!” (or whatever it is that scientists say when they see electrons).  Every other particle involved is virtual.

Electrons interact through the electromagnetic force, and that force is basically just a bunch of photons flying back and forth (photons are called the “force carrier” for the EM force).  When the electrons get close together they might exchange one photon, or several, or they might exchange them in weird orders, or the same electron might fire off a photon and then absorb it, …

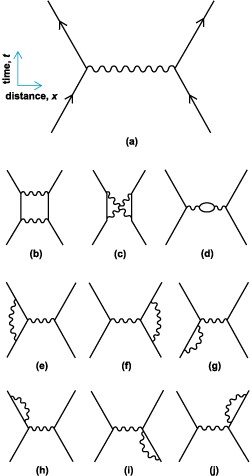
Two electrons scattering off of each other.  Even this simple event is the sum of all of these different ways of happening, and infinitely more.  The solid lines are the paths of the electrons, and the squiggly lines are the paths of photons.

In every possible way that the electrons might interact, they do, just like the photons in the double slit experiment take every possible path to the screen.  Some of these interactions involve lots of photons, or few, or even other particles.  For example, in the picture above (d) involves the creation and annihilation of an extra electron/positron pair.  If you want to accurately describe how electrons scatter off of each other you need to take into account the possibility of this pair showing up in the middle of the action, or even many pairs.  Since this menagerie of particles are all necessary to the interaction, but none of them are guaranteed to exist, physicists have deemed them to be “virtual particles”.

The list of possibilities in the picture is a long way from exhaustive, but in general the more complex the diagram, the less that particular possibility will add to the overall event.

By the way, this is why it’s been such a colossal pain to hunt down the Higgs boson.  It shows up as an intermediate particle in some of the ways an interaction can take place, but not all.  So far, it’s always been a virtual particle (it’s unlikely to ever be directly observed).  So, detecting the Higgs boson, which is involved in just some of the possible ways for particles to interact, is a little like detecting a tiny slit off to the side of the double slit experiment by carefully (very carefully) looking at the interference patterns on the screen.

Whether a particle is real or virtual is kinda a matter of perspective, and this is where the question of what an observer is becomes an issue.  A virtual particle is, by definition, a particle that’s involved in an intermediate stage of an event, but that doesn’t interact with the “outside world”.  So (and most particle physicists would be a little uncomfortable with this generalization) the photon on its way to the screen, as it takes both paths, is virtual.  But, when it hits the screen we can point at it excitedly and say definitively where it is.  But we could very easily have put a detector in one of the paths.  In so doing we can determine which path the photon is taking, and suddenly it isn’t virtual anymore.

Once again, the Many Worlds interpretation gives us an out.  Even if you put a detector in one of the paths, so that the photons are no longer virtual for you, a really distant observer incapable of seeing you, or what you see, would still perceive the whole system (the photon, the slits, the detector, and everything involved) as being in multiple states and so the photon would still be a virtual particle for them.

Point of fact, the various versions of you would also be virtual to such an observer.  But, lest you feel unimportant, their various versions would probably be virtual to you as well.

Posted in -- By the Physicist, Particle Physics, Physics, Quantum Theory | 8 Comments

Q: Would it be possible to create an antimatter weapon by “harvesting” enough antimatter, containing it in an electro-magnetic field and placing that in a projectile?

Posted on August 19, 2012 by The Physicist

Physicist: Yes, but it wouldn’t be easy.

Anti-matter is generated one particle at a time, randomly, during high-energy collisions.  These collisions produce all kinds of particles, including a lot of light (which is just wasted energy).  But if you want to collect anti-matter, what you’re looking for is anti-protons and anti-electrons (also called “positrons”).

High-energy collisions create sprays of random particles (both matter and anti-matter) with random speeds and directions.

Anti-matter can be gathered, but it’s very slow going (only a handful of particles can be created and gathered at a time).  And, of course, you can’t just put it in a mason jar.  Anti-matter annihilates when it touches any kind of matter at all, so it needs to be stored in an absolute vacuum and suspended away from the walls of the container using the only forces we have access to; electric and magnetic.

The anti-matter created and used in some particle accelerators can be contained using “magnetic bottles” which unfortunately only work with charged particles.  If you’ve got just a few charged particles in a bottle then they won’t repel each other too much, but if you get too many they’ll eventually overwhelm the containing magnetic field.  So, keeping a cloud of completely ionized anti-protons around is pretty out of the question.  To neutralize them they can be combined with anti-electrons to create neutral anti-hydrogen.  This is easy enough, however once anti-matter (or any kind of matter) is electrically neutral it tends to fall out of the field that’s holding it, and annihilates when it hits the bottom of the containing vessel.

Neutral matter is normally very difficult to keep suspended in a magnetic field.  There are a relatively few elements that respond well to magnetic fields, such as iron and cobalt, but most materials barely react to magnets at all.  The reaction that normal materials do have is pretty much just a reorientation of their individual electrons, which is generally a very small effect.  It takes a surprisingly powerful magnetic field to get an ordinary material to budge.

Liquid hydrogen (and also liquid anti-hydrogen) is a little bit paramagnetic, so you might be able to keep it suspended in a carefully controlled magnetic field.  However, there are plenty of engineering difficulties.

Water, which is diamagnetic, being suspended in a sufficiently strong magnetic field of about 10 Tesla.

You’d need an very strong magnetic field, and you’d need to keep the hydrogen close to absolute zero to keep it liquid in a vacuum.

Ideally, you’d like something like anti-iron, which is pretty easy to keep suspended and doesn’t require any special preparation (other than the vacuum), instead of anti-hydrogen.  However, getting elements other than hydrogen always involves fusion, which is notoriously difficult to control; we can make fusion bombs, but not fusion power-plants.  With anti-matter, not only does the reaction have to be controlled, but it has to be executed entirely without touching the anti-matter at any time.  So, best to stick with just the anti-hydrogen.

Anti-matter (anti-hydrogen in particular) requires a hell of a lot of energy to maintain the magnetic fields, and a really good vacuum pump.  Anti-matter is really dangerous stuff to keep around.  The only other stuff that comes close to creating the kind of bang that anti-matter can create is nuclear weapons, but if you leave a nuke on a shelf for too long it becomes inert (safe), while anti-matter never loses its punch (dangerous).  On the other hand, while a nuclear weapon is very difficult to set off correctly, there is no wrong way to set off anti-matter.  The most powerful nuclear weapon ever set off weighed about 30 tons and released about as much energy as a 1 kg chunk of anti-matter.

Despite a “glowing” recommendation like that, in terms of efficiency you get a much better return from fissionable materials (nuclear weapons), considering that you can just dig up the material and then release its energy.  All anti-matter is the result of highly inefficient direct energy-t0-matter conversion.  The total energy released by an anti-matter bomb is always substantially less than the total amount of energy that went into the production.

But, long story short; anti-matter weapons are possible, but not practical.

The water droplet photo is from here.

Posted in -- By the Physicist, Physics | 11 Comments

Q: If Earth was flat, would there be a horizon? If so, what would it look like? If the Earth was flat and had infinite area, would that change the answer?

Posted on August 14, 2012 by The Physicist

Physicist: There’d definitely still be a horizon if the Earth were flat.  It would be in almost exactly the same place, and look essentially identical.  While the Earth isn’t flat, adherents to that theory are correct in that it’s nearly so, and if you’re standing on the surface of a round something the size of the Earth it’s difficult to tell the difference (in fact, mathematically you can make the argument that a flat Earth acts the same as an infinitely big Earth).

Who would even notice?

For someone around 5’6″ tall, if the Earth were perfectly flat the horizon would be about 0.04° higher.  That’s about the width of a (mechanical) pencil lead held at arm’s length.  Unless you have short arms, in which case you’ll need to shave down the lead a little.

Even if the Earth were perfectly flat and went on forever, the horizon would still be exactly level: 180° of sky and 180° of ground (instead of the paltry 179.92° of ground we have).  The only difference between a finite flat Earth and an infinite flat Earth is that no matter how tall you are on an infinite flat Earth, the horizon always stays in the same place.

However, even though the horizon of an infinite and flat Earth might actually be in the same place, it wouldn’t appear to be.  An infinite plane has an extremely simple gravitational field; uniform and exactly the same regardless of distance.  Normally the higher you are the weaker the gravity, but for a flat Earth that isn’t the case.

As such, light, which drops only imperceptibly under Earth’s gravity, has an infinitely great distance over which to do its dropping.  The effect would require tremendous distances (as in; interstellar distances), but if you’ve got an infinite plane, that kind of distance is cheap.

Given enough time and distance light will eventually curve back toward an infinite plane of matter. So if you’re standing somewhere on the surface and you look up you’ll see light that started somewhere else on the surface.  Instead of a horizon, the world would look like it rises up on all sides and encloses you.

When you look up from what should be the horizon you’ll just see more of the infinite-flat-Earth.  The one exception is what you’d see if you looked straight up.  Directly above you you’d find the entire horizon bunched up at that point.

Answer gravy: It’s not interesting enough to include in the post directly, but here’s how the math above was done:

If you’re standing on a sphere with radius R and you’re H tall, then the distance from your head to the middle of the sphere is R+H.  Your line of sight to the horizon is a tangent line to the sphere.  This allows you to draw a right triangle and do a little trigonometry.

θ is the angle between the “true horizon” and the perfectly level “ideal horizon”.  Coincidentally, it’s also the angle between where you’re standing on a sphere and the farthest thing you can see on the surface.

So, \cos{(\theta)} = \frac{R}{R+H} and \theta = \arccos{\left(\frac{R}{R+H}\right)}.  Plug in R = 6,378,100 meters and H = 1.68 meters (which is 5’6″), and you find that θ = 0.04°.

By the end of college, electrical engineers and physicists get sick to death of the example of the infinite plane of anything (be it matter, electrical charge, kittens, whatnot).  The reason an infinite plane is useful is that it has some nice symmetry.  You can argue that, since no direction is special (by being close to an edge for example) gravity always points straight into or out of the plane-o-stuff.  Symmetry is useful when you use a Gaussian surface, because you can ignore buckets of math.

Basically, draw a “bubble” around a lump of matter.  The total gravitational field pointing through that bubble will be proportional to the amount of matter inside.  So, the more matter, the more gravity.  The bigger the bubble, the less the strength of the field through any particular part of the surface (by the by, there’s an example of this in action here).  If the Gaussian surface you choose is a rectangular box that punches through the flat-Earth, then you find that it doesn’t matter how tall the box is.

The total amount of gravity pointing into any imaginary box you can draw is always proportional to the amount of matter in that box. In this case, no gravity points through the sides (by symmetry) so it all points through the top. But if you make the box taller that doesn’t change. As a result, for an infinite plane gravity stays the same forever. QED y’all!

Uniform and infinite sheets of matter or charge have gravitational or electric fields that extend, without changing, forever.  Of course, there are barely any infinite planes of stuff out there, so this isn’t a situation that ever actually comes up.  However!  If you’re close enough to a surface it can seem to be nearly infinite, so the infinite-plane solutions are often good enough.

And often as not, “good enough” is good enough for physics.

Posted in -- By the Physicist, Geometry, Physics | 73 Comments

Q: Is there an experiment which could provide conclusive evidence for either the Many Worlds or Copenhagen interpretations of quantum physics?

Posted on August 9, 2012 by The Physicist

Physicist: Probably not.

Tiny things don’t act the way they should.  You got super-positions, wave-like behavior, action at a distance, quantum tunneling, quantum teleportation, interaction-free detection, all kinds of things that should be impossible or paradoxical but aren’t.  The laws of the very small (quantum mechanics) work well on their own, and the laws of the large (classical physics) work well on their own as well.  The difficulties (and most of that long list of weird effects) come from the interplay between the big and small laws.  For example, in quantum mechanics things can be in multiple locations, but in classical physics they clearly can’t.  When something in multiple places (small rules) is detected by some kind of detector, it’s always found to be in one place (large rules).  The Copenhagen and Many Worlds (MWI) interpretations are attempts to explain why there seem to be different, contradictory rules for large and small scales.

The Copenhagen interpretation basically says “large/complex things are always in one state, don’t obey quantum mechanical laws, and *something* happens when small quantum mechanical systems interact with larger systems that forces them to be in one state as well”.  Copenhagen comes in a lot of flavors; consciousness-based (which can come with a side of Chopra or Secret), size-based, complexity-based, random collapse, and so on.  The most common form of Copenhagen (in non-spiritual circles) is a size and/or complexity type: for some reason, when things become large enough, or interact with things that are large enough, they stop behaving quantum mechanically.

The advantage is “somehow” is a pretty safe thing to say, and (as long as you don’t look at the details) Copenhagen is also the simplest interpretation.  However, there’s no end to the variety of contradictions and paradoxes it creates.  If you’ve ever heard of a quantum mechanical paradox: that’s one.

The Many Worlds interpretation makes a different safe, but weird, statement, “quantum mechanical laws, all of them, work all the time at every level and the large-scale, classical world we see is actually a result of those laws”.  MWI also comes in a few flavors, but the “keep using the same laws” version is the simplest to say, and most difficult to understand.  The exact reasons behind why quantum mechanics leads to a classical world are subtle and math-heavy.  In quantum mechanics not only can individual particles be in multiple states, but so can groups of particles, and even systems of arbitrarily great size and complexity.

The advantage is that all of those paradoxes that come from trying to reconcile two different kinds of physics (quantum vs. classical) disappear.  On the other hand, when you try to describe some of the repercussions you’ll sound balls-out crazy.  The same “many-stateness” that shows up for individual particles and tiny systems shows up for everything including people, puppies, countries, solar systems, freaking everything.  In exactly the same way that a single photon can pass through two slits, or otherwise be in a tremendous number of states, a person can live an arbitrarily large number of different lives all at once (the different versions are “unaware” of each other in both cases).  Each of those different versions experiences a different classical (seemingly non-quantumy) world.

Unfortunately, both MWI and Copenhagen predict that the world of the small and the world of the large will behave differently (or at least will appear to behave differently).  So (to finally answer the original question) the two interpretations differ in their experimental predictions only for larger systems.  While MWI says that things will continue to obey quantum mechanical laws forever, Copenhagen says that at some point between the atomic scale and the every-day scale a system will have to obey only classical laws.

Back in the day, when these two interpretations were first conceived, the only things that had demonstrated super-position were individual particles.  However, since then intrepid, handsome/beautiful physicists have managed to demonstrate the same quantumy properties in progressively larger things, including buckyballs and even a metal, 30 μm long needle large enough to be seen with the naked (squinting) eye.

Buckminsterfullerene and, at about 50,000 times larger, a needle. Both have been shown to exhibit forms super-position, a purely quantum effect that is classically impossible.

Every experiment that can be done, so far, has returned a positive result for the quantum nature of things, and pushed back the “Copenhagen scale” at which classical physics must take over.  Considering that the scale at which Copenhagen would have to kick in keeps getting larger and larger, it seems like MWI is the better choice.  The goal posts to disprove Copenhagen get moved farther and farther back by fancier and better controlled experiments.  Copenhagen is fast becoming a “theory of the gaps“.

A really, completely, absolutely definitive experiment would need to demonstrate some form of super-position with an object as big as (or involving) a person.  However, the larger something is, the more difficult it is to detect its quantum nature, and the more carefully controlled the experiment must be.  Ideally, putting someone in a box, demonstrating that that person can behave in a “many-state-kind-of-way”, and then bringing them out would put the debate to rest.  Unfortunately, for a number of reasons, this experiment is very unlikely to ever be done.

Posted in -- By the Physicist, Experiments, Philosophical, Physics, Quantum Theory | 7 Comments

Q: If you could drill a tunnel through the whole planet and then jumped down this tunnel, how would you fall?

Posted on August 3, 2012 by The Physicist

Physicist: This is a beautiful question, in a small part because it’s an interesting thought experiment with some clever math, but mostly because of all the reasons it couldn’t be done and wouldn’t work.  Right off the bat; clearly a hole can’t be drilled through the Earth.  By the time you’ve gotten no more than 30 miles down (less than 0.4% of the way through) you’ll find your tunnel filling will magma, which tends to gunk up drill bits (also melt everything).

Jumping into a hole drilled through the Earth. What’s the worst that could happen?

But!  Assuming that wasn’t an issue, and you’ve got a tube through the Earth (made of unobtainium or something), you still have to contend with the air in the tube.  In addition to air-resistance, which on its own would drag you to a stop near the core, just having air in the tube would be really really fatal.  The lower you are, the more air is above you, and the higher the pressure.  The highest air pressure we see on the surface of the Earth is a little under 16 psi.  But keep in mind that we only have about 100 km of real atmosphere above us, and most of that is pretty thin.  If the air in the tube were to increase in pressure and temperature the way the atmosphere does, then you’d only have to drop around 50 km before the pressure in the tube was as high as the bottom of the ocean.

Even worse, a big pile of air (like the atmosphere) is hotter at the bottom than at the top (hence all the snow on top of mountains).  Temperature varies by about 10°C per km or 30 °F per mile.  So, by the time you’ve fallen about 20 miles you’re really on fire a lot.  After a few hundred miles (still a long way from the core) you can expect the air to be a ludicrously hot sorta-gas-sorta-fluid, eventually becoming a solid plug.

But!  Assuming that there’s no air in the tube, you’re still in trouble.  If the Earth is rotating, then in short order you’d be ground against the walls of the tunnel, and would either be pulverized or would slow down and slide to rest near the center of the Earth.  This is an effect of “coriolis forces” which show up whenever you try to describe things moving around on spinning things (like planets).  To describe it accurately requires the use of angular momentum, but you can picture it pretty well in terms of “higher things move faster”.  Because the Earth is turning, how fast you’re moving is proportional to your altitude.  Normally this isn’t noticeable.  For example, the top of a ten story building is moving about 0.001 mph faster than the ground (ever notice that?), so an object nudged off of the roof can expect to land about 1 millimeter off-target.  But over large changes in altitude (and falling through the Earth counts) the effect is very noticeable: about halfway to the center of the Earth you’ll find that you’re moving sideways about 1,500 mph faster than the walls of your tube, which is unhealthy.

The farther from the center you are, the faster you’re moving.

But!  Assuming that you’ve got some kind of a super-tube, that the inside of that tube is a vacuum, and that the Earth isn’t turning (and that there’s nothing else to worry about, like building up static electricity or some other unforeseen problem), then you would be free to fall all the way to the far side of the Earth.  Once you got there, you would fall right through the Earth again, oscillating back and forth sinusoidally exactly like a bouncing spring or a clock pendulum.  It would take you about 42 minutes to make the trip from one side of the Earth to the other.

The clever math behind calculating how an object would fall through the Earth:  As you fall all of the layers farther from the center than you cancel out, so you always seem to be falling as though you were on the the surface of a shrinking planet.

What follows is interesting mostly to physics/engineering majors and to almost no one else.

It turns out that spherically symmetric things, which includes things like the Earth, have a cute property: the gravity at any point only depends on the amount of matter below you, and not at all on the amount of matter above you.  There are a couple of ways to show this, but since it was done before (with pictures!), take it as read.  So, as you fall in all of the layers above you can be ignored (as far as gravity is concerned), and it “feels” as though you’re always falling right next to the surface of a progressively smaller and smaller planet.  This, by the way, is just another reason why the exact center of the Earth is in free-fall.

The force of gravity is F = -\frac{GMm}{r^2}, where M is the big mass, and m is the smaller, falling mass.  But, since you only have to consider the mass below you, then if the Earth has a fixed density (it doesn’t, but if it did) then you could say M = \rho \frac{4}{3}\pi r^3, where ρ is the density.  So, as you’re falling F = -\left(\frac{Gm}{r^2}\right)\left(\rho \frac{4}{3}\pi r^3\right) = -\left(\frac{4}{3}G\rho \pi\right) mr.

Holy crap!  This is the (in)famous spring equation, F = – kx!  Physicists get very excited when they see this because it’s one of, like, 3 questions that can be exactly answered (seriously).  In this case that answer is r(t) = R\cos{\left(t\sqrt{\frac{4}{3}G\rho \pi} \right)}, where R is the radius of the Earth, and t is how long you’ve been falling.  Cosine, it’s worth pointing out, is sinusoidal.

Interesting fun-fact: the time it takes to oscillate back-and-forth through a planet is dependent only on the density of that planet and not on the size!

Posted in -- By the Physicist, Brain Teaser, Physics | 102 Comments

Q: How many people riding bicycle generators would be needed, in an 8-hour working day, to equal or surpass the energy generated by an average nuclear power plant?

Posted on July 29, 2012 by The Physicist

Physicist: A person on a bike can optimistically generate around 200 watts, and an average nuclear power plant generates 800 MW of power (although a big nuclear power plant generates many times more power than a small one).

The power plant of the future?

Given those two “statistics”, it would take somewhere around 12 million people on bicycles for eight hours to equal the power output of a single nuclear power plant for a day.  Based on schematics for Viking longships, which were essentially mobile motivation machines, we can reasonably say that a “spin class power plant” would take up about 6.5 square miles (not including walkways or bathrooms) and require about 300,000 task-masters to keep the power supply steady.  This, it’s worth noting, exceeds the total number of taskmasters currently living in Norway (oppgave mestere i Norge unite!).

Taskmaster and plutonium pellet.  In their natural states, the taskmaster is perpetually cold and the pellet is perpetually hot.

The take home point is: nuclear energy doesn’t mess around.  Other than extension cords (a technology still in its infancy), there really aren’t any other ways to, for example, power a spacecraft on a 50 year mission beyond the solar system, or to run a submarine for a few decades without refueling, on nothing more than a bucket-full of fuel.

The power plant picture is from here, and the taskmaster is really Ivar the Boneless from Erik the Viking.

Posted in -- By the Physicist, Engineering | 2 Comments