Q: How can we see the early universe and the Big Bang? Shouldn’t the light have already passed us?

Posted on June 25, 2012 by The Physicist

Physicist: This is a very common question that’s generated (as best I can tell) by a misrepresentation of the Big Bang that you’ll often see repeated in popular media.  In the same documentary you may hear statements along the lines of:

“our telescopes can see the light from the earliest moments of the universe” and

“in the Big Bang, all of the energy and matter in the universe suddenly exploded out of a point smaller than the head of a pin”.

The first statement is pretty solid.  Technically, the oldest light we can see is from about 300,000 years after the Big Bang, but we can use it to infer some interesting things about what was happening within the first second (which is the next best thing to actually being able to see the first second).  That light is now the Microwave Background Radiation.

The second statement has a mess of holes in it.

First, when someone says that all of the matter and energy in the universe was in a region smaller than the head of a pin, what they’re actually talking about is the observable universe, which is just all of the galaxies and whatnot that we can see.  If you’re standing on the sidewalk somewhere you can talk meaningfully about the “observable Earth” (everything you can see around you), but it’s important to keep in mind that there’s very little you can say about the size and nature of the entire Earth from one tiny corner of it.

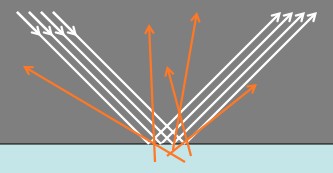
The second statement also implies that there’s time and space independent of the universe.  Phrases like “suddenly exploded out of a point” makes it sound like you could have been floating around, biding your time playing solitaire and checking email in a vast void, and then Boom! (pardon; “Bang!”) a whole lot of stuff suddenly appears nearby and expands.  If the Big Bang and the expansion of the universe were as straightforward as an explosion and things flying away from that explosion, then the earliest light would be on the front of our ever-expanding universe.  If that were the case (and it seems to be from the images and videos presented in, like, every documentary evar), then there’s no way you’d be able to see the light from the early universe.

The incorrect misrepresentation often shown (implied) in many science shows and books: the Big Bang as an explosion that happens at some point, and all of the resulting light (blue ring) and matter (stuff in the ring) in the universe spreading out from that point (red star).  However, this means that the light from the early universe would be long gone, and we would have no way to see it.

Just to be doubly clear, the idea of the universe exploding out of one particular place, and then all of the matter flying apart into some kind of pre-existing space, is not what’s actually going on.  It’s just that getting art directors to be accurate in a science documentary is about as difficult as getting penguins to walk with decorum.

The view of the universe that physicists work with today involves space itself expanding, as opposed to things in space flying apart.  Think of the universe as an infinite rubber sheet*.  The early universe was very dense, and very hot, what with things being crammed together.  Hot things make lots of light, and the early universe was extremely hot everywhere, so there would have been plenty of light everywhere, shooting in every direction.

If you start with light everywhere, you’ll continue to have it everywhere.  The only thing that changes with time is how old the light you see is, and how far it’s traveled.  The expansion of the universe is independent of that.  Imagine standing in a huge (infinite) crowd of people.  If everyone yelled “woo!” (or something equally pithy) all at once, you wouldn’t hear it all at once, you’d hear it forever, from progressively farther and farther away.

Everyone in a crowd yells “woo!” at the same time. As time marches forward you (blue dot) will continue to hear the sound, but the sound you’re hearing is older and from farther away (red line). Light from the early universe works the same way.

As the universe expands (as the rubber sheet is stretched) everything cools off, and the universe becomes clear, as everything is given a chance to move apart.  That same light is still around, it’s still everywhere, and it’s still shooting in every direction.  Wait a few billion years (14 or so), and you’ve got galaxies, sweaters for dogs, hip-hop music; a thoroughly modern universe.  That old light will still be everywhere, shooting in every direction.  Certainly, there’s a little less because it’s constantly running into things, but the universe is, to a reasonable approximation, empty.  So most of the light is still around.

The expansion of the universe does have some important effects, of course.  The light that we see today as the cosmic microwave background started out as gamma rays, being radiated from the omnipresent, ultra-hot gases of the young universe, but they got stretch out, along with the space they’ve been moving through.  The longer the wavelength, the lower the energy.  The background energy is now so low that you can be exposed to the sky without being killed instantly.  In fact, the night sky today radiates energy at the same intensity as anything chilled to about -270 °C (That’s why it’s cold at night!  Mystery solved!).  Even more exciting, the expansion means that the sources of the light we see today are now farther away than they were when the light was emitted.  So, while the oldest light is only about 14 billion years old (and has traveled only 14 billion light years), the location from which it was emitted can be calculated to be about 46 billion light years away right now!

Isn’t that weird?

*The universe may be “closed”, in which case it’s curved and finite (like the surface of a balloon),  or “open”, in which case it’s flat and infinite in all directions (like an infinite rubber sheet).  “Curved” and “flat” are a little hard to picture when you’re talking about 3 dimensional space, but there’s a little help here.  So far, all indications are that the universe is flat, so it’s either infinite or so big that the curvature can’t be detected by our equipment (kinda like how the curvature of the Earth can’t be detected by just looking around, because the Earth is so big).  In either case, the expansion works the same way.  However, in the open case it’s a touch more difficult to picture how the Big Bang worked.  The universe would have started infinite, and then gotten bigger.  The math behind that is pretty easy to deal with, but it’s still harder to imagine.

Posted in -- By the Physicist, Astronomy, Physics | 48 Comments

Q: Are beautiful, elegant or simple equations more likely to be true?

Posted on June 20, 2012 by The Mathematician

Mathematician:

It is not uncommon to hear physicists or mathematicians talk about the beauty, simplicity or elegance of equations or theorems, and even claim that they are sometimes led to a correct formula (or away from an incorrect one) by considering what is simple or elegant. Consider, for example, the words of the Nobel prize-winning physicist Murray Gell-Mann:

“Three or four of us in 1957 put forward a partially complete theory of the weak [nuclear] force, in disagreement with the results of seven experiments. It was beautiful and so we dared to publish it, believing that all those experiments must be wrong. In fact, they were all wrong.”

and Albert Einstein’s remark:

“I have deep faith that the principle of the universe will be beautiful and simple.”

Could there be something to these remarkable claims? Is beauty in physics evidence for some kind of “intelligent” universe, or are there more mundane explanations? Is elegance in mathematics evidence for an underlying structure to reality? Or can this be explained away by psychological or practical considerations?

To begin answering these questions, an important thing to notice about the aesthetics of equations is that what appears to be simple or elegant may sometimes only be so because of the way that symbols are defined. For example, consider the remarkable and rather minimalist “heat equation”

\Delta f = f '

which, when solved for the function f with a given condition on its boundary, will describe how heat would actually flow over time on a specified surface. Is it not astounding that we can describe such a powerful physical law with just 5 symbols?

A deeper look at this equation shows us that the apparent simplicity here is in part an illusion. First of all \Delta, which is known in this context as the Laplace operator, can be thought of as simply a short hand notation. If we replace \Delta f and f' with their respective definitions, we are left with the markedly less simple looking equation:

\Large \frac{d^2 f}{dx^2} + \frac{d^2 f}{dy^2} + \frac{d^2 f}{dz^2} = \frac{d f}{dt}

Derivative operations (which are taken a total of seven times in the above equation) are not themselves trivial operations, and are typically defined via a limiting procedure. If we are crazy enough to replace all the derivative operations with their definitions, we are left with an equation which is just plain long and ugly, even after performing some simplification:

\lim_{h \to 0} \frac{1}{h^2} (3 f(x,y,z,t) + f(x+2h,y,z,t) - 2 f(x+h,y,z,t) + f(x,y+2h,z,t) - 2 f(x,y+h,z,t) +f(x,y,z+2h,t) - 2 f(x,y,z+h,t) ) ) = \lim_{h \to 0} \frac{1}{h} (f(x,t+h) - f(x,t))

The point to realize here is that mathematicians and physicists make very careful choices when selecting their notation to vastly compress very complicated ideas. You can make anything look simple by giving it a unique symbol, and you can make anything look complicated by recursively expanding the definitions it relies on. Even references to the number 1 look extremely complex if you replace them using a formula like:

1 = \sum_{k=0}^{\infty} (\frac{\pi}{2})^{2k+3-2} \frac{(2-3)^k }{(2k+3-2)!}

Doing so would not change what’s true, but it sure would confuse a lot of people and make formulas much harder to work with.

To make their notations as useful as possible, physicists and mathematicians typically define symbols in such a way as to make important formulas easy to write down and manipulate. The reason that the Laplace operator \Delta gets its own symbol is because it’s so damn important. So important theorems and known physical laws may have some tendency to seem simpler than they are when the equations are written out, because the choice of symbols was made, in part, to make them easy to write out.

All of this being said, notation is not the end of the story on whether elegance or simplicity relates to truth in math in physics. Another important point to consider is that in many cases a single physical law can cause a multitude of different effects which may not, at first, seem to be related. To give some classic examples, before Newton’s era it was not at all obvious that the force that causes us to fall to the ground when we jump is the same force that keeps planets in orbit in our solar system. Likewise, before the 1800’s it was not known that electric fields, magnetic fields and light are manifestations of a single phenomena now known as electromagnetism. Similarly, before the era of Einstein it was not understood that conservation of energy and conservation of momentum could be thought of as effectively being part of a single conservation law.

There are some cases in physics where simpler and more elegant theories have won out over more complex theories because they correctly identify seemingly unrelated phenomena as having a single cause. Theories which treat inherently connected ideas as being wholly different are destined to be replaced since their lack of unification creates redundancy and therefore unnecessary complexity in the theory. This is one important reason why ugly, complicated theories can often be outdone by what seem to be more beautiful ones. We find it more beautiful to have one explanation for two results than to have two distinct explanations, and if the results really are just caused by one phenomenon, the single explanation will typically be easier to express and work with mathematically than both of the other two.

Another, related reason why we might expect simplicity to win out over complexity, is because of a rule of thumb known as Occam’s Razor. This idea, in its typical modern form, states that given multiple possible explanations for a phenomena that are otherwise equally plausible, we should prefer the one that is the simplest.

A potential example of Occam’s Razor in practice relates to the Ptolemaic explanation of the motion of the planets, which was the accepted theory in some places for many hundreds of years. The basic idea of this theory was that planetary motion consists of “epicycles” around the fixed planet earth. This means that planets were thought to make circular orbits around earth, but that during these circular orbits the planets orbited in smaller circles along the orbits, and along those smaller circular orbits they orbited in still smaller circles, etc. This model was intrinsically very complex because by adjusting the epicycles so that there were a sufficient number of circular orbits within circular orbits at appropriate speeds, one could have described pretty much any shape of orbit, real or imagined. In other words, the model had a large number of free variables which gave it enormous flexibility and therefore complexity. Copernicus eventually laid the Ptolemaic model to waste by replacing it with a far simpler model with far fewer free parameters, which he accomplished merely by shifting the center of the circular planetary orbits to be the sun rather than the earth. However, the basic form of his new theory still did not agree perfectly with observation, and so required some ad hoc refinements that introduced extra complexity. This further complexity was eventually removed by Kepler who refined the model yet again by allowing for elliptical rather than circular orbits, which now is known to be an excellent explanation for the orbits that are observed. The key difference in these explanations for orbits is that the theory of epicycles is complex enough to explain almost any conceivable orbit you could ever think of, whereas Kepler’s idea of elliptical orbits with the sun at one focus of the ellipses was just complex enough to explain what was actually observed but without being complex enough to explain the universe had we observed substantively different orbits than actually exist. In other words, Kepler’s theory is as complicated as it needs to be to explain reality.

There does seem to be something to this Occam’s Razor business. It certainly seems to be a bad idea to add extra assumptions to a theory if those new assumptions don’t improve explanatory power, and it also seems like a bad idea to use a theory that’s so complex (or has so many variables that can be tweaked) that it can explain pretty much any experimental result you might get. There is even some neat mathematical theory which shows that taking an Occam’s Razor like approach is a good idea in certain contexts (see, for instance, the work on Solomonoff Induction and the Ockham Efficiency Theorem). But we’re a long way off from being able to formally prove that we should use Occam’s Razor as a general rule of thumb. In fact, we don’t even know what the right notion of “simpler” is to use in real world problems when we claim that “simpler explanations are more likely to be true.”

There are a few more points about the relationship between beauty and truth in physics and math that I feel are worth mentioning. To begin with, as physicist Murray Gell-Mann (quoted above) mentions in his TED talk on beauty and truth in physics, symmetry plays a key role in simplicity. For example, since all the known laws of physics treat the three dimensions of space equally, we can often greatly simplify equations by writing expressions such as

\nabla f

(which is the gradient of f, which constructs a vector of the derivatives of f with respect to each of its variables) rather than having to write an equivalent but much more cumbersome set of equations where we treat each dimension of space separately, as in:

\frac{df}{dx} \frac{df}{dy} \frac{df}{dz}

The point here is that symmetry makes it easier to simplify equations. Of course, this argument goes beyond just the symmetry of the three dimensions of space, and applies also to symmetry in time, rotation, etc.

Another idea that should be mentioned is that typically mathematical expressions have a number of equivalent forms. For example, we could define the exponential function e^x using any of the following nearly interchangeable definitions:

f(x) = \lim_{h \to \infty} (1 + \frac{x}{h})^h f(x) = f'(x), f(0) = 1 f(x) = \sum_{k=0}^{\infty} \frac{x^k}{k!} f(\ln(x)) = x f(x+y) = f(x) f(y), f(1) = e f(x) = \cosh(x) + \sinh(x)

None of these definitions for e^x is intrinsically best. Mathematicians have the choice to use whichever definition is more useful for any given purpose, and often times it is precisely the simpler or more elegant seeming definitions that are used most commonly because they are easier for us to understand and manipulate.

As a final point, it is worth noting that quite a bit of the more theoretical mathematical work is driven more by the aesthetic and psychological appeal of the theorems than by the importance of those theorems in solving practical problems that arise in the real world. One prime example of this phenomenon is the field of number theory, which while popular and very elegant, found almost no practical applications before it was (unexpectedly) linked to the field of cryptography and secure online banking.

Not only do mathematicians like equations that seem elegant, but it is easier to publish results that strike the reviewers as elegant rather than clumsy and awkward. Keeping these ideas in mind, it is no surprise to find that some of the most researched areas of math even today have great beauty but few real world applications.

In conclusion, the relationship between elegance and truth in physics and math is a complicated one, which relates to practical considerations such as choices for notation and definitions, psychological phenomenon such as the personal preferences and aesthetic sensibilities of the practitioners, and deeper physical or mathematical ideas such as symmetry, the unification of seemingly unrelated results, and Occam’s razor.

Posted in -- By the Mathematician, Equations, Math, Philosophical, Physics | 13 Comments

Q: If quantum mechanics says everything is random, then how can it also be the most accurate theory ever?

Posted on June 15, 2012 by The Physicist

The original questions were:

How can quantum computers actually be more useful if we cannot observe superposition, since trying to harness two states at once would just produce one state?

Quantum Physics … is so full of uncertainty and Einstein didn’t like “God playing dice with the world.” How would you explain that quantum physics has today led to the development of the most accurate theories we have till date?

Physicist: Whether a quantum system is random or not kinda depends on what you’re taking about.  For example, the electrons in an atom show up in “orbitals” that have extremely predictable shapes and energy levels, and yet if you were to measure the location of an electron within that orbital, you’d find that the result is pretty random.

One of the great victories of quantum mechanics was to prove, despite Einstein’s scoff to the contrary, that God does play dice with the world.  Everything in the universe is in multiple states, but when a thing is measured it’s suddenly found to be in only one state (technically; a smaller set of states).  Setting aside what a measurement is and what measurements do, the result of a measurement (the state that a thing will be found in) is often, but not always, fundamentally random and unpredictable.

For example, when a beam of light passes through a beam splitter the beam splits (hence the name) into two beams of half the intensity.  In terms of waves this is pretty easy to explain; some of the wave’s energy goes through, and some reflects off of the splitter.  In quantum theory you continue to describe light (and everything else) as a wave, even when you turn down the light source so low that there’s only one photon passing by at a time.

According to quantum theory (and verified by experiment) there is no way to predict which direction a photon will take through a beam splitter. This situation is "irreducibly random".

So, in exactly the same way that you’d mathematically describe a wave as going through and being reflected, you also describe the photon as both going through and being reflected.  Place a pair of detectors in the two possible paths and you’re making a measurement.  Suddenly, instead of taking both paths at the same time, the photon is found on only one (indicated by which detector detects), and there is absolutely no way to predict which path that will be.

So on the face of it, that seems like it should be the end of the road.  There’s an irreconcilable randomness to the measurements of quantum mechanical systems.  In the example above (and millions of others like it) it is impossible to make an accurate prediction.  But keep in mind; it is possible to be clever.

The quantumy description of each photon going through the beam splitter isn’t a simple as “it’s totally random which path it takes”.  Each photon is described, very specifically and non-randomy, as taking both paths.

By properly adjusting the path lengths you can make it so that all of the photons go to a single detector. You can't predict which path the photon takes, but you can perfectly predict the end result.

Take the same situation, a laser going through a beam splitter, and add a little more to the apparatus.  With a couple mirrors you can bring the two paths back together at another beam splitter.  The light waves from both paths split again at the second beam splitter, but when you’re looking at the intensity of what comes out you have to take into account how the light waves from the two paths interfere.

When waves are combined they don't simply add, they interfere. The sum of two waves can be larger (constructive interference) or smaller (destructive interference) depending on how they line up.

By carefully adjusting the distances you can cause one path to experience complete destructive interference, and the other to experience complete constructive interference.  This is all fine and good for a laser beam, but when you turn down the intensity until there’s only one photon passing through at a time, you still find that (in the example pictured) only the top detector will ever be triggered.  This isn’t “theory” by the way, it’s pretty easy to set this up in a lab.

This is a little spooky, so take a moment.  The quantum theory description is that a single photon will take both paths. If detectors are placed in the two paths it is impossible to predict which will fire.  But if the paths are recombined, we can see that the photon took both paths, because it interferes with itself in a very predictable way, and produces very predictable results.  If, instead, we took the “quantum mechanics says things are random” tack we’d expect that at each beam splitter the photons made a random choice, and the detectors in the second example would each fire half the time.

So quantum theory can predict that an event will be random, or in other situations it can accurately predict the outcome (even though that prediction sometimes seems impossible).  It all comes down to a judicious application of measurements and how you allow the quantum system to interact with itself.

This particular example can be extended to allow for “interaction free measurements“, which seem impossible, but are in fact just another (accurate) prediction of quantum mechanics.  The non-randomness of quantum mechanics is the basis of quantum algorithms, and (in a less direct way) is why chemistry “works”.

Posted in -- By the Physicist, Physics, Quantum Theory | 13 Comments

Q: Why do wet stones look darker, more colorful, and polished?

Posted on June 9, 2012 by The Physicist

Physicist: This is surprisingly subtle!

Dry stones, wet stones, and a polished dry stone.

There are two effects that come into play: the way light reflects off of the surface (surface reflection) and the way light bounces into and then out of the surface (subsurface reflection).

Surface reflection is responsible for the darkening of wet or polished stones.  But rather than actually making the surface darker, what polishing or wetting a surface does is “consolidate” the reflecting light into one direction.

Rough surfaces reflect in many directions, smooth surfaces reflect in one direction.

If the light hitting a patch of surface is scattered, then you’ll see at least a little of it from any angle.  However, if the light only reflects in one direction, then you’re either in the right place to see it or you’re not.  So a polished surface looks darker from most angles, but much brighter from just a few angles.  The bottom stone in the top picture is a good example.

When a thin film of water is added to a stone it creates a new, second surface above the stone’s actual surface.  The surface of the water film reflects in the same way that a polished stone reflects because it’s so smooth.  You’re never going to see water with a “sand-paper rough” surface.  Water makes stones shiny but dark in the same way that lakes and oceans are shiny but dark.

The interesting colors of stones come, for the most part, from subsurface reflection.  That is; light penetrates the surface, wanders around for a little bit, and then pops back out again.

Surface and subsurface reflection (interface and body reflection).

By its nature, subsurface (sometimes called “body”) reflection is a scattering reflection.  While polishing will cause all of the surface reflecting light to go in the same direction, there isn’t much you can do to stop subsurface reflection from scattering.  Different materials absorb light of different colors, and allow others to pass, so light that undergoes subsurface reflection picks up some colors.  Technically; pretty colors.

Surface-reflected light, on the other hand, tends to retain its white, lack of color (here I’m assuming you’re not looking at rocks under a heating lamp or something).  So, normally when you look at a rough stone you’ll be seeing the stone’s color, but it will be “drowned out” by the white light being scattered off of the surface.  With a polished stone, that white light is being reflected away in one direction, so unless you’re in the path of that white light you’ll just be seeing the more colorful subsurface-reflected light.  Polishing doesn’t make a stone more colorful, but it does “turn up the contrast” on the colors already present.

If you’re not in the path of the surface reflected light (white) you’ll only be seeing subsurface reflected light (orange).

In the case of water there’s an added effect.  A thin layer of water actually helps light to penetrate the surface of the stone, which increases subsurface reflection, and adds to the color.

When light moves between materials with different indexes of refraction it can either pass through the boundary or reflect. The smaller the difference in indexes, the less light will reflect.  Here a glass beaker is held in a fluid with the same index, so zero light is reflected.

Waves (light in particular) travel at different speeds through different materials.  This speed is described by the “index of refraction“.  When a wave hits the interface between materials with different indexes of refraction it can reflect back.  The difference between the the indexes of stone and crystal and the index of air is pretty large and as a result a lot of light will reflect off of the air-to-stone boundary.  However, if there’s a layer of water the index steps up twice, from air to water, and again from water to stone.  It turns out that a more gradual stepping between indexes allows more light to make it from the air into stone without reflecting.

This additional color from a thin water layer isn’t a dramatic effect, especially compared to the “raised contrast effect” described above, but it’s not zero either.

Posted in -- By the Physicist, Physics | 9 Comments

Q: What would the universe be like with additional temporal dimensions?

Posted on June 4, 2012 by The Physicist

Physicist: This is a really nasty, complicated question.  It’s isn’t remotely straight-forward in the way that adding spacial dimensions is.  The universe we live in is “3+1 dimensional”, meaning 3 spacial dimensions and one temporal dimension.  While time and space do have more in common than you might think, they are still (no surprise) fundamentally different.

Because we live in a 3-D space, when we talk about what life is like in higher (spacial) dimensions we’re free to extrapolate from what we know life would be like in one dimension, how that changes when you move up to two dimensions, and how things are further generalized in three dimensions.  We can expect those patterns to continue into higher dimensions (example here!).  We’re even free to laugh haughtily at the pitiable denizens of a hypothetical one-dimensional world who are incapable of seeing how things behave in 2 or 3 dimensions.

Well, in terms of time that’s exactly the situation we’re in.  In the same way that a one-dimensional critter can know everything about where they are with a single number (like points along a ruler), a one time-dimensional critter (for example, everyone and everything) can know everything about when it is with a single number.  The fact that we use several numbers to designate time is an indulgence.

Having different numbers for the year, month, and day makes this solid gold calendar an indulgence. These numbers can be lumped together into just one number, because there’s only one time dimension.

Going from talking about points on a line (1-D) to talking about points in a plane (2-D) is a huge leap.  Suddenly have to concern yourself with trigonometry.  In a 3+2 dimensional universe, “temporal cartographer” could be a real job, and the working day would be “9 to 5 by 9 to 5”.

I wish I could offer up a reasonable guess about what life would be like with multiple time dimensions.  But just as a 1-D person can’t conceive of turning around, I can’t say what it means to “turn corners in time”.  Normally when presented with “what if” questions, you can ponder it in terms of how the laws of physics would change the least.  In this case they’re entirely up in the air.  For example, in physics it’s sometimes important to show that the past and future are different “places”.  This is so “obvious” that we take it for granted.  Regular rotations give us a way of “translating” any point into any other point that’s the same distance away.  That is; if you’re looking at something and you turn around, then that thing is behind you (physics is full of profound truisms like that).  Special relativity has provided us with another kind of “rotation” that exchanges some of one of the space directions with some of the time direction, but in a not-quite-as-simple way that involves a new kind of distance.

The set of points that are a fixed distance from the center in 2 D, in 1+1 D, and in 2+1 D.  Rotations can slide things around, but they don’t change distance.  Notice that a point in the future can slide around in the future, but it lives on a different “sheet” than a point in the past.

In regular space you can rotate, and in so doing, the relative position of everything around you traces out a circle.  In particular, things in front of you can end up behind you (Try it!  This post can wait.).  Rotation is just an interchanging of two space directions.  With special relativity comes the idea of the “Lorentz boost”, which is just a fancy way of saying “space-and-time rotation”.  When you go from sitting still to riding on a train, you’ve undertaken a Boost.  In the same way that physically turning around rearranges where things are (with respect to you), a Boost rearranges where and when events take place (with respect to you).  For example, when you’re not riding the train it shows up in lots of places at different times, but when you do ride it, it only shows up in one place at different times.  However, and this is the important part, the Lorentz Boost can’t take an event that’s in your future and rotate it into your past, or vice versa.

However!  With another time direction comes a new kind of rotation.  Ordinary rotation is an interchange of two space directions, Boosts are an interchange of a space direction and the time direction, and in 3+2 D space you can have a rotation that exchanges the two time directions.  Importantly, this new rotation can smoothly take events in your future and take them into your past.  That is to say; in 3+2 dimensional space you should be able to “turn around in time” and face the past.

I have no idea what that means.

It may be the case that some of our physical laws are symptoms of the dimension we live in.  For example, in a 1+1 D universe you’d have “conservation of directionality”, because nothing can turn around.  In our 3+1 D universe the fact that particles are only Fermions or Boson can be tracked back to the fact that we live in more than two (spacial) dimensions (very complicated details here).  However, there may be a lot of “laws” that are caused, at least in part, by the restrictions placed on us by the single time dimension we have to work with.

So, unfortunately, there are no actual answers to what the world would be like with more time dimensions, but (since it has nothing to do with reality) there’s no hurry to find those answers.

Answer gravy: Many of the most basic laws involve equations that are “ill-posed” in multiple time dimensions, and either don’t have solutions, or don’t make sense.  Almost every law in physics is written in terms of cause and effect, initial conditions to later conditions.  Extending that doesn’t sound terrible.  It seems like you could just extend the laws we have now, the same way you can for spacial dimensions, to work the same on each time direction the same way it does for just one.  But the laws we work with in physics just don’t extend in any useful way into higher dimensions without tacking on lots of weird extra restrictions that, in all but name, bring you back to a 3+1 dimensional universe.

The result of the initial conditions from one time direction will usually disagree with the initial conditions on the other times.  No matter how you define the initial conditions (what “initial” means in multiple time dimensions is an issue in itself), you’ll find that the initial conditions always cut across “characteristic lines”, which (this is not obvious) lead to a lack of solutions in general.  “Characteristic lines” are the paths that solutions to an equation “propagate along”, and having initial conditions on them basically means putting more information onto what should already be a solved problem.

For example, the sound that a speaker generates can be described easily using basic acoustic laws: the sound created by the speaker (initial condition) leads naturally to an easily calculable sound everywhere else (final conditions).  However, the sound created by a speaker traveling at the speed of sound, cannot be easily calculated, because the sounds the speaker makes all “stack up”; the speaker is continuing to make new sound on characteristic lines.  There are ways to deal with this, but they’re not “basic”, and required a lot more research.  The same mathematical complications crop up in effectively everything when multiple time dimensions are considered.

There’s a paper here that considers some workarounds in detail.

Posted in -- By the Physicist, Philosophical, Physics | 37 Comments

The 2012 Venus transit

Posted on May 30, 2012 by The Physicist

Physicist: There wasn’t a question behind this, but it’s worth announcing.

On June 5th or 6th (depending on where you are in the world) Venus will pass directly between the Sun and the Earth, so it’s basically a solar eclipse, but with Venus instead of the Moon.  In the last couple years there have been about a dozen Lunar eclipses and several solar eclipses.  However, Venus transits are very rare.  Unless you’re taking some seriously awesome vitamins, you probably won’t live to see the next transit in 2117.

The last Venus transit in 2004.

The transit will be happening for the better part of 7 hours.  It begins around 22:00 June 5th UTC and will continue until about 5:00 June 6th UTC.  For those of you in the Americas, that’s 3 pm Pacific / 6 pm Eastern on June 5th until after the Sun sets.  You can look up the exact time, city by city, here.

If you’re planning on looking at the transit take precautions.  There’s some very basic wiring deep in our brains that make us not want to look at the Sun.  Don’t fight it.  Even if you do try to see the transit unaided you’ll be too busy wiping your watering eyes and burning blind patches into your retinas to see anything.

Welding glasses are pretty cheap and let you look at the Sun (or welds) comfortably.  Also, while you may look like a jack-ass, wearing 4 or 5 pairs of shades at the same time does the trick as well.  Otherwise, you can use a magnifying lens to project a picture of the Sun onto a piece of paper.  Hold the lens in such a way that it projects a circle, then slowly move it back and forth until you see Venus.  More (useful) techniques here.

In addition to being a kick-ass thing that won’t happen again until the 64th Potus is in office (give or take), the Transit is a great chance for exoplanet hunters to practice their craft.  Exoplaneteers have been trying to read the composition of the atmospheres of planets around other stars when those planets transit by looking at the light that filters through their atmospheres.  By looking at the light filtering through Venus’ atmosphere they’ll be able to double-check their technique.  If the readings they get next week line up with what we already know the composition is (from probes that have physically been to Venus and sampled the air) then they’re on the right track.

Posted in -- By the Physicist, Astronomy, Experiments | 4 Comments