Q: Why haven’t we discovered Earth-like planets yet?

Posted on May 24, 2012 by The Physicist

Physicist: It’s amazing that we’ve found any at all, considering the difficulties involved.

The scale of things in space is ridiculous.  The closest discovered planet to us, outside of our solar system, is “Epsilon Eridani b“, a mere stone’s throw away at 10.4 light years.  If the Sun were about the size of a baseball, and for whatever reason was being kept in New York, then the star Epsilon Eridani would be about as far away as Paris (overland distance), the orbit of the planet Epsilon Eridani b would be a ring about 30 meters across, and the planet itself would probably be about the size of a pea.  “Probably” because while taking a picture of something substantially smaller than a bread box from 5,800 km (3,600 miles) away seems like it should be easy, astronomers still don’t have a way to do it, despite the extra time they have while all their friends are on dates.

Even contending with the fantastic distances, the fact that we’re looking for tiny dim things right next to gigantic bright things, and the fact that when you look at another solar system all you can see (even with the most powerful telescopes) is a single pixel of light, we’ve still managed to find over 760 planets around other stars (almost all in the last decade), up to as far as 27,700 light years away (a quarter of the way across the galaxy).

In our solar system we’ve found a mess of new planets (well, “dwarf planets” anyway) by taking pictures of the sky and literally looking for them.  However, to find extra-solar planets (“exoplanets”) we’ve had to rely on methods that are decent at finding planets that are huge and close to their suns, and bad at finding planets that are small and far from their suns.  That right there is the essential reason why we haven’t found any truly Earth-like planets yet: a planet like the Earth is too small and far from the Sun to be readily detectable.

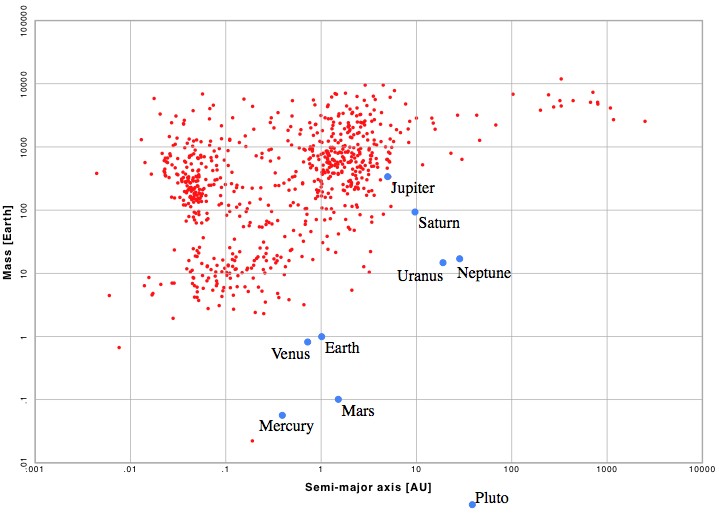
The orbital distances vs. to mass of the 767 exoplanets found as of May 2012. For comparison, the planets of our solar system are included. An alien civilization using techniques similar to ours might be able to see Jupiter, but not much more.

The most common techniques for finding exoplanets today are the “radial velocity” technique, and the “transit” technique.

An orbiting planet is whipped around in a huge circle by its host star, but at the same time the star itself is being moved in a tiny circle by its planets.  The effect is pretty small, but it does have some pretty interesting consequences.  In our solar system, there are two clusters of asteroids that share Jupiter’s orbit.  In a simple orbital system (with no “Sun wobble”) something the size of a planet quickly eats up everything that shares its orbit.  However, because Jupiter is heavy enough to literally make the Sun wobble, the situation is a bit more complicated, and the strange Jupiter-Sun-wobbliness dynamics lead to “Lagrange points“, where asteroids can orbits stably forever (it may be the case that all the planets have at least a few of these kinds of asteroids stuck in their orbits, but Jupiter’s are the easiest to find).  For astronomers however, the more important effect is that the physical movement of the star means that there is a slight (really slight) Doppler shift as the star moves forward and backward from the perspective of telescope on and around Earth.  When the star wobbles toward us it appears bluer, and when it wobbles away it appears redder.  For comparison, Jupiter causes the Sun to move back and forth at about 45 kph (28 mph).  45 kph is a hell of a lot slower than the speed of light, and as a result the reddening and bluing of the Sun by Jupiter is tiny.

In order to see this tiny Doppler effect it helps a lot to have a strong wobble, caused by a big planet orbiting quickly.  Star’s come in a wide range of different colors, so if it takes years for the star to wobble back and forth, it’s easy to assume that a star is a little extra blue or red because it’s hotter or colder instead of because of it’s movement.  But, if a star changes back and forth every few days, in a very regular cycle, then what you’ve probably found is a close-orbiting exoplanet.

The transit technique on the other hand is a little more forgiving.  The idea is that you stare at a star and wait for an eclipse.  When an exoplanet passes between us and its host star it causes the star to dim a little.  An alien civilization using this technique would see the Sun dim by about 0.0086% when the Earth was in front of it.  Unfortunately, the Sun and stars like it naturally change intensity by about 0.1% all the time, due to sunspots and other vagaries of “solar weather”, which completely drowns out the influence of Earth-sized planets.

Planet, sunspot, or smudge on the lens? Only time and statistical analysis will tell.

You can get around this using the fact that while the variation of a star’s intensity is mostly random, the variation due to a planet passing in front of it is extremely regular.  After watching for long enough you can detect the minute, repeated, dimming due to planets.  That said, what you’d really like is a big planet that can block out more light and make the dimming more pronounced, that also has a short orbit so that you can see it eclipse many times, which makes it a lot easier to tell the difference between natural variation and planet-caused variation.

Unfortunately, one of the draw-backs of the transit technique is that, at best, you’ll only spot less than 1% of the planets.  If it doesn’t eclipse, you’ll never see it.

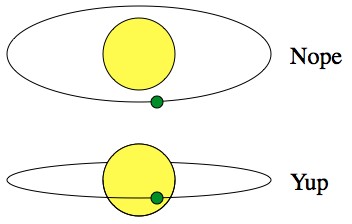
With respect to the Earth, the orbits of exoplanets are random. Sometimes they line up so that we can see them transit, but usually not.

Finding an Earth-like planet will require a lot of patience and more powerful telescopes and telescope arrays, but that’s just an engineering problem.  It’s just a matter of time (and probably not even that much!).  Once found, the next challenge will be to determine whether or not the newly found tiny-as-Earth planets are covered in plants and critters.  Already there are some ideas being floated that involve analyzing the atmosphere of the exoplanet to find signs of life (specifically, water vapor and oxygen).  As impossible as that sounds, considering that we can’t actually take pictures of exoplanets (and again, every time you look at a star you can’t do better than a point of light) we’ve actually managed to do it a few times!  Unfortunately, the first atmospheres we’ve seen were only visible because they were forming huge “comet tails” by being blown off of the surface of “hot-Jupiters” orbiting practically within high-fiving distance of their host stars.  So, not Earth-like, but it is a step in the right direction.

Chances are, we’ll find an Earth-sized planet inside of the goldilocks zone of another solar system, and be able to determine if there’s life on it or not, within the next few decades.  Copernicus would crap himself with joy if he were alive today.

Posted in -- By the Physicist, Astronomy | 4 Comments

Q: Is quantum randomness ever large enough to be noticed?

Posted on May 19, 2012 by The Physicist

The original question was: …true randomness on a quantum level has experimentally been shown to exist.  My question is, does this quantum randomness ever/often/always bubble up to our readily observable world of Newtonian physics to create truly random everyday events?

Physicist: Hard to say.

Quick aside: The difference between quantum randomness, which is absolute, and classical randomness, which basically means “very hard to predict”, is covered a bit in this older post.  In a nutshell, up until the science of quantum mechanics came along it was assumed that if you (somehow) knew everything about an object at one moment, you would be able to perfectly predict how it behaved the next.  However, it turns out that even if you know absolutely everything about a radioactive atom, for example, it’s still impossible to accurately predict when it will decay.  This is called “fundamental”, “irreducible”, or “quantum” randomness.  Back to the point:

Large scale effects can be thought of in terms of lots of small-scale effects being averaged together which usually (and counter-intuitively) leads to much more predictable (classical) results.  This is the same idea that shows up when you flip lots of coins: the total number of heads is very predictably about half.  Generally speaking, any individual quantum event will be drowned out by the noise of all of the other quantum events around it, and the average is the only important thing.

Large scale events that rely on a small number of atoms and interactions are likely to have the same kind of randomness as “legit” quantum phenomena.  For example, the meter on a Geiger counter is an example of quantum randomness on a large-scale.

A Geiger Counter detects radiation, including radiation from nuclear decay.

Nuclear decay is a quantum mechanically random process.  Normally, the effects of nuclear decay are washed out.  For example, you’re hit, on average, by about one high energy particle per exposed square centimeter every second.  Ever notice?  But a Geiger counter detects every high energy particle that passes through its detector (the wand on the right) and notes the event by moving a needle (which is huge by quantum standards) and clicking.  So, what Geiger counters and other sensitive detectors do is “exaggerate” tiny events and bring their effects into the macro-scale.

Normally, large-scale events are fairly well determined.  Whether or not you go to lunch is probably not particularly random.  If someone somehow got every possible piece of information about what everything in the nearby universe was doing, they’d be able to predict large-scale events, including your lunch schedule, with fair accuracy.

If you had complete knowledge about what the universe was doing, this would not be surprising. Unless of course, the dog were basing its decisions on quantum measurements of some kind.  But that would be weird.

However, if you determine whether or not to go to lunch based entirely on the results of a Geiger counter reading, then your lunch outing is a genuine, fundamentally random event.  This wouldn’t change the experience; you won’t see different versions of yourself walking around, and you won’t end up “spread thin” across different versions of the universe.  A quantum random number generator is essentially the same as an ordinary random number generator.

That all said, there’s chaos inherent to most of the stuff that happens in the world (tiny errors becoming bigger errors, becoming bigger errors, …).  However, there’s nothing particularly special about the original source of the errors being quantum mechanical.  As far as prediction goes, randomness due to quantum mechanics and randomness due to a lack of perfect knowledge (which is pretty hard to avoid) are pretty much the same.  This is a pretty subtle distinction.

You can expect that, after a lot of time, the randomness of quantum processes will lead to worlds that are wildly different from each other because of the butterfly effect.  But that’s pretty unsatisfying.  It would be more interesting to be able to point at a large thing in the world and say “that is dependent on just a couple of quantum events”.

The most dramatic example of exactly that is probably biological life.  The earliest development of a creature is strongly influenced by the interactions of a relatively small number of chemical interactions.  An atom in the wrong place in the flagella motor of a sperm can determine whether or not someone is born at all.  More than that, the evolution of entire species can be changed by a single mistake in the replication of a strand of DNA (this is one mechanism for mutation).

On a more individual basis, it’s hard to say how much the process of thinking is affected by the actions of just a few atoms.  The fact that you can lose a heck of a lot of brain cells without noticing implies that the activity of a handful of atoms probably isn’t too important when it comes to human behavior.  That said; maybe?

By the way, it’s a little dangerous to tread this close to the intersection between quantum mechanics and living things and consciousness in casual conversation.  To be clear, the important thing about life here is that it can change a lot based on the actions of just a few atoms.  Change a few atoms in a rock, and you’ve still got a nearly identical rock.  So the nature of the physical, gooey, grey matter is what’s important here, and not on the nature of consciousness itself.

In general, there probably aren’t too many day-to-day events that “turn on a quantum dime”.  The only exceptions (I can think of) is in the effects of the earliest, single-celled, development stage of complex organisms, when the actions of just a couple of atoms consistently result in very large changes later on, and in the lab, where sensitive equipment can detect and report on the fundamentally random actions of individual particles.

The highly predictable dog picture is from here.

Posted in -- By the Physicist, Biology, Physics, Quantum Theory | 11 Comments

Q: How is radiometric dating reliable? Why is it that one random thing is unpredictable, but many random things together are predictable?

Posted on May 12, 2012 by The Physicist

The original question was: Suppose there is a set of variables whose individual values are probably different, and may be anything larger than zero. Can their sum be predicted? If so, is the margin for error less than infinity?

This question is asked with the intention of understanding basically the decay constant of radiometric dating (although I know the above is not an entirely accurate representation). If there is a group of radioisotopes whose eventual decay is not predictable on the individual level, I do not understand how a decay constant is measurable. I do understand that radioisotope decay is modeled exponentially, and that a majority of this dating technique is centered in probability. The margin for error, as I see it presently, cannot be small.

Physicist: The predictability of large numbers of random events is called the “law of large numbers“.  It causes the margin of error to be essentially zero when the number of random things becomes very large.

If you had a bucket of coins and you threw them up in the air, it would be very strange if they all came down heads.  Most people would be weirded out if 75% heads of the coins came down heads.  This intuition has been taken by mathematicians and carried to its more difficult to understand, and convoluted, but logical extreme.  It turns out that the larger the number of random events, the more the system as a whole will be close to the average you’d expect.  If fact, for very large numbers of coins, atoms, whatever, you’ll find that the probability that the system deviates from the average by any particular amount becomes vanishingly small.

For example, if you roll one die, there’s an even chance that you’ll roll any number between 1 and 6.  The average is 3.5, but the number you get doesn’t really tend to be close to that.  If you roll two dice, however, already the probabilities are starting to bunch up around the average, 7.  This isn’t a mysterious force at work; there are just more ways to get a 7 ({1,6}, {2,5}, {3,4}, {4,3}, {5,2}, {6,1}) than there are to get, say, 3 ({1,2}, {2,1}).  The more dice that are rolled and added together, the more the sum will tend to cluster around the average.  The law of large numbers just makes this intuition a bit more mathematically explicit, and extends it to any kind of random thing that’s repeated many times (one might even be tempted to say a large number of times).

The exact same kind of math applies to radioactive decay.  While you certainly can’t predict when an individual atom will decay, you can talk about the half-life of an atom.  If you take a radioactive atom and wait for it to decay, the half-life is how long you’d have to wait for there to be a 50% chance that it will have decayed.  Very radioactive isotopes decay all the time, so their half-life is short (and luckily, that means there won’t be much of it around), and mildly radioactive isotopes have long half-lives.

Now, say the isotope “Awesomium-1” has a half-life of exactly one hour.  If you start with only 2 atoms, then after an hour there’s a 25% chance that both have decayed, a 25% chance that neither have decayed, and a 50% chance that one has decayed.  So with just a few atoms, there’s not much you can say with certainty.  If you leave for a while, lose track of time, and come back to find that neither atom has decayed, then you can’t say too much about how long it’s been.  Probably less than an hour, but there’s a good chance it’s been more.  However, if you have trillions of trillions of atoms, which is what you’d expect from a sample of Awesomium-1 large enough to see, the law of large numbers kicks in.  Just like the dice, you find that the system as a whole clusters around the average.

If there’s a 50% chance that after an hour each individual atom will have decayed, and if you’ve got a hell of a lot of them, then you can be pretty confident in saying that (by any reasonable measure) exactly half of them have decayed at the end of the hour.

In fact, by the time you’re dealing with a mere one trillion atoms (a sample of atoms too small to see on a regular microscope), the chance that as much as 51% or as little as 49% of the atoms have decayed after one half-life (instead of 50%) is effectively zero.  For the statistics nerds out there (holla!), the standard deviation in this example is 500,000.  So a deviation of 1% is 20,000 standard deviations, which translates to a chance of less than 1 in 1086858901.  If you were to see a 1% deviation in this situation, take a picture: you’d have just witnessed the least likely thing anyone has ever seen (ever), by a chasmous margin.

Using this exact technique (waiting until exactly half of the sample has decayed and then marking that time as the half-life), won’t work for something like Carbon-14, the isotope most famously used for dating things, since Carbon-14 has a half-life of about 5,700 years.  Luckily, math works.

The amount of radiation a sample puts out is proportional to the number of particles that haven’t decayed.  So, if a sample is 90% as radioactive as a pure sample, then 10% of it has already decayed.  These measurements follow the same rules; if there’s a 10% chance that a particular atom has decayed, and there are a large number of them, then almost exactly 10% will have decayed.

The law of large numbers works so well, that the main source of error in carbon dating comes not from the randomness of the decay of carbon-14, but from the rate at which it is produced.  The vast majority is created by bombarding atmospheric nitrogen with high-energy neutrons from the Sun, which in turn varies slightly in intensity over time.  More recently, the nuclear tests in the 50’s caused a brief spike in carbon-14 production.  However, by creating a “map” of carbon-14 production rates over time we can take these difficulties into account.  Still, the difficulties aren’t to be found in the randomness of decay which are ironed out very effectively by the law of large numbers.

This works in general, by the way.  It’s why, for example, large medical studies and surveys are more trusted than small ones.  The law of large numbers means that the larger your study, the less likely your results will deviate and give you some wacky answer.  Casinos also rely on the law of large numbers.  While the amount won or lost (mostly lost) by each person can vary wildly, the average amount of money that a large casino gains is very predictable.

Answer Gravy: This is a quick mathematical proof of the law of large numbers.  This gravy assumes you’ve seen summations before.

If you have a random thing you can talk about it as a “random variable”.  For example, you could say a 6-side die is represented by X.  Then the probability that X=4 (or any number from 1 to 6) is 1/6.  You’d write this as P(X=4) = \frac{1}{6}.

The average is usually written as μ.  I don’t know why.  For a die, \mu = 1\frac{1}{6}+2\frac{1}{6}+3\frac{1}{6}+4\frac{1}{6}+5\frac{1}{6}+6\frac{1}{6} = 3.5.  This can also be written, \mu=\sum_n nP(X=n), and often as E[X].  E[X] is also called the “expectation value”.

There’s a quantity called the “variance”, written “σ2” or “Var(X)”, that describes how spread out a random variable is.  It’s defined as \sigma^2= \sum_n (n-\mu)^2P(X=n).  So, for a die, \sigma^2= (1-3.5)\frac{1}{6}+(2-3.5)\frac{1}{6}+(3-3.5)\frac{1}{6}+(4-3.5)\frac{1}{6}+(5-3.5)\frac{1}{6}+(6-3.5)\frac{1}{6}=2.91666...

If you have two random variables and you add them together you get a new random variable (same as rolling two dice instead of one).  The new variance is the sum of the original two.  This property is a big part of why variances are used in the first place.  The average also adds, so if the average of one die is 3.5, the average of two together is 7.  So, if the random variables are X and Y with averages μX and μY, then μ=μX+μY.  And using expectation value notation (if you’re not familiar look here, or just trust):

\begin{array}{ll}Var(X+Y)\\= E[(X+Y-\mu)^2]\\= E[(X+Y-\mu_X-\mu_Y)^2]\\= E[((X-\mu_X)+(Y-\mu_Y))^2]\\= E[(X-\mu_X)^2]+2E[(X-\mu_X)(Y-\mu_Y)]+E[(Y-\mu_Y)^2]\\=Var(X)+2E[(X-\mu_X)]E[(Y-\mu_Y)]+Var(Y)\\=Var(X)+Var(Y)+2(E[X]-\mu_X))(E[Y]-\mu_Y)\\=Var(X)+Var(Y)+2(0)(0)\\=Var(X)+Var(Y)\end{array}

You can extend this, so if the variance of one die is Var(X), the variance of N dice is N times Var(X).

The square root of the variance, “σ”, is the standard deviation.  When you hear a statistic like “50 plus or minus 3 percent of people…” that “plus or minus” is σ.  The standard deviation is where the law of large numbers starts becoming apparent.  The variance of lots of random variables together adds, Var(X+\cdots+X) = N\cdot Var(X), but that means that \sigma_{x+\cdots+x} = \sqrt{Var(X+\cdots+X)} = \sqrt{N\cdot Var(X)}=\sqrt{N}\sigma_x.  So, while the range over which the sum of random variables can vary increase proportional to N, the standard deviation only increases by the square root of N.  For example, for 1 die the numbers can range from 1 to 6, and the standard deviation is about 1.7.  10 dice can range from 10 to 60 (10 times the range), and the standard deviation is about 5.4 (√10 times 1.7).

What does that matter?  Well, it so happens that a handsome devil named Chebyshev figured out that the probability of being more that kσ from the average, written “P(|X-μ|>kσ)”, is less than 1/k2.  Explanations of the steps are below.

\begin{array}{ll}i)&P(|X-\mu|>k\sigma)\\ ii)&=\sum_{|n-\mu|>k\sigma} P(n)\\iii)&\le\sum_{|n-\mu|>k\sigma} \frac{|n-\mu|^2}{k^2\sigma^2}P(n)\\iv)&=\frac{1}{k^2\sigma^2}\sum_{|n-\mu|>k\sigma} |n-\mu|^2P(n)\\v)&\le\frac{1}{k^2\sigma^2}\sum_n |n-\mu|^2P(n)\\vi)&\le\frac{1}{k^2\sigma^2}\sigma^2\\vii)&=\frac{1}{k^2}\end{array}

i) “The probability that the variable will be more than k standard deviations from the average”.  ii) This is just re-writing.  For example, if you have a die, then P(X>3) = P(4)+P(5)+P(6).  This is a sum over all the X that fit the condition.  iii) Since the only values of n that show up in the sum are those where |n-μ|>kσ, we can say that 1<\frac{|n-\mu|}{k\sigma} and squaring both sides, that 1<\frac{|n-\mu|^2}{k^2\sigma^2}.  Multiply each term in the sum by something bigger than one, and the sum as a whole certainly gets bigger.  iv) “1/k2σ2” is a constant, and can be pulled out of the sum.  v) If you’re taking a sum and you add more terms, the sum gets bigger.  So removing the restriction and summing over all n increases the sum.  vi) by definition of variance.  vii) Voilà.

So, as you add more coins, dice, atoms, random variables in general, the fraction of the total range that’s within of kσ of the average gets smaller and smaller like \frac{1}{\sqrt{N}}.  If the range is R and the standard deviation is σ, then the fraction within kσ is \frac{k\sqrt{N}\sigma}{NR} = \frac{1}{\sqrt{N}}\frac{k\sigma}{R}.  At the same time, the probability of being outside of that range is less than 1/k2.

So, in general, the probability that you’ll find the sum of lots of random things away from their average gets very small the more random things you have.

Posted in -- By the Physicist, Combinatorics, Math, Particle Physics, Probability | 9 Comments

Q: Is the final step in evolution an ascension into an energy-based lifeform?

Posted on May 6, 2012 by The Physicist

Physicist: Awesome question!  The very short answer is: nope.

Energy beings are an old staple of sci-fi (a good one), but they’re almost certainly impossible, or at least, it’s almost certainly impossible for life (as we know it) to evolve into energy.  Even after billions of years on Earth, life is pretty much the exact same stuff that it’s always been.  Several billion years ago single cells figured out how to metabolize, repair damage, and reproduce.  Everything since then has pretty much just been variations on that theme (sincerest apologies to our evolutionary biologist readers).  The word “evolution” evokes ideas of advancement, and improvement, and ascension, but “in practice” evolution is to accidents as a beach is to grains of sand.

Energy Beings: The ultimate end of evolution, or possibly a dude in a body sock.

Part of that is that there’s no goal that life is evolving toward, or even a path that life is taking.  So, humanity is no more the pinnacle of evolution than every other living thing is.

One of the classic examples of evolution in action is the Peppered Moth.  The Peppered Moth, like many species (including people!), appears in a couple different colors and patterns.  Normally they’re grey (and peppered), but during the industrial revolution the area around London became so nasty and coal-covered that black peppered moths became far more common.  By accident of birth, some moths were black and, by accident of circumstance, they found that they could hide from predators better than their suddenly very visible grey cousins.  That’s evolution; it’s not a matter of being better, or even adapting, it’s just a matter of stumbling forward and whatever happens happens.

It would be great if evolution always made things more advanced, but in general, creatures only become as complex as they minimally need to be.  If group of critters can get along by becoming simpler, then tend to evolve (accidentally be born) into that simpler form.  For example, there are several examples of blind subterranean animals that are descended from species that once had eyes.  Again, it’s not that they purposely evolved to be blind, it’s just that sometimes (by accident) you’re born without eyes, and sometimes it doesn’t matter (because you live in a cave).  It’s a lot easier (more likely) to lose a feature and become simpler than it is to gain a new feature and become more complex.

Nothing to see here.

It is the case that the lifeforms with the greatest complexity will be found later in history rather than earlier, but that’s pretty much because it takes time for things to become complex.  However, for the most part living systems have maintained about the same level of complexity for hundreds of millions of years.  The most successful form of life on Earth (arguably) is still single-celled.  Those little dudes really have it all figured out.

Long story short: evolution isn’t “leading up” to anything, it just drunkenly limps along using the same set of tricks in slightly different orders.

On the physics side of things, “energy life” sounds like a cool idea, it’s not really a possibility (as far as we can say).  Energy generally doesn’t exist on its own without matter, and when it does it’s propagating about at the speed of light (for example: light).  Not experiencing time (which is one of the problems with light speed) seems to go against the idea of “life”.  That is, if something never changes at all, can it really be alive?

The concept we (sci-fi aficionados) usually have of energy beings, as a kind of beneficent glowing ghost or a giant Kirk-harassing cloud, runs contrary to the physical understanding of energy physicists have developed so far.  Despite all the different terms that are used to talk about energy, it only takes a couple forms.  At its most base there’s the “energy of stuff” (like the E=mc2 of matter), there’s the “energy of stuff moving” (kinetic energy), and there’s the “potential for stuff to move” (the various forms of potential energy: charged batteries, gasoline, wound clock springs, etc.).  A “ball of energy” that’s independent of matter isn’t really a thing.

It would be cool to think that someday something will “evolve into energy”, but pressed for a prediction, I’d say that evolution will continue to stumble around at random for as long as there are living things around to do the stumbling.  Evolution is a process of accidental baby steps, and turning into an energy being, even assuming it’s possible, is more of a leap.

Posted in -- By the Physicist, Biology, Evolution, Physics | 23 Comments

Q: What would life be like in higher dimensions?

Posted on May 1, 2012 by The Physicist

The original question was: Assuming we had four (or more) spatial dimensions in which to freely move around, like say a 4+1 dimensional universe, how might one extend our 3+1 dimensional physics to that universe?

Side note: When someone says “3+1 dimensions”, what they mean is “3 regular space dimensions, and one time dimension” which is exactly the situation we live in (apologies to our pan-dimensional readers).

Physicist: Right off the bat, more dimensions means more freedom of movement.  One of the more mundane effects of that is that in 4 dimensional space there’s an extra direction you can move and/or fall over in.  So if you want to build a working bar stool you’d need at least 4 legs instead of just 3.  In fact, in D-dimensional space bar stools need at least D legs, or they’ll fall over.  Just one of the subtle economic effects of higher dimensional living.

You’d also find that in 4 or more dimensions, you’d be able to do a lot of tricks impossible in 3 dimensions, like creating Klein bottles or (equivalently) taping the edges of two Möbius strips together.  Sailing knots could take on stunning complexities.  In fact, they’d need too!  All of the knots that work in 3 dimensions fall apart immediately in 4.

In four dimensions you could make this surface without worrying about it intersecting itself.

Most physical laws are already written in a dimension-free form.  For example, in Newton’s second law, \vec{F}=M\vec{A}, \vec{F} and \vec{A} are both vectors, but they can be vectors in any number of dimensions.  So you can use \vec{F}=M\vec{A} for objects on a line (1-D), on a table-top (2-D), in space (3-D), or whatever (whatever-D).

There are some laws that are usually written in a 3-D form, but that’s generally a matter of convenience more than necessity.  For example, we talk about the “angular momentum vector”, which is defined to be perpendicular to the plane of rotation.  It’s convenient because in three dimensions there’s always exactly one perpendicular direction to a plane, whereas in 4 dimensions (for example) there are 2.

In 3-D we can formulate laws about spinning things in terms of the one direction that isn’t spinning (h), the “axis of rotation”. But we can always formulate laws in terms of the two directions that are spinning, regardless of dimension.

This is pretty easy to fix and generalize, it just becomes a little more difficult to work with.  All that said, while our physical laws can be generalized to any number of dimensions, the manifestation of those laws are wildly different.  So, living in higher dimensions would be pretty alien.

Based on our understanding of gravity (gained from studying this podunk universe), gravitational force should drop by \frac{1}{R^{D-1}}, where D is the dimension and R is the distance between the objects in question.  It so happens that because of the nature of orbits, a stable orbit can only exist in 2 or 3 dimensions.

The “effective potential” representing the balance between the gravity and centrifugal forces of an orbiting object.  Orbits can be stable in 2 and 3 dimensions. In all other dimensions planets and moons will always either spiral in or fly away.  Shown here is the potential energy from gravity and the centrifugal force combined.  If there’s a “cup” you can form a “bound orbit” in it.

In 4 or more dimensions orbits are always unstable, and in 1 dimension the idea of an orbit doesn’t even make sense.

Most physicists consider light to be native to only 3 dimensions, because light is an EM wave and it’s direction of propagation is perpendicular to both its Electric and Magnetic fields.  (Fun fact: the direction that light points is called the “Poynting vector“, after John Henry Poynting.  Life’s funny.)  In 4 or more dimensions this direction isn’t unique, and in two dimensions there’s no direction at all.  However, you can express EM waves just in terms of “E” in any dimension without problem.

Assuming light can exist in higher dimensions, it would behave very strangely.  Sound waves too.  In odd dimensions other than 1 (3, 5, 7, …) waves behave the way we normally see and hear things: a wave is formed, it moves out, and it keeps going.  However, in even dimensions, and 1 as well, (1, 2, 4, 6, …) waves “double back” on themselves.  You can see this in ripples on the surface of water (2-D waves).  Ripples are more complex than just a ring; the entire circle within the ripples is disturbed.

In even dimensions (like the 2-D surface of water), waves propagate in a more complex way than we’re used to.  Instead of a simple pulse, you get an “area filling” wave.

If you set off a firecracker in 3, 5, 7, etc. dimensions, then you’ll see and hear the explosion for a moment, and that’s it.  If you set of a firecracker in 4, 6, 8, etc. dimensions, then you’ll see and hear the explosion intensely for a moment, but will continue to see and hear it for a while.  For light the effect would be fairly subtle, except for extremely long-distance effects, like somebody reflecting a bright light off of the moon.  You probably wouldn’t notice the effect day-to-day.  However, it would ruin the experience of sound.  In 4 dimensional space the firecracker, even in open air, would sound like thunder; loud at first, and leading into a drawn out boom.  It may not even be possible to understand people when they speak.

All the fundamental particles should still exist, but how they interact would be pretty different.  Which elements are stable, and the nature of chemical bonds between them, would be completely rearranged.  Some things would stay the same, like electrons would still have two spins (up or down).  But atomic orbitals, which are determined by spherical harmonics (which in turn are more complicated in higher dimensions), would generally be able to hold more electrons.  As just one example (for our chemistry-nerd readers), you’ll always have 1 S orbital in every energy level, but in 4 dimensions you’ll have 4 P orbitals in each energy level, instead of the paltry 3 that we’re used to.  This messes up a lot of things.  For example, in 4 dimensions Magnesium would be a noble gas instead of a metal.  Every element after helium would adopt weird new properties, and the periodic table would be longer left-right and shorter up-down.

So, while the laws of physics are actually the same, if you lived on a four-dimensional Earth in a four-dimensional universe you’d find that (among other things): your bar stool may need an extra leg, Earth wouldn’t be able to orbit anything, you’d never be able to hear anything crisply, and the periodic table of the elements would be seriously rearranged.

Posted in -- By the Physicist, Physics | 72 Comments

Q: How much does fire weigh?

Posted on April 26, 2012 by The Physicist

The original question was: So I was wondering, and I have pondered it for some time, since fire is a plasma, and plasma is a state of matter. and matter is defined as anything that has mass, would that then mean that fire has mass and weight to it? If so, is there a way to measure its weight? How much space would, say, a pound of fire take up?

Physicist: It weighs more than nothing, but if you’re at the bottom of a pillar of fire, being crushed should be your second concern.

Fire: bad.

Fires, putting aside details about plasma and chemicals or whatever, is just hot air.  For a given pressure the ideal gas law says that the density of a gas is inversely proportional to temperature, in Kelvin.  You can use this fact, the temperature and density of air (300°K 1.3 kg/m3), and the temperature of your average run-of-the-mill open flame (about 1300°K) to find the density of fire.

For most “everyday” fires, the density of the gas in the flame will be about 1/4 the density of air.  So, since air (at sea level) weighs about 1.3 kg per cubic meter (1.3 grams per liter), fire weighs about 0.3 kg per cubic meter.

One pound of ordinary fire, here on Earth near sea level, would take up a cube about 1.2 meters to a side.  The reason that fires always flow upward is that its density is lower than air.  So, fire rises in air for the same reason that bubbles rise in water: it’s buoyant.  Enterprising individuals sometimes even take advantage of that fact.

Fire: good.

If you were on a planet with no air at all, fire would fall to the ground instead of rise because, like all matter, it’s pulled by gravity.  Also, it would be hard to keep the fire going (what with there being no air).

Posted in -- By the Physicist, Physics | 19 Comments