Q: Half-life?

Posted on August 20, 2019 by The Physicist

The original question was: If you have a lump of radioactive material with a half life of say 10,000 years, then how come it could start steadily decaying right away? Why wouldn’t everything be relatively stable for 10,000 years and then all of a sudden half of it decays? Like if you buy eggs from the store with an expired date in 2 weeks, you wouldn’t expect one egg to go bad 2 days later, and then another 2 days after that and so on. You’d expect them all to start going bad around the same time.

Physicist: Eggs have an age that they’re “aware” of, in the sense that they change in a predictable way.  For example, a fresh egg doesn’t (yet) have a bird in it, while an old egg is either empty of fowl or is foul.  By looking at or smelling an egg you can get a sense of how old it is.  That’s not true of atoms.

If you know the number of protons, neutrons, and electrons in an atom, then you’re done.  There is literally nothing more to know.  An atom of carbon-12 (regular carbon) that’s billions of years old is, in every physical sense, totally indistinguishable from a carbon-12 atom created moments ago.  In other words: atoms are ageless.

Like the (original) Highlander, atoms don’t age.  Unlike the Highlander, there can be several.

Elements are distinguished by the number of protons, which is the same as the number of electrons, which determines all of the important chemical properties.  Different isotopes of an element are distinguished by the number of neutrons.  Some isotopes are radioactive and just kinda fall apart, producing alpha, beta, gamma, or neutron radiation (depending on the isotope).  Rutherford named the first three in ascending order of penetrating power.  A couple pieces of paper will stop most alpha and beta radiation so, since you have skin, gamma rays are the only kind really worth worrying about.

When an atom will decay is unpredictable and doesn’t change with time.  A given radioactive atom has some probability of decaying in the next five minutes, say between 12:00-12:05.  If it’s still around at 12:05, then it has exactly the same probability between 12:05-12:10.  In fact, since no particular time is special, the probability is the same between 12:03-12:08 or any other five minute block.

The more time an atom sits around, the more likely it is to decay.  It’s continuously “rolling the dice” to decay or not, and the longer it exists the more opportunities it has.  So there will never come a time when the probability of decay is 100%, but given enough time, a radioactive atom is eventually more likely than not to decay.  That means we can’t talk about the lifetime of an atom, the time it will take to definitely decay, but we can talk about the “half-life”, the time it will take for the chance of decay to be 50%.

If every minute 20% of the atoms in a sample decay, then at the end of every minute you’ll have 80% of the atoms you had at the beginning of that minute.  Here each column is 80% the height of the column to its left.  There’s a time where you’ll have lost 30%, or 50% (the half-life), or even 99%, but you’ll never quite lose 100%.

For example, if the probability of decay is 20% in a minute, then at the end of one minute there’s an 80% chance the atom will still be around.  After two minutes that chance is 64%, which is 80% of 80%.  After three minutes the chance is 0.512 = (0.8)3, or 51.2%.  This is because in order for the atom to survive three minutes it has to survive the first and the second and the third, and the chance each time is 80%, because nothing changes (if it doesn’t decay).  Following this rule you never get to zero, but you do get to half after a little more than three minutes.  This exponential drop is due to the fact that nothing changes for the ageless atoms over time: as far as nuclear decay is concerned, every minute is the same as the one before.

If the half-life of an isotope is h, then the probability, p, that a particular atom will still be around after some amount of time, t, is p=\left(\frac{1}{2}\right)^{\frac{t}{h}}.  What this is saying (in mathspeak) is that after every half-life, the probability that an atom will remain is halved.  For example, at t=2h (after two half-lives), p=\left(\frac{1}{2}\right)^{\frac{2h}{h}}=\left(\frac{1}{2}\right)^2=\frac{1}{4}.

There’s nothing special about any particular amount of time.  You can plug any amount of time you like into that equation.  For example, if h=5 minutes, then after t=7 minutes, the probability that an atom won’t have decayed is p=\left(\frac{1}{2}\right)^{\frac{7}{5}}\approx0.379=37.9\%.

There’s isn’t even anything special about half-lives.  If you get a urge to go rogue on the scientific establishment and start using fifth-lives (and who doesn’t?), you can!  If the fifth-life (the time at which an atom has a 1 in 5 chance of not yet decaying) is f, then the probability that it’s un-decayed after time t is p=\left(\frac{1}{5}\right)^{\frac{t}{f}}.

Normally when you hear about half-lives, it’s in the context of how much of a sample decays in a certain amount of time and not about the lifetimes of individual atoms.  Fortunately, “the fraction of a sample that decays” and “the probability of an atom decaying” are one and the same.  In practice, you measure probabilities with a large number of trials and fall back on the aptly named law of large numbers to nail down your results.  For example, if you wanted to show that the probability of getting tails when you flip a coin is 50%, you’d flip a bunch of coins, divide the number of tails by the total number of flips, and the larger the number of coins the closer the result will be to 0.5 (if you have an afternoon and literally nothing else to do, try it).

As luck would have it, by the time your sample is large enough to see, you’ve got an inconceivable number of atoms.  When the amount of radiation exuding from a sample drops by half, there must be half as many radioactive atoms radioacting, and (since there are a large number of them) the probability that any particular atom has decayed must be 50%.  But if you’ve only got a few atoms to work with, there’s really no telling (beyond rough estimation) what fraction will be around at any given time.

Typical half-lives are on the order of thousands to billions of years.  I say “typically”, because isotopes with really short half-lives are viciously radioactive and decay into other elements quickly, while isotopes with long half-lives can last long enough for some podunk human to find them.  For example, uranium 238 (which makes up more than 99% of natural uranium) has a half-life of about 4.5 billion years.  That means that it’s barely radioactive and a fair fraction of it will last from whatever stellar cataclysm created it before the formation of our solar system (about 5 billion years ago) to today.  And the uranium that remains doesn’t show its age: it’s just as useful, dangerous, and potent as when it was a precocious tyke, drifting around in deep space.

Posted in -- By the Physicist, Logic, Particle Physics, Physics, Probability | 8 Comments

Q: What’s the point of going to the Moon?

Posted on July 19, 2019 by The Physicist

Physicist: We imagine interplanetary spacecraft as massive, expensive rockets, but the Moon changes that.  Spacecraft built and launched from the Moon don’t have to have huge boosters; even tiny spacecraft can travel across the solar system efficiently.  We should go to the Moon because, if and when humanity expands into space, the Moon will be a major hub of transportation and industry for our Home World.  It turns out that the biggest difficulty with spaceflight isn’t space, it’s Earth.  And the Moon is notably not Earth.

That said, the pictures you’ve seen of the surface of the Moon are about right.  It’s a terrible place.  The Moon is the Ft. Lauderdale Airport of space; you only go there so you can go somewhere else.

The Moon is a whole lot of this, so don’t forget where you parked.

Our Moon (the Moon) is ludicrously big relative to the Earth.  The other moons in the solar system are tiny compared to their host planet and likely formed in place or were captured.  The leading theory for the formation of our Moon is the “giant impact hypothesis”: another planet hit the Earth (more accurately two planets hit each other, neither/both of which were the Earth) around 4.5 billion years ago and “splashed” a huge amount of material into orbit which coalesced into the Moon.  We suspect that this is the case, in part, because the samples brought back show that the surface is made of roughly the same stuff as the Earth and was once entirely molten.  That’s about what you’d expect from slamming a couple planets together: space lava.  The lightest of that lava was the first to solidify into a surface, leaving anorthosite for us to find.  So for the most part, the stuff we expect to find (and have found) on the Moon can also be found here.  The big difference isn’t material, it’s history.

The lowlands are the dark regions, which are younger (a mere 3.2-4.2 billion years old) and formed by volcanoes.  The highlands are older and formed when the Moon first cooled.  And Earth is where you live (for now!).

Without a magnetic field to deflect solar wind and cosmic rays, or an atmosphere to burn up meteors, the surface of the Moon has spent the last several billion years getting pulped and nuked.  Other than outcrops of bedrock poking through the surface, the entire Moon is covered in a layer of fine regolith several meters deep.  This layer is the result of being melted and smashed by rocks from pebbles to mountains traveling around mach 60 (~20 km/s plus or minus a lot), all the while being irradiated by direct exposure to space and the Sun.  Lunar regolith is basically an endless sea of dust and ground glass.  It’s so fine that it both floats and sticks to everything electrostatically, so sharp that it damages everything it touches, and so omnipresent that there’s no escape from it.  There are some clever uses for it, like using 3D printers to turn it into Moon-mud houses, but most of the time it’s just across-the-board-awful.

Eugene Cernan (Apollo 17) reported that “… one of the most aggravating, restricting facets of lunar surface exploration is the dust and its adherence to everything no matter what kind of material, whether it be skin, suit material, metal, no matter what it be and it’s restrictive friction-like action to everything it gets on” and Alan Bean (Apollo 12) kvetched that “… dust tends to rub deeper into the garment than to brush off”.

If you went to live on the Moon, the dust is the first thing you’d notice.  That said, the dust and radiation are manageable.  For the dust you just need a hygiene protocol to keep dust and people as separate as possible.  This wasn’t really an option for the Apollo missions, which had to work from one small room with no airlock.  When the world outside your front door is a nightmare, sleeping in the mud room is not ideal.

To deal with a surface that’s continually pelted with radiation and space bullets, the solution is simple: don’t be on the surface.  With a dozen meters of rock between you and the sky, a lot of things get easier.  No radiation, no meteors, and no extreme temperature swings (-173°C to 127°C).  Luckily, we won’t even have to dig.  There are hundreds of holes opening into massive ex-lava tubes running under the lunar surface.  These tubes are protected from the sky, while maintaining the average lunar temperature of -21°C.  Earth would have the same temperature (since we’re the same distance from the Sun), except that we’ve got an atmospheric greenhouse effect working for us (as if you needed yet another reason to be pro-air).

A “skylight” in the roof of a lava tube under Mare Tranquillitatis.  Some of these tubes have been determined to be several hundred meters across. We can literally build cities in these things (with very simple subway systems).

That -21°C is a lot warmer than it sounds.  Without air it’s difficult to get rid of heat, so cold isn’t really a practical issue in space.  To experience the difference between the efficiencies of radiating heat vs. conducting/convecting heat, first sit next to a fire, then sit above it.

So the Moon is (unlikely) to be harboring mountains of gold.  It’s Earth-stuff piled up in a remarkably unpleasant environment.  But the Moon does have a few big selling point: it exists, it’s high up yet close by, and it’s not Earth.

Launching material from the surface of the Earth is really, really hard.  Between Earth’s gravity and air, we live in one of the worst positions in the solar system for spaceflight.  There’s a nigh-impenetrable wall between Earth and low orbit, an 8 km/s speed requirement, which is why launch vehicles look more like skyscrapers than spaceships.  But once you’re up there, moving from place to place in space is comparatively easy.

Being small means that it takes relatively little energy to escape the Moon’s gravity and being so far from Earth means that Earth’s gravity can practically be ignored.  To escape from Earth’s gravity from the surface your rocket needs to “pay a cost”: acceleration up to 11.2 km/s.  To escape from as high as the Moon’s orbit, you only need to pay about 0.5 km/s toward fighting Earth’s gravity.

The Moon sits almost all the way out of the Earth’s gravitational potential well (left).  The Saturn V (middle) was needed to launch the Command Module and LEM to lunar orbit, but the tiny Command Module (right) was all that was needed to come back.  To get a sense of scale, the Saturn V rocket is about the size of Statue of Liberty and the Command Module is about the size of a truck (like those in the background of the Saturn V image).

It’s hard to emphasize how much of a head start launching from the Moon gives us.  Had they been so inclined, the Apollo astronauts could have gone awol and flown the Command Module to Mars instead of returning home.  Their humble spacecraft was capable of accelerating as much as 2.8 km/s and to get to Mars from lunar orbit only requires about 2.2 km/s.  They would have run out of air long before they arrived and they wouldn’t have had the fuel to slow down, but the point is that they had the option to be the handsomest corpses to ever impact the Martian surface (an honor they bravely passed up).

So to build actual spacecraft and cities we have to do it off-world.  There just isn’t another option.  Building colossal rockets to put itty-bitty payloads into space is silly, so it’s our good fortune that the Moon exists.  There’s all the makings of spaceships, habitats, fuel, and even food up there; it’s just a matter of processing it.

Earth’s 23.5° tilt means that every point on Earth will be exposed to the Sun at some point during the year.  But the Moon has a far more modest 1.5° tilt, which means that the bottom of craters near the poles never see the Sun.  These Craters of Eternal Darkness (that is seriously the name) are among the coldest places in the solar system, -247°C, a balmy 26°C above absolute zero.  Without sunlight, these craters are able to sustain water ice that isn’t found elsewhere.  It’s estimated that there is on the order of a billion tons of water, about a cubic km, of ice buried in those polar craters, which is great news.  Water means easily accessible hydrogen for fuel, oxygen for breathing, water for drinking, and ice cubes for space whiskey.  There are already plans in the works to start exploiting this resource, so that the Moon can be a fuel depot for trips farther out into the solar system.

Fortunately, the Craters of Eternal Darkness are rimmed by Peaks of Eternal Light (I am not making this up), which always see the Sun on the horizon.  That means that unlike everywhere else on the Moon, a base at the poles never has to go without sunlight (and solar power), unlike the rest of the Moon which has two weeks of light and two weeks of night every lunar month.

Maps of the water ice detected around the south (left) and north (right) poles of the Moon.  These maps cover 10° of latitude, which is an area about the size of Italy.

This ice seems to be fantastically old and was likely deposited by comets.  Not to get too far ahead of ourselves, but that means that lunar ice is a non-renewable resource.  A billion tons sounds like a lot, until you consider that we’ve dug up and burned over 20 billion tons of oil in the last century and a half here on Earth.  I’m sure it won’t be an issue.

But just in case it is, there are more elegant ways to get to and from the lunar surface: by rail.  One of the big advantages of not having an atmosphere is not having a speed limit.  To get from the surface of the Moon to the top of Earth’s atmosphere requires about 5.9 km/s.  In Earth’s atmosphere 5.9 km/s is thoroughly fatal, but on the Moon the only way to notice that kind of speed is to look out a window.

Mass Drivers: An elegant mode of space travel.

A “mass driver” is basically a maglev train.  Magnets support and propel the spacecraft along a rail until it reaches the desired speed.  For an acceleration of 3 g’s (what you experience in a Gravitron ride at the fair) you’d need a rail 592 km long and passengers would only have to be uncomfortable for a little over three minutes.  For cargo that definitely doesn’t need to survive the journey, you can ramp up the acceleration and shorten the rail by the same factor.

So why go to the Moon?  It’s the first, most important step in expanding into the universe and eventually eliminating humanity’s industrial impact on Earth.  The Moon is a platform that we can use to bring ourselves and our ambitions into the heavens.

Also science.  But of course, it’s much easier to learn about a place when you live there.

Posted in -- By the Physicist, Astronomy, Engineering, Physics | 14 Comments

Q: How hard is it to build a space elevator? What’s the point?

Posted on June 19, 2019 by The Physicist

Physicist: Right around the end of the 19th century, Konstantin Tsiolkovsky (of rocket equation fame) got to thinking about how a taller version of the Eiffel tower, built on the equator, might be a good way to get things into orbit.  It turns out that the craziest part of that idea isn’t the space part, it’s the tower part.  If you want to build an elevator to space, you don’t put it in a tower, you hang it from the sky.  Obviously.

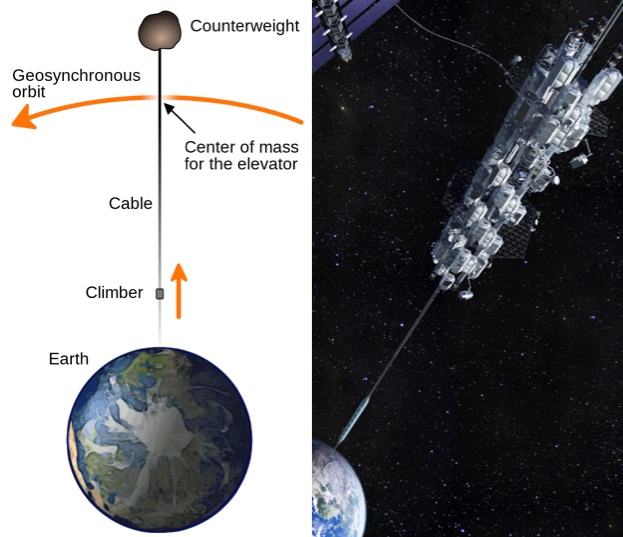
The basic set up for a space elevator.  Above geosynchronous orbit, 42,000 km up, the tether will swing fast enough that it will “fall up”, keeping the whole system upright.

In order to build a space elevator we’d first send a bundle of cable to geosync (or manufacture it in space) and then lower one end to the ground.  Once it’s anchored, we’d get new cables into place by running them up the old cables like a flag pole.

The cost of sending stuff to space has dropped precipitously in the last few years, as people of staggering genius discovered not-throwing-your-rocket-away technology.  But even with reusable equipment, rocket flight has a number of drawbacks that are unlikely to ever be fixed.  Rockets are powered by rocket fuel, which means that there’s a whole extra process for supplying them energy.  And since a rocket needs to carry all the fuel it burns, the first (and largest) stage of a rocket is almost entirely fuel used to lift other fuel.  And then of course are all of the usual issues that crop up when you ride an explosion into space.  It’s good that the lower stages are now being reused, but it’s bad that they exist at all.

“The usual issues”

Vehicles that climb up and down a space elevator can be as small as you like, run on electricity, and don’t suffer from the burning/exploding snafus native to rocketry.  While the trip will be much slower and controlled, more like travel by train than roller coaster, the real advantage of space elevators is infinite free energy forever and a safe, convenient way to get to and from the surface of Earth and literally anywhere else in the solar system.  Since the tether is anchored to the ground, the rotation of the Earth supplies sideways velocity to anything attached to the tether and (like anything that rotates) that sideways velocity adds up to a lot if you get far enough out.

The higher something is, the longer it takes to orbit.  Near the surface (within a few hundred km) orbits around the Earth take about 90 minutes, while the Moon (385,000 km away) takes about a month.  One Lunar month in fact.  In between is “geosynchronous orbit”, where objects can orbit the Earth in exactly one day, allowing them to stay over a single point on the equator indefinitely.  If you ever see a satellite dish that’s nailed to a wall, it’s pointing at a satellite in geosync, because only those satellites sit perfectly still in the sky with respect to the ground.  If you run a cable from the equator straight up, below geosync it will want to fall, because it will be traveling slower than orbital speed (that’s why ropes don’t stand up on their own), but above geosync it will want to fall up, because it will be traveling faster than orbital speed.  If you swing a rope around over your head it will point straight away from you and for exactly the same reason space elevators stay upright (as long as enough of its mass is above geosync).  Basically, space elevators turn Earth into a giant space weed wacker.

The big hurdles to building a space elevator are: 1) it sounds like a physicist stoner fantasy and 2) for Earth there are only a few things you can build a space elevator out of and we can’t manufacture any of them on the scales we need.  The first problem is an old one: electricity, radios, computers, satellites, and practically every other important advancement were deemed impossible and pointless right up until they became easy and essential.  The second problem is a bit more fundamental.

A hanging rope has to hold up its own weight in addition to whatever is tied to it.  There’s a limit to how far a rope can hang before it snaps under its own weight, called the “breaking length”.  Perfect name.  The breaking length is a function of both the density of the material and the tensile strength; it’s greatest for materials that are light and strong.  Unfortunately, the breaking lengths for our usual building materials is a little short.  For example, the breaking length for steel is about 6.4 km.

These musical pipes haven’t snapped under their own weight because they’re shorter than 2.5 km, the breaking length of copper.

So why no just make the top of the cable thicker than the bottom?  On the scale of sky scrapers that’s exactly what we do.  But on the scale of the sky itself, it’s silly.  Since the cable is pulled in both directions away from geosync, it needs to be thickest there; geosync is “the top of the hill”.  By declaring that you’d like the tension to be constant along the entire cable (the best way to avoid snapping), you can derive how many times thicker it needs to be at geosync compared to its size at ground level (or wherever else you’d prefer).  This is the “taper ratio”.  Building a space elevator out of steel would entail a taper ratio of around 10175, meaning that a steel cable that’s 1 cm on the ground would have a diameter of around 1060 times the size of the observable universe at geosync, which would be difficult to construct for… any number of reasons.  Carbon nanotubes on the other hand have a breaking length of around 6,000 km and a taper ratio of 1.6 between the ground and geosync.  Even if you make the ratio 100, to accommodate extra equipment, lots of climbers, and a generous safety margin, that’s still totally feasible.  It might look a little weird if you looked at the geosync station and the ground anchor at the same time, but you can’t: they’re 36,000 km apart.

The problem is that carbon nanotubes don’t come in 40,000+ km lengths.  The record so far is about half a meter.  That’s really impressive for a single molecule, but it would be nice to have intact strands stretching the full length of the tether, rather than tying or gluing them together (which introduces weak points).  That right there is the big stumbling block for actually building space elevators: carbon nanotubes are presently too short and expensive.  But that’s an engineering issue.  We know we can do it, we just need to work out the details and then get good at it.  In the last 20 years new fabrication techniques have massively increased the yield and dropped the price of nanotubes by a factor of more than 100.  Recently, nanotube “yarn”, made from lots of short bits of nanotube, has demonstrated that it can handle about a third of the theoretical maximum, which is more than good enough for a space elevator (the taper ratio would be, gasp… 4.5ish).

Left: Nanotubes typically aren’t manufactured, they’re “grown” through vapor deposition; you blow hot carbon over this forest, and the atoms that stick, usually stick in the right place.  Right:  But individual nanotubes generally don’t grow to be both flawless and long, so instead they can be gathered up as a kind of yarn with substantially worse performance.  Bottom: That looks like this!

This report for NIAC (NASA Institute for Advanced Concepts and incomplete acronyms) goes through the problems, feasibility, and cost of a space elevator and comes up with a $40 billion price tag for the first elevator and a hell of a lot less for the second.  Budget estimates like this are not the sort of thing that should be taken literally.  “$40 billion” really means “somewhere between $4 and $400 billion”.  The science of reading tea leaves and related sub-fields, like economics, are not great for exact predictions.

So what’s the point?  In short, you personally will never go to the Moon or another planet by rocket.  If you do go, it’ll be by elevator.  Typically when you see a diagram of a space elevator, you see something like the image at the top of this article: Earth, geosynchronous orbit, and a space elevator extending just a little bit beyond it.  But that tail above geosync is worth considering.  Therein fun happens.

A space elevator doesn’t just sedately move material up and down.  If you let go when you’re high enough, it also has the power to fling you across the solar system.

The higher you are the faster you’ll be moving and the less gravity you have to fight against.  A space elevator to 45,000 km gives us access to Earth orbit.  The savings from not needing rockets to put stuff in orbit means the elevator would pay for itself in short order, which is… fine.  On the other hand, an elevator extending out to 200,000 km changes the course of human history.  It gives us immediate and cheap access to and from everything in the solar system.  Our world would go from dangerously small and crowded, to inconceivably vast and resourced in a single generation (unless there’s a reason to drag our feet).  Just for some idea of where we might want to go, there’s likely to be more water on both Enceladus and Europa than on Earth and 16 Psyche is a brick of metallic iron the size of a state, which is especially appealing considering that Earth has zero natural metallic iron (it’s a long, polluting road from iron ore to iron).  Easy access to effectively infinite resources along with plenty of room to grow is a plus.

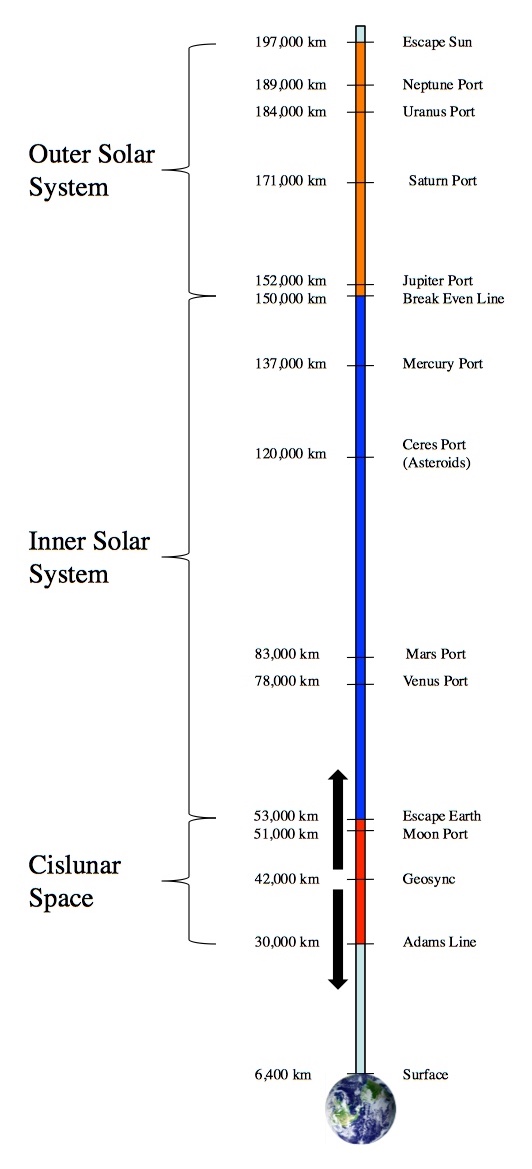
You can build ports to different locations around the solar system at different altitudes along the cable.  Below 30,000 km you’d fall back to Earth.  Between 30,000 and 53,000 km, you’d be in orbit around Earth.  And above 53,000 km, you’d find yourself meandering about the solar system.

If you want to know how to throw a rock that would land on Mars in the least time, using the least energy, the answer is a “Hohmann transfer orbit“.  When you hear about the launch window for Mars only being open once every 780 days (once per synodic period), that’s the window for the Earth-to-Mars Hohmann transfer orbit.  Any other trajectory typically takes longer and requires a lot more rocket power at both ends.

A space elevator is like a sling for space craft and cargo.  By climbing to the appropriate height and letting go during the appropriate launch window, you can go anywhere in the solar system without the need to lift off from Earth or work to escape its gravity.  And the gains in efficiency that come from that are not small.  That whole “rockets need to use fuel to carry their fuel” thing gets out of hand really fast.  Freedom from lift-off means freedom from most of your rocket.

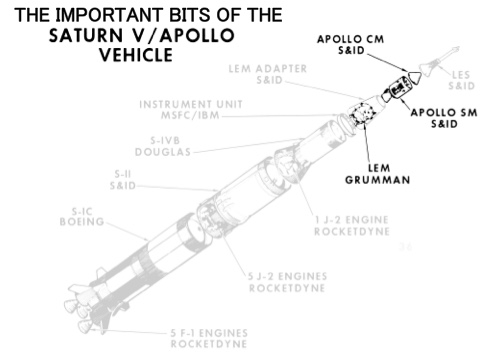
Practically all of every launch vehicle is wasted in the effort to escape Earth’s surface.  This is a problem we can live without.  The greyed-out stuff is everything we could scrap if we felt the need to repeat the Apollo Moon landings using a space elevator.  All that’s left is the equipment for landing on and returning from the Moon (it’s a lot easier to go from there to here).

The Hohmann transfer orbits we use to get to each other planet, are the same ones we’d use to return.  So the “Mars port” is also the best place to catch incoming stuff from Mars.  Asteroid miners wouldn’t have to worry about safely landing cargo on Earth or even slowing it down; they’d just need to aim at the Ceres port and lower it from there.  Earth is about the worst place to build a space elevator, which is why we need nanotubes to do it.  You can easily do the same trick with rotating asteroids to fling stuff back to Earth using cables made from steel and suddenly you’ve got a free ride back home as well.

When designing space elevators, one of the big stumbling blocks often seems to be powering the climber to go up and down.  The consensus seems to be that lasers are a good way to get power to a single climber going in a single direction (electrical cables conduct about as well as wood over tens of thousands of miles).  But that’s very 20th-century-space-thinking.  Consider this: counter weights.

Left: A metallic counter weight for an ordinary elevator.  Right: 21 Lutetia, a source of metallic counter weights for a space elevator (enough to do that Apollo thing 57 trillion times).  With enough counter weight, the energy needed to raise an elevator drops to zero.  In other words, the more resources we ship to Earth, the lower the cost of leaving Earth.

If you’ve ever had the opportunity to look inside an open elevator shaft, you may have noticed that it’s more complicated in there than a single cable attached to the top of the elevator car.  That’s because of the counter weight (and probably safety or something).  The cable coming out of an elevator car goes over a pulley and attaches to a counter weight, so that as the elevator car rises the counter weight falls.  For every 1 kg going down, you get 1 kg going up for free (or nearly free, what with friction).  The same idea can be applied to space elevators.  It takes a lot of power to get a ship up to the Mars port, but if there’s also a ship returning, then everyone gets a much cheaper ride.  If there’s more cargo coming in from the asteroid belt than ships leaving Earth, then suddenly “counter weight tourism” begin to make sense.  Rather than intentionally shedding energy to bring cargo to the ground, you may as well send stuff up.  People, spaceships, garbage, Pog collections, whatever you got.

Almost as good, at 150,000 km, coincidentally between the ports for inner and outer solar system destinations, is the “break even line”.  If you imagine the elevator as “uphill” from the ground to geosync and “downhill” after that, then the break even line is where you’ve gone uphill as much as you’ve gone down hill, so (ignoring friction and assuming the judicious use of counter weights) it takes a total of zero energy to get to the break even line and if you want to go to the outer solar system, there’s a net gain.

At just short of 200,000 km (just over halfway to the Moon) a space elevator can fling stuff into interstellar space, completely clear of the solar system.  While that goes a long way toward traveling to other stars (we don’t have to worry about climbing out of the Sun’s gravity), on its own a space elevator won’t get us moving fast enough to go anywhere outside of the solar system on a even remotely reasonable time scale, if at all.  For example, we recently had an interstellar interloper pass through the inner solar system, ‘Oumuamua.  ‘Oumuamua is a rock traveling at a fairly typical clip of 26 km/s relative to the Sun when it’s in interstellar space.  Unfortunately, to catch up with even this, the closest of all extra-solar objects, we’d need a tether that extends beyond the Moon (out to around 545,000 km).  That presents two problems: first, the taper ratio jumps into the thousands even for nanotubes, and second, the Moon’ll smash the elevator.  Still, “everywhere in the solar system for free” is better than a swift a kick in the pants.

To be clear, the space elevator described above is not crazy science fiction; it’s science fact that just doesn’t happen to exist right now.  Even at the extreme end of the tether you’d experience a maximum of a tenth of Earth’s gravity, so you’re not exactly crushed by centrifugal forces, and the taper ratio never gets above about 2.5.  This is something we can build and comfortably use.  It would be a project on the scale of the Great Wall of China (21,196 km) or the Interstate Highway System (77,556 km), but it’s definitely doable.

Answer Gravy: It may have occurred to you that we live in 3 dimensional space.  That means that places roughly in the plane of the equator are potential targets for a space-elevator-fling, but things above one of the poles are out of reach.  The spin of the Earth keeps it oriented in space, like a gyroscope (well, not like a gyroscope) and that means that if you extend the equator out into space you’ll always hit the same line of stars across the sky, the “celestial equator”.  Everything in the solar system orbits the Sun in roughly the same plane, and since the Earth is included in that plane it appears to us as another line across the sky, “the ecliptic”.  With rare exceptions (mostly things orbiting way out there), everything in our solar system can always be found close to the ecliptic.  These two planes are such important landmarks (spacemarks?) that their intersection is used to define 0° in celestial coordinates; kind of the “Greenwich of the sky”.

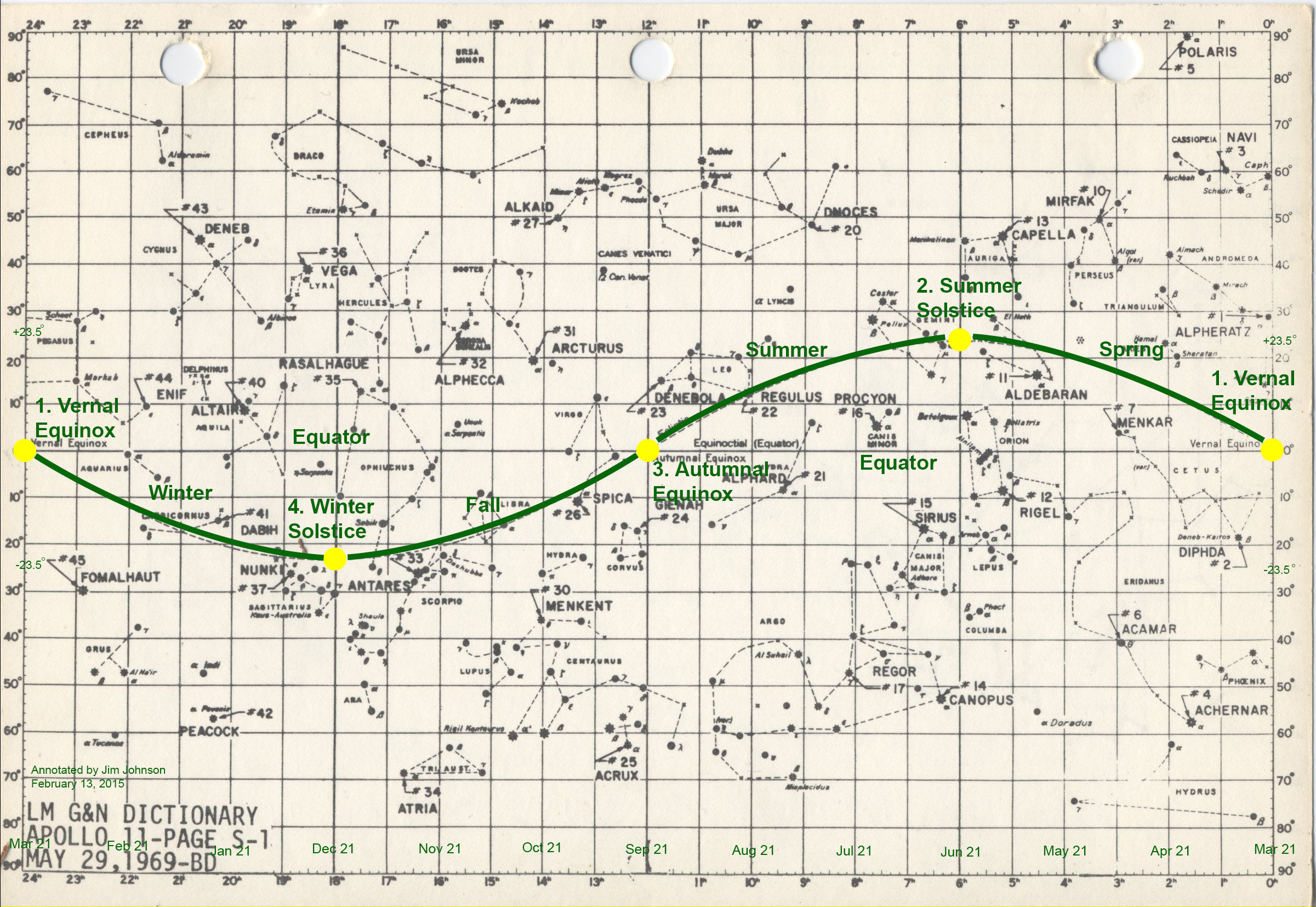
The ecliptic, the (green) path of the Sun and all the planets across the sky, is never more than about 23.5° away from the celestial equator, where an Earth-based space elevator can fling you directly.

So an important question before building a space elevator for the purpose of flinging is “How close are the celestial equator and the ecliptic?”.  It turns out that they’re at most 23.5° apart.  Not coincidentally, this is the Earth’s axial tilt (the ecliptic is what the Earth is tilted with respect to).

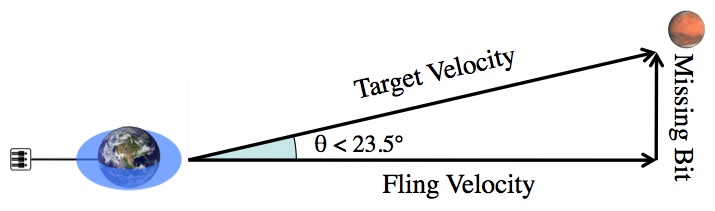
Mars (and basically everything else in the solar system) is on the ecliptic. Earth’s equator, and the arc of any space elevator, is tilted by about 23.5° with respect to the ecliptic.

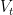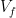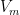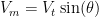If V_t, V_f, and V_m, are the target, fling, and missing velocities and if \theta is the angle between the target velocity and the celestial equator, then by the Pythagorean theorem |V_t|^2=|V_f|^2+|V_m|^2 and by definition V_f=V_t\cos(\theta) and V_m=V_t\sin(\theta).  The total energy the space craft needs is \frac{1}{2}m|V_t|^2=\frac{1}{2}m|V_f|^2+\frac{1}{2}m|V_m|^2, and since \frac{1}{2}m|V_f|^2=\frac{1}{2}m|V_t|^2\cos^2(\theta), the space elevator covers \cos^2(\theta) of the total energy cost.  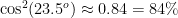That means that in the worst case scenario about \cos^2(23.5^o)\approx0.84=84\% of the energy you need to get where you’re going is free.  Considering that liftoff is no longer a going concern, this is a great opportunity for ion drives (much more efficient, but too weak for liftoff) to pick up the slack.

If you’re wondering how we can tell which materials are worth trying, it comes down to the usual physics process: say something reasonable, say it again with math, watch helplessly as the math spirals out of control, and finally (hopefully) learn something useful.  If the stress on any part of the cable is especially high, then that’s where it’ll snap.  To avoid weak points, we just need the entire cable to be under the same stress.

The total force that a cable can support is the cross-sectional area times the tensile strength (the maximum stress).  This is because two cables can supply twice the force, so the total force must be proportional to the number of cables or (imagine bundling them together) the cross-section.  Every elevation of the cable, r, supports the weight of the entire cable below it.  As you rise up a tiny distance, dr, the cable now has to support the same weight, plus the additional weight of the cable between r and r+dr.  So the additional area, dA, just needs to support the additional weight.

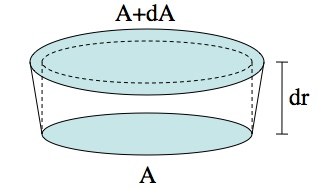
If you rise up a tiny distance, dr, the cable has to expand, dA, to handle the additional weight.

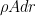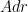Weight is force times mass.  Figuring out the mass is easy: it’s \rho Adr, where \rho is the density of whatever the cable is made of and Adr is area times height, the volume of the “puck”.  It may bother you that by ignoring the dA we’re pretending that the cable isn’t tapering.  This is one of those big advantages of infinitesimals (and calculus in general).  The volume we’re ignoring is \frac{1}{3}dAdr.  dA and dr are “infinitesimals”, meaning that (basically) they’re so small that things start to work out.  As small as they each are, their product, dAdr, is a hell of a lot smaller.  So ignore it.  Things are working out.

“The additional area times the tensile strength is exactly enough to deal with the additional weight” written in mathspeak is

TdA = A\rho dr \left(\underbrace{\frac{gR^2}{r^2}}_{Gravity} - \underbrace{\left(\frac{2\pi}{t}\right)^2r}_{Centrifugal}\right)

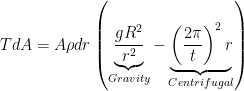
where T is the tensile strength, 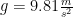g=9.81\frac{m}{s^2} is the acceleration of gravity on Earth’s surface, 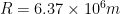R=6.37\times10^6m is the Earth’s radius, and t=8.62\times10^4s is the time it takes Earth to rotate once.  We can simplify this a little by realizing that at the radius of geosync, S=4.22\times10^7m, these two forces are equal

\frac{gR^2}{S^2} = \left(\frac{2\pi}{t}\right)^2S

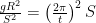
which means we can get rid of π (which is practically a variable, for all you can do with it) and t.  Now: some algebra and calculus.

\begin{array}{rcl} TdA &=& A\rho dr \left(\frac{gR^2}{r^2} - \frac{gR^2r}{S^3}\right) \\[2mm] TdA &=& A\rho gR^2dr \left(\frac{1}{r^2} - \frac{r}{S^3}\right) \\[2mm] \frac{1}{A}dA &=& \frac{\rho gR^2}{T} \left(\frac{1}{r^2} - \frac{r}{S^3}\right)dr \\[2mm] \int\frac{1}{A}dA &=& \int\frac{\rho gR^2}{T} \left(\frac{1}{r^2} - \frac{r}{S^3}\right)dr \\[2mm] \int\frac{1}{A}dA &=& \frac{\rho gR^2}{T}\int \left(\frac{1}{r^2} - \frac{r}{S^3}\right)dr \\[2mm] \ln(A)+C &=& \frac{\rho gR^2}{T}\left(-\frac{1}{r} - \frac{r^2}{2S^3}\right)+C \\[2mm] \ln(A) &=& -\frac{\rho gR^2}{T}\left(\frac{1}{r} + \frac{r^2}{2S^3}\right)+C \\[2mm] A &=& e^{-\frac{\rho gR^2}{T}\left(\frac{1}{r} + \frac{r^2}{2S^3}\right)+C} \\[2mm] A &=& Ce^{-\frac{\rho gR^2}{T}\left(\frac{1}{r} + \frac{r^2}{2S^3}\right)} \\[2mm] \end{array}

Those C’s are constants of integration and, being unspecified numbers, you can do some pretty sloppy math with them: C ± C = C, eC = C, that sort of thing.  If you set that last C to C=e^\frac{3\rho gR^2}{2TS}, then you’ve declared that the cable has a maximum cross-section at geosync of 1 (units TBD).  You can find values for the density and tensile strength of different materials here and you can graph them here, if you want to consider their feasibility for yourself.

Posted in -- By the Physicist, Engineering, Physics | 11 Comments

Q: Could we get rid of CO2 if we pumped it through a pipe into space?

Posted on May 31, 2019 by The Physicist

Physicist: Like any plumbing fix: it depends on the pipe.

Evangelista Torricelli, the first to measure the weight of the air above us, once famously wrote that “Noi viviamo sommersi nel fondo d’un pelago d’aria.” (“We live submerged at the bottom of an ocean of air.”).  That’s a really good way to think about the atmosphere.  It’s held in place around the Earth in exactly the same way that the oceans are held where they are; air has weight and gravity holds it down.  Gravity doesn’t suddenly go away above the atmosphere.  In low Earth orbit (where most satellites can be found) gravity is almost as strong as it is on the surface.  So if you pump air or CO2 or any kind of matter above the Kármán Line (the generally agreed upon, but arbitrary, boundary of space), it will still be subject to gravity and will fall.  You’ll have yourself a CO2 fountain.

Pumping stuff to just above the atmosphere isn’t an effective way to get rid of it, although it might be pretty if it’s visible from the ground.

If you build your pipe straight up from one of the poles, then it’ll be fountain-like even when it’s millions of miles tall.  More importantly, there are no materials that can support such a pipe (it’s important, when building a CO2 pump to the stars, to be realistic).  However, a pipe built up from the equator would swing as the Earth turns, and that changes things a lot.  Shorter pipes (a mere several thousand km tall) will still act like fountains, but eventually that swinging motion becomes important.

Space elevators operate on exactly this idea; combating gravity using the Earth’s rotation.  So figuring out what happens to the CO2 flying out of the top of a very tall pipe boils down to figuring out what would happen if you stepped out of a space elevator at the same height.  And since it is entirely possible (but difficult) to build space elevators, this plan could work.  In fact, since that elevator would need to be made from carbon nanotubes (no other material is known to be strong enough), we’d be using carbon to get rid of carbon.  That’s almost like being efficient!

Douglas Adams once sagely observed that “There is an art to flying, or rather a knack. The knack lies in learning how to throw yourself at the ground and miss. … Clearly, it is this second part, the missing, that presents the difficulties.”  Ordinarily this is difficult, but if the tower you throw yourself off is at least around 30,000 km from the center of the Earth, then by the time you get to the ground it won’t be there.  Sweeping out a larger circle every day than a point on the ground means the platform you jump from will be moving sideways faster.  Once it’s fast enough, when you throw yourself at the ground you’ll literally miss and find yourself in an orbit that skims just above the surface of the Earth at perigee (at the lowest) and returns up to the height of the platform at apogee (at the highest).  Lacking an official name, I do hereby declare this to be the “Adams Line”.

What happens to the CO2 when you pump it into space depends on how high it is when it’s released.

Below the Adams Line, all of the CO2 pumped out of the pipe will fall back to Earth.  Above the Adams line the released CO2 will find itself in orbit, and we’ll have given Earth a ring system.  This wouldn’t be a permanent solution.  All of the material in a ring system needs to “stay in its own lane” and orbit in a near-perfect circle (hence: “ring”) or things will run into each other, lose energy, drop into lower orbits and eventually return to Earth.  A whole series of overlapping elliptical orbits swerving from the height of the pipe to as low as Earth’s surface would be a very messy, very unstable ring system.

Gases released above the Adams Line will orbit the Earth instead of falling back to the ground. However, gases released at different times will be on crossing (colliding) orbits, that would make Earth’s new rings very unstable.

But the higher the pipe, the more circular the orbit.  Once the top of the pipe reaches geosync, it’s in orbit.  If you were to step off of a platform you wouldn’t fall, you’d just drift.  Gas released at this height wouldn’t swerve between altitudes as it orbited Earth, it would more or less stay where it is and instead would slowly fill up the thin ring that forms geosync.  The most expensive and sought-after orbits around Earth would get dirtied up and be far less useful for satellites, but it’s a small price to pay.

We actually have examples of “pipes” releasing gas into their own orbits, so we know more or less what it would look like.  Several of the moons in our solar system are geologically active and, having much lower gravity, eruptions from their surfaces don’t necessarily fall back to the ground.

Enceladus’ ice geysers release water into (roughly) the same orbit around Saturn, forming one of Saturn’s many rings.

 So between the Adams Line and geosynchronous orbit we’d have a temporary ring system, perhaps giving us time to think up an even crazier plan, and above geosync we’d have a fairly stable ring system (no ring systems are entirely stable).  But if we want to get rid of Earth’s CO2 forever, and not just orbitally sequester it, we need it to escape from Earth’s gravity entirely.

At geosync objects orbit Earth once per day.  Below that they orbit faster and above that they orbit slower (for example, the Moon, which is way beyond geosync, takes a month to orbit).  So if the pipe is taller than about 42,000 km, the CO2 it releases will actually fly upward before falling into orbit, and the taller the pipe, the higher that orbit will be.  Beyond about 53,000 km, the top of the pipe will be moving at escape velocity; the CO2 that comes out will fly away from Earth to find its way into orbit around the Sun.

Interesting fun-fact: as measured from the center of any planet, the height of the “Fling Line” is always the cube root of 2 (≈1.26) times the height of geosynchronous orbits.  The Fling Line is a really good goal for anyone planning to build a space elevator, because it’s a free ticket to everywhere.

Swing hard enough and eventually centripetal force wins.  Above the “Fling Line” (not an official name) stuff that’s released never comes back down.

You might worry about some small amount returning to Earth, but you should be equally worried about someone in Antarctica having bad breath; there’s a lot of room for that problem to diffuse.

So that there is the answer.  If you want to solve global warming, you can just gather up and pump CO2 straight up about 53,000 km.  Easy peasy.

The weakness of brilliant plans like this isn’t feasibility (this could technically be done), it’s the naysayers who point out that the cure might be worse than the disease.  After all, carbon is an essential part of the Earth’s biological and chemical systems.  We’ve added about half-again as much CO2 into the atmosphere in the last few centuries, taking us from below 300 ppm to about 400 ppm today.  There’s been 400 ppm of CO2 in the Earth’s atmosphere before now, most recently in the Micene 10 million years ago.  Way back then life on Earth was doing alright (we got grasslands and kelp forests out of it, which isn’t terrible).  Having a bunch of CO2 around isn’t necessarily bad; like highway driving, the danger doesn’t come from any particular situation so much as sudden changes in situation.  Given that, suddenly and irreversibly chucking a third of Earth’s CO2 into space has a fair chance of being a really bad idea.

Answer Gravy: If you’re wondering where the various heights came from, you’ll be thrilled to know that you can figure out the height of both the Adams Line and Fling Line (not the official names), with nothing fancier than algebra.

A Keplerian orbit (a regular elliptical or hyperbolic orbit) can be described as:

r(\theta) = \frac{p}{1+e\cos(\theta)}

where r is the distance from the center of the Earth (or whatever you happen to be orbiting), e is the eccentricity (e=0 for a circle, 0<e<1 for an ellipse), \theta is the angle between the lowest point in the orbit and the present position, and p is (basically) a convenient place holder that determines the overall size of the orbit.

If V_t and V_r are the initial tangential (sideways) and radial (up/down) velocities, h is the initial radius, and \phi is the initial angular position, then you can solve for the orbit using:

\begin{array}{ll}r(\theta) = \frac{(hV_t)^2}{Gm[1+e\cos(\theta)]} \\[2mm]e\cos(\phi) = \frac{hV_t^2}{Gm}-1\\[2mm]e\sin(\phi) = \frac{hV_rV_t}{Gm}\end{array}

Normally you don’t know what the initial angular position is, you just know how high you are and how you’re moving.

This is a slightly streamlined version of the solution that can be found here.  Jumping off of a platform that’s h above the center of the Earth and attached to said Earth means that V_t=\frac{2\pi h}{t}, where t is the length of one sidereal day (the time it takes Earth to fully rotate once).  This is just the distance (the circumference of a large circle, 2πh) over time (one day, t).  Since you’re stepping off of a platform, your initial radial velocity is zero, V_r=0.  Finally, since the question is about the minimum height you could step off such that you would miss the Earth, you’re stepping off at the highest point in the orbit and then dropping, so \phi=180^o.  Normally you need both the second and third equations, but knowing you’re staring at the highest point means you already know what \phi is.  One less equation to worry about!

Use the second equation to solve for e:

\begin{array}{rcl}e\cos(\phi) &=& \frac{rV_t^2}{Gm} - 1 \\[2mm]-e\cos(180^o) &=& \frac{h(\frac{2\pi h}{t})^2}{Gm} - 1 \\[2mm]-e &=& \frac{h(\frac{2\pi h}{t})^2}{Gm} - 1 \\[2mm]e &=& 1 - \frac{h(\frac{2\pi h}{t})^2}{Gm} \\[2mm]e &=& 1 - \frac{4\pi^2 h^3}{Gmt^2} \\[2mm]e &=& \frac{Gmt^2 - 4\pi^2 h^3}{Gmt^2}\end{array}

and then plugging that into the first equation gives us the orbit:

r(\theta) = \frac{(rV_t)^2}{Gm[1+e\cos(\theta)]} = \frac{4\pi^2 h^4}{Gmt^2[1+e\cos(\theta)]}=\frac{4\pi^2 h^4}{Gmt^2[1+\frac{Gmt^2 - 4\pi^2 h^3}{Gmt^2}\cos(\theta)]}=\frac{4\pi^2 h^4}{Gmt^2+(Gmt^2 - 4\pi^2 h^3)\cos(\theta)}

If you plug in \theta = 180^o, you find that the height of the platform is in fact the height of the platform:

r(180^o) = \frac{4\pi^2 h^4}{Gmt^2+(Gmt^2 - 4\pi^2 h^3)\cos(180^o)} = \frac{4\pi^2 h^4}{Gmt^2-(Gmt^2 - 4\pi^2 h^3)} = \frac{4\pi^2 h^4}{4\pi^2 h^3} = h

It’s good to double check.  But to actually figure out what h is (this was the whole point) you want the lowest point in the orbit to be the Earth’s radius, R=6371 km (any lower and you hit the ground).

\begin{array}{rcl}R &=& \frac{4\pi^2 h^4}{Gmt^2+(Gmt^2 - 4\pi^2 h^3)\cos(0^o)} \\[2mm]R &=& \frac{4\pi^2 h^4}{2Gmt^2 - 4\pi^2 h^3} \\[2mm]R(2Gmt^2 - 4\pi^2 h^3) &=& 4\pi^2 h^4 \\[2mm]0 &=& 4\pi^2 h^4 + 4\pi^2 Rh^3 - 2Gmt^2R\end{array}

This is a fourth degree polynomial in h, and while it is technically possible to solve this by hand, you never want to solve this by hand.  So plugging in the gravitational constant, G=6.67\times10^{-11}\frac{m^3}{s^2 kg}, and all of the details about Earth, R=6.37 \times 10^6 m, m=5.97\times 10^24kg, t=86,164s, and then giving this to a computer to solve for you, you find that one of the four solutions makes sense: h=29,825 km.  So if you have to jump into an empty swimming pool, that’s a good height to do it.

The height of the Fling Line (not an official name), f, is a bit easier.  You don’t have to mess around with orbits, you just have to set the speed your platform is moving at a given height, \frac{2\pi f}{t}, equal to the escape velocity at that height, \sqrt{\frac{2Gm}{f}}:

\begin{array}{rcl}\frac{2\pi f}{t}&=&\sqrt{\frac{2Gm}{f}}\\[2mm]\frac{4\pi^2f^2}{t^2}&=&\frac{2Gm}{f}\\[2mm]h^3&=&\frac{2Gmt^2}{4\pi^2}\\[2mm]f&=&\sqrt[3]{\frac{2Gmt^2}{4\pi^2}}\end{array}

You can calculate the height of geosync, s, by setting the centrifugal force equal to the gravitational force for an object orbiting exactly once per (sidereal) day, t:

\begin{array}{rcl} \frac{\left(\frac{2\pi s}{t}\right)^2}{s}&=&\frac{Gm}{s^2}\\[2mm] \frac{4\pi^2s^2}{ht^2}&=&\frac{Gm}{s^2}\\[2mm] s^3&=&\frac{Gmt^2}{4\pi^2}\\[2mm] s&=&\sqrt[3]{\frac{Gmt^2}{4\pi^2}} \end{array}

So that’s a cute, probably useless fact; for any planet, the Fling Line is always at \sqrt[3]{2} times the radius of geosyncronous orbits.

Posted in -- By the Physicist, Engineering, Physics | 37 Comments

Q: Why was it so hard to take a picture of a black hole? What are we even looking at?

Posted on April 14, 2019 by The Physicist

Physicist: Black holes and space are both black, so there’s that.  But while black holes tend to be very small, space is bonkers big and filled with just enough stuff to give astronomers things to look at while simultaneously getting in the way of looking at said things.

The now-famous actual picture of M87* taken in the microwave spectrum.

The picture that you’ve already seen is of M87*, the supermassive black hole (SMB) in the middle of the galaxy M87.  Damn near every galaxy appears to have a SMB in its core.  This isn’t a coincidence, they’re instrumental in the formation of galaxies.  A galaxy’s SMB is almost always dead center and generally has a mass proportionate to the mass of the galaxy it calls home (or more likely, calls “mine”).  Our home galaxy’s supermassive black hole, Sagittarius A*, has the mass of around 4.1 million Suns, which is pretty massive.  But M87* weighs in at around 6.5 billion Suns, more than a thousand times bigger.  M87* is massive even by supermassive standards.

Sagittarius A* is by far the closest SMB (a mere 26,000 light-years away), but of course there’s a galaxy in the way.  To see it we have to look long-ways through the disk of the Milky Way, which is full of stuff.  M87* on the other hand is a freaking monster, but it’s 54 million light-years away.  That’s fairly nearby in galactic terms (you can see it on a dark night), but that’s still incomprehensibly distant.  The light collected to create the picture of M87* was released when our branch on the tree of life was a bunch of tiny, arguably adorable critters, barely recognizable as primates, and expanding across a planet with a recent and notable lack of dinosaurs.  In balance, it was easier to image M87*, a black hole a thousand times bigger and two thousand times farther away, than Sagittarius A*.

As a quick aside, that stunningly boring name, “M87”, comes from Messier (being French, his name is pronounced “mess-E-ay”).  At the time astronomers were getting famous putting their names on comets (worked for Halley) and Messier wanted a part of the action.  It turns out that to an 18th century telescope, there are lots of vague, blurry things in the sky that might be comets, but aren’t.  So Messier wrote a list of things he didn’t want to look at twice, and that rejection list is what he’s remembered for now (incidentally, he also discovered some comets).  The galaxy M87 is the 87th thing on Messier’s “ignore this” list.

Left: The disk of our galaxy (as viewed from inside our galaxy) obscures a band of the sky all the way around us, including the galactic core (home of Sagittarius A*).  Right: As a super giant galaxy, M87 is visible to the naked eye from 54 million light years away.  But as an elliptical galaxy, it looks like a smudge on the lens.  That tiny blue tail is a jet of plasma (one of two) that’s been streaming out of the disk of gas falling into M87* for at least 5000 years.

The blurry doughnut is a cloud of in-falling gases that heat up and ionize as they fall in.  M87*, despite being substantially larger than the orbit of Neptune, is much smaller than the cloud of stuff falling into it, so there’s a bottle neck as gas falls in and that means friction and compression and that means heat.  That glow is a fire storm in space far bigger than our solar system.  The dark in the middle isn’t the black hole itself, so much as a lack of gases.  Newton’s gravity is proportional to the inverse square of the distance to whatever’s making the gravity; half the distance = four times the gravity, a third the distance = nine times the gravity.  In Newton’s gravity, there’s no limit to how close you can be in orbit around something.  But in Einstein’s (correct) formulation of gravity, the inverse square law is only an approximation that works in low gravity situations (basically, Newton is good enough for practically every application except black holes).  It turns out that black holes have an innermost stable orbit, that’s 3 times the Schwarzchild radius (3 times the black hole’s radius).  Anything that tries to orbit closer will just spiral in.  The edge of that doughnut is the innermost stable orbit; the last chance gases have to glow before they get fast-tracked to the black hole itself.

The gas is about the same temperature all the way around M87*, but because it’s spiraling in it’s moving toward us on one side and away on the other.  The side that’s moving toward us appears brighter because of an (usually difficult to notice) effect called “relativistic beaming“; very high speed material emits more light in the direction of motion (although, from its own perspective, it’s still emitting light evenly in every direction).

We were almost guaranteed to see that hot cloud of gas all the way around M87* because, in addition to all the other craziness going on, black holes bend light around them.  This isn’t unique to black holes, we see “gravitational lensing” every time light passes close to something massive.  In fact, one of the earliest confirmations of General Relativity was during the 1919 solar eclipse when stars were seen around the Sun that were actually behind it.  So black holes aren’t the only things that can bend light beams, but they do elevate the art; instead of light being slightly deflected, it can completely change direction or even literally go into orbit.  So when you see a stream of hot gas beside a black hole, it might actually be behind it.  Regardless of how the disk of infalling hot gases are arranged, there will always appear to be gas around the black hole.

Gravitational lensing doesn’t just fun-house-mirror and confuse the image, it actually helps us here.  The dark spot is three times the size of the black hole in reality (the innermost stable orbit), but the lensing effect magnifies it an makes it appear larger.

The gravity of the “red blob” galaxy in the foreground, LRG 3-757, bends the light a galaxy behind it so much that it appears as a ring.  Gravitational lensing like this allows us to measure the distribution of mass by looking at how it warps the image of distant objects, and is sometimes even used intentionally (as a lens!) to get a better view of said distant objects.

The curse of always being right, I’ve been told, is that you’re never surprised and rarely invited to parties.  The new black hole picture isn’t really a discovery, but it is a stunning accomplishment.  Black holes, as we understand them today, were first theorized when Schwarzschild got ahold of the recently published equations of Einstein’s general theory of relativity, applied them to a dense sphere of matter, and followed where they led.  Modern physics has an established track record of starting with basic assumptions, building verifiable theories, and then applying those theories to reach conclusions that everyone agrees are so completely nuts they can’t possibly be true.  Black holes, which are real, are a great example of “so weird they can’t possibly be real”.

Today, you’d have a hard time finding an astronomer or astrophysicist who didn’t already firmly believe in the existence of black holes and their basic, overall properties.  They quibble about the details, sure, but that’s scientists.  There’s a long catalog of observations that already fell in line perfectly with the predicted nature of black holes.  LIGO’s ongoing detections of gravitational waves are beautifully and precisely described by black holes merging.  Stars in the galactic core get whipped back and forth at around 1% the speed of light (which is absurdly fast for anything that isn’t a particle) while orbiting a dark, compact “radio source”.  Quasars, some of the brightest, highest energy things in the universe, are exquisitely described by gases falling into SMBs, but are totally mysterious otherwise.

So what did astronomers expect to see when they finally got a direct image of an actual black hole?  Basically what we’ve seen.  The simulations used to predict what a real picture would look like were disappointingly accurate.

A (non-blurry) image generated by a black hole simulation.

It would have been great if the picture had been completely different.  Like a smiley face or something.  Science advances when we’re wrong or surprised or both.  What this new picture does is add another verification win to the theory of General Relativity, which is good.  It’s not enough to have a clever theory that always works, you also have to give it every possible new opportunity to fail.

So as far as theory goes, we haven’t gained too much.  This was kind of the “eat your vegetables” of empirical physics.  What we gained, we gained through the effort it took to get this picture.  The reason this hasn’t be done before is that it’s really, really hard to do.  M87* is about 54 million light-years away and about 38 billion km across, which makes it 42 microarcseconds across.  There are 360 degrees in a circle, 60 arcminutes in a degree, 60 arcseconds in an arcminute, and a million microarcseconds in an arcsecond.  42 microarcseconds is the angle across a single hair from 500 km away.

But here’s the problem: that’s too small.  There’s a fundamental limit to the resolution of a telescope called the “diffraction limit” that’s built into the wave nature of light.  The more perfectly your telescope is constructed, the closer you can get to this limit, but you can never do better.  If D is the diameter of your telescope’s main lens or mirror and W is the wavelength of the light you’re using, then the smallest angle (in radians) you can resolve is about 1.22\frac{W}{D}, so shorter wavelengths and bigger telescopes produce sharper pictures.  The now-famous black hole image was taken using microwave light with a wavelength of 1.3 mm, which means that to get a fuzzy circle with a dark center (“Hey, a black hole!”) instead of a fuzzy smudge (“Hey, hot gas with maybe a black hole!”) you need a telescope that’s a few thousand km across.  Point of fact: that’s too big.

The Earth happens to be a few thousand km across, so we just need a way to use the whole thing.  Enter the Event Horizon Telescope (EHT), an international collaboration of telescopes that points at M87* with an “effective aperture” that’s about the size of the Earth.  A regular telescope creates images by collecting light and focusing it on a detector.  A light wave from a distant source rolls in like a wall, bounces off of the mirror, and arrives at the focal point all at once.  This is done automatically by the geometry if the mirror is parabolic, since every parallel path takes the same amount of time to get to the focus (that’s just one of those handy properties that parabolas have).

In order to function, a telescope bounces light waves so that they arrive at the detector all at once if they’re coming from the right direction.  Left: In a regular telescope, the shape of the mirror does this automatically.  Right: The Event Horizon Telescope has to put the wave back together using brute force; big computers and ridiculous precision.

If parts of the mirror happens to be missing, that’s fine.  The wave still arrives at the focus all at once, but some of it just passes on through.  So the EHT doesn’t need to cover an area the size of Earth, it just needs to have pieces spread out across the Earth.  But there’s still a huge problem; the light waves rolling in from M87* are never collected at a focal point.  Instead, the data received by each telescope and array is recorded, collected in a single location (often by loading hard drives onto a plane and physically bringing the data together), and processed using a technique called very-long baseline interferometry (VLBI).  “Very-long baseline” refers to the fact that the distance between the individual telescopes is “very long”.  “Interferometry” refers to the fact that the collected light waves need to interfere.

That interference is important; it’s not enough to just report what each telescope sees.  Getting the wave front to arrive at the detector all at once is a really important part of what makes a telescope work.  After all, waves from what you’re not looking at also arrive at your detector, just not all at once.  Parts of the wave arriving at different times interfere destructively and cancel each other out.  So there are two big hurdles: combining the data while also knowing exactly when a given light wave sweeping across Earth arrives at each different telescope’s detector.  You need to be able to tell the difference between one wave front and the next, and if the next wave front is 1.3 mm behind and traveling at the speed of light, then you need to reliably distinguishing between events 4 picoseconds apart (4 trillionths of a second).  So, every telescope needs a shiny new atomic clock and a really fast camera.  You begin to get a sense of why the data consolidation looks more like a cargo shipment than an email attachment; trillions of snapshots every second of not just the waves you’re looking for, but also the waves that will cancel out once all the data is processed.  Add to that the challenge of figuring out (generally after the fact) where every detector is to within a fraction of a millimeter even as their orientation changes and the Earth rotates, and you’ve got a problem.

Or had a problem anyway.  The picture came out just fine.  The two black holes that appear the largest from Earth are Sagittarius A* (because it’s close) and M87* (because it’s a monster), and they’re both right on the edge of what can be effectively imaged using Earth based arrays of telescopes like the EHT.  But if the overarching history of technology is any indication, the first time is almost impossible and the thousandth is embarrassingly easy.  We’ll get better pictures of M87* and passable pictures of Sagittarius A* soon.  Once we set up an array of space telescopes throughout cislunar space (the volume inside the Moon’s orbit) we’ll get pictures of the SMBs in the cores of every nearby galaxy and that’s when the science really gets started.  The cost to low Earth orbit has dropped by 99% since 1980 and the price of spaceflight in general is on schedule to drop substantially more in the decades to come, so a fleet of space telescopes is not such a big ask.

That blurry picture of M87* is the first stumbling steps into a profound new kind of astronomical research that will be totally routine sooner than you think.

The Milky Way picture is from here.

The simulated black hole image is from here.

Posted in Uncategorized | 7 Comments

Q: Will time travel ever be invented?

Posted on March 31, 2019 by The Physicist

Physicist: It already has!  Or rather, it already will be.

Once time travel has/will have been invented, you’d think that said inventor could just go back in time and show off their invention, or give it to some ancestor (or even become some ancestor) so they could be born into old money.

But despite being both common and world-changing, time travel is intrinsically very low-key.  In the 20th century the world population increased from 1.6 to 6 billion people, and even though time travelers account for about 3 of those 4.4 billion new folk, evidence for their presence is almost impossible to find.  It turns out that time machines are just like every other machine; they don’t exist if they’re not invented.  So whatever else anyone does with a time machine, it didn’t/won’t affect the invention of time machines themselves.

In 1992 Steven Hawking derived the “chronology protection conjecture“, which posits that “closed time-like curves” are impossible.  Moving along a time-like path is what you (and every other chunk of matter in the universe) are doing right now; moving slower than light and experiencing time in the usual way.  Moving along a closed time-like path is like going for a walk in the woods and following a trail that returns you home yesterday.  Hawking showed that closed time-like curves produce “feed back” that destroys everything involved.  In other words: Timecop rules.

Ever empirical, on June 28th, 2009 Doc Hawk threw a party for time travelers and (to ensure only time travelers showed up) he kept it secret until June 29th, when he sent out invitations.  Save the date!

To his bemused shock, Hawking’s soiree was very well attended.  He claims to have met “people” from as far afield as 70189324233 AD, the year in which the invitation, as well as the spaciotemporal coordinates of Earth, were unceremoniously overwritten and forgotten during “The Great System Update”.

Left: Steven Hawking, blocking the photographer from getting into the party behind him. Right: The invitation he sent out the next day.  Hope you can/did make it!

At his party, the Hawk discovered three things.  First, time travel is not just possible, but easy.  Second, closed time-like curves are impossible, but that’s not how time travel works.  And third, time travelers don’t leave much evidence behind, because they couldn’t if they tried (and don’t when they do).

Hawking later wrote, “Dear Diary, [I] wasn’t sure about actually buying champagne for the affair, since I knew (or thought I knew) that this was all a [silly stunt].  I’m glad I did!  Time travelers are a cagey lot and the evening didn’t really get into full swing until the 7th or 8th crate was opened.  A man (perhaps?) who introduced himself as the Designate Demithrall of the North Antarctic Seasteader Federation in 4372, mentioned that the key to time travel is my own work on imaginary time and that it’s ‘obvious really, if you think about it’.  This is remarkable!  But in the sober light of da [sic.] I can’t help wondering if the Designate Demithrall wasn’t drunk or sarcastic or both.  Forty-forth century humour is really hard to read.”

When a time traveler intends to give instructions to someone in the past to help them be the first person to build a time machine, they inevitably and accidentally don’t.  The retro-self-cohesion principle of the time-line prevents grandfather paradoxes, so neither time travelers nor machines can change the logic of their own history.  In other words: not Back to the Future rules.  For example, if you go back in time to kill your own grandfather, then you won’t exist to go back in time and do said killing.  You have to come from somewhen.  Inescapably, you’ll either get the wrong guy or fail to get the right guy.  In other words: Bill and Ted rules.  Time travel is possible, and even common, but you can’t change things so much as confirm them.  In the archetypal example, Rufus goes back in time to ensure the Wild Stallions succeed in bringing about peace and enlightenment throughout the universe, and he knows they do because he was/will be there to help.

The “grandfather paradox”. Like all paradoxes, this only shows up on paper.  It can’t happen in reality.

In the same way that you don’t (presently) worry about your murderous unborn grandchildren, the inventor of time travel is immune to hints.  No matter how many time travelers they may incidentally meet, none of them will ever get past general pleasantries; the topic of time travel is logically verboten.  The same holds for common knowledge.  Presumably, the reason that you can’t go online and find the schematics for a (functional) time machine is that the future inventor of time travel doesn’t live in a cave.  The first thing they’re likely to do before getting down to work is a quick internet search to see if they’re reinventing the wheel (or flux capacitor), so all the universe must conspire to make that internet search fail.  Like time travelers themselves, the idea has to come from somewhen.  Being aware of this tautological time travel truth, and possibly having read Hawking’s published diary, the Designate Demithrall was most likely safeguarding the logical consistency (and existence) of the very conversation he was in by filling it with sarcasm and misdirection.

So if you ever meet anyone who claims to be a time traveler and makes no attempt to support their claim, then they’re probably telling you the truth.  Time machines are more common then cellphones, but they’re literally impossible to talk about.  And if you yourself are a time traveler, remember that we ran/will run out of prosecco about halfway through Hawking’s thing, so BYOB.

Posted in -- By the Physicist, April Fools | 16 Comments