Q: What keeps spinning tops upright?

Posted on January 22, 2012 by The Physicist

Physicist: That’s a really tricky question to answer without falling back on angular momentum.  So, without getting into that:

Gyroscopes, tops, and everything that spins are seriously contrarian dudes.  If you try to rotate them in a direction that they’re not already turning, they’ll squirm off in another direction.  When a top starts to fall over it’s being physically rotated by gravity.  But rather than falling, it moves sideways, resulting in “precession“.

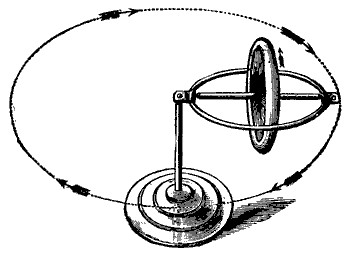
The gyroscope (or top or whatever) spins in one direction, gravity tries to rotate it in a second direction, but it actually ends up turning in the third direction.  Gyroscopes don’t go with gravity (and fall), or even against gravity; they go sideways.

So answering this question boils down to explaining why trying to rotate a gyroscope in a direction it’s not already spinning results in it twisting in the remaining direction.  To picture the mechanics behind spinning stuff, and even to derive the math behind them, physicists think of a spinning object as a bunch of tiny weights tied to each other.  So rather than picturing an entire disk, just picture two weights attached to each other by a thread, spinning.  The circle they trace out defines the “plane of rotation”.  This stuff isn’t complicated, but it is a challenge to picture it in your head all at once, so bear with me.

When you turn something you’re applying “torque“, which is the rotational version of force.  But torque is a little more complicated than plain ol’ force.  In order to turn something you have to push on one side and pull on the other.  When a passing weight experiences a force it changes direction.  Nothing surprising.

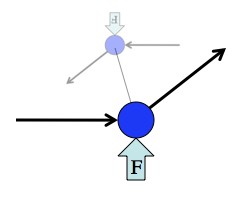
Any spinning object can be thought of as a bunch of small weights spinning around each other. From this perspective the weird behavior of gyroscopes comes closer to making sense.

But when you apply a “push” to one of the weights and a “pull” to the other, you find that that entirely reasonable change in direction causes them both to change direction in such a way that the plane of rotation changes, in a seemingly unreasonable way.

So, say you have a disk on a table in front of you (a record if you’re 30+, a CD if you’re 20 something, or a hard disk if you’re in your teens) and it’s spinning counter-clockwise.  If you grab it and try to “roll it forward”, it will actually pitch left (picture above).

Harder to visualize: in the top picture of this post the gyroscope is turning forward, gravity is trying to pull it to the right, and as a result the gyroscope’s plane of rotation itself rotates.

In the case of actual tops their base if free to move around, instead of just pivoting around a fixed location like in the gyroscope examples so far.  It so happens that if a top starts to fall over the precession of its plane of rotation causes the top to execute a little circle, which it’s leaning into, that, if the top is spinning fast enough, tends to bring the point at its base back under the top (take a look at the gyroscope picture at the top of this post and imagine that it was free to move).  The freedom to move around actually makes tops self-correcting!

On the one hand, that’s great because tops are more fun than bricks and dreidels are more interesting than dice.  On the other hand, the same self-correcting effect (applied to rolling wheels) can cause bikes and motorcycles to keep going long after you’ve fallen off of them.

Answer gravy: The quick and dirty physics explanation is: Angular momentum is conserved and, like regular momentum, that conservation takes the form of both a quantity and a direction.  For example, with regular momentum, two identical cars traveling at 60mph west have equal momentum, but if one of those two identical cars is traveling east at 60mph and the other is traveling west at 60mph, then their momentum is definitely not equal.

For angular momentum you define the “direction” of the angular momentum by curling the fingers of your right hand in the direction of rotation and your thumb points in the direction of the angular momentum vector (this is called the “right hand rule”).  For example, the hands on a clock are spinning, and their angular momentum points into the face of the clock.

The right hand rule.

In order for a top to fall over its angular momentum needs to go from pointing vertically (either up or down, depending on which direction it’s spinning) to pointing sideways.

So, in a cheating nutshell, tops stay upright because falling over violates angular momentum.  Of course, it will eventually fall over due to torque and friction.  The torque (from gravity) creates a greater and greater component of angular momentum pointing horizontally, and the friction slows the top and decreases the vertical component of its angular momentum.  Once the angular momentum vector (which points along the axis of rotation) is horizontal enough the sides of the top will physically touch the ground.

There are some subtleties involving the fact that the “moment of inertia” (which basically takes the place of mass in angular physics) isn’t as simple as a single number.  Essentially, tops prefer to spin on a very particular axis, which makes the whole situation much easier to think about.  However, for centuries creative top makes have been making tops with very strange moments of inertia that causes the tops to flip or drift between preferred axises, which makes for a pretty happening 18th century party.

Posted in -- By the Physicist, Physics | 8 Comments

Q: Do time and distance exist in a completely empty universe?

Posted on January 18, 2012 by The Physicist

Physicist: This is a classic philosophical question!

For a while, it was generally assumed that without matter distance and time would still exist.  After all: why not?  Time is time and space is space, and the material things in them are just “actors on a stage”.  If you remove all the actors, the stage is still there.

That’s not a proof one way or the other, but it does present a salient point: “what’s the damn problem?”

However, that stance took a hit when relativity came along.  First, Galilean relativity, that states that the physics describing how things move around works whether you yourself are moving or not.  His example was someone dropping a stone from the mast of a ship: from the perspective of someone on the ship the stone falls in a straight line (along the mast), and from the perspective of someone on the shore it falls along a curved path.  Both of those people perceive and describe the world exactly as though their “stage” were stationary around them.  Point is; there’s no way to tell whether or not you’re the “correct one” just by chucking rocks about.

Time and space, as seen in Stephen Massicotte’s “The Clockmaker”.  If Galilean relativity starts to sound too complex, keep in mind that it’s just talking about a stage and a clock.

The take-away from Galilean relativity is that, for any pair of events that happen at different times, perspectives moving with respect to each other (boat vs. shore) will see them happen at different relative locations.  Say you’re floating in a void and two firecrackers go off, one after the other.  If you’re moving in the right direction, at the right speed you can “catch” them both and see them both go off right in from of you (it’s important to have protective eye wear in an infinite void).  From most perspectives the firecrackers went off in different places and you had to move to catch them, but from yours, you were stationary and they moved so that they would explode in the same place.

(Left) The firecrackers are sitting still and as the cloudthing whips past they explode.  The explosions are in different places.  (Right) The exact same situation, but with the cloudthing sitting still and the firecrackers exploding (in the same place) as they pass it.  In relativity, there’s no way to tell which is “correct”.  In both diagrams time points in the upward direction.

Still, there’s no problem with there being some particular “stage” with everything in the universe moving around on it.  Heck, the Earth is moving all over the place, but you’d never notice.  The important thing is that a given object will take up a given amount of space (have a set size) that everything can agree on, and will experience the same amount of time as everything else.  In Galilean relativity, the size of objects, the distance between two events that happen at the same time, and time itself are all fixed.  So the dude on the boat and the dude on the shore will always agree on what time it is, as well as how far apart they are at any moment.

The only problem so far is that you can’t tell what’s moving and what’s not.  But there’s nothing to say that somebody out there is standing still.

The issues really start rolling in when you switch over to Einstein’s relativity (also known as “relativity”).  Both Galilean and Einsteinian relativity state that all of physics works the same independent of movement, but Einstein’s relativity includes the added rule “the speed of light is the same to everything, regardless of how that thing is moving”.

That extra rule has a lot of weird consequences that you have to be some kind of Einstein to figure out.

Just like in Galilean relativity, different observers can disagree about where an event can happen, but unlike Galilean relativity, in Einstein’s relativity they can also disagree on when.  Worse than that, the physical size of objects is different, and the duration of events is different, depending on how you’re moving.  You genuinely cannot talk meaningfully about much time or space things “actually” take up.

What you can do, is establish a particular “reference frame”.  Essentially, you measure time and distance from the perspective of some object (one might say “relative” to the object).  In a single reference frame (from the perspective of anything moving at the same speed as the particular object) everything has a size and a position and a time.  The unfortunate thing is that as soon as you look at the same things from a different reference frame, sizes, positions, times, and durations all change.

So finally, to the point.  If there’s nothing at all in the universe to base a reference frame on, then how do you define distance and time?  Keep in mind that you can’t point at a location and say “here” because there’s no you to do the pointing either.  You can easily talk about the size and age of an object in the universe, but the “stage and clock” of the universe itself, on its own, has no particular size or age without something to reference.

Or maybe it does!

Impossible to tell for sure.

The clockmaker image was stolen, without pitty, from http://www.post-gazette.com/pg/10034/1032914-325.stm.

The “cloudthing” is from Hertzfeldt’s opus: Rejected.

Posted in -- By the Physicist, Philosophical, Relativity | 25 Comments

Q: Why is it that photographs of wire mesh things, like window screens and grates, have waves in them?

Posted on January 13, 2012 by The Physicist

Physicist: There are two major effects that generate waves in pictures. The first is called “aliasing”, and it’s caused by “under-sampling”.  It shows up every now and again when you’re using a digital camera, or when you’re trying to express a picture that contains a regular pattern using too few pixels.  The frequency of the pattern is accidentally read as a different frequency.  The second effect is called a Moiré pattern, and it shows up when the camera’s CCD and what the camera is pointed at disagree about what’s horizontal and vertical.  It’s a problem when the lines in question are around 1 or 2 pixels thick.  Technically, in the context of digital cameras, this is just aliasing again.

Moire pattern from two sets of parallel lines.

Normally aliasing is a problem in analog to digital conversion of sound, but it comes up in a number of places.  There’s a theorem called “Nyquist’s theorem” that states that if the highest frequency in a signal or pattern is X, then you need to sample at a frequency of at least 2X or you’ll get aliasing.  In the case of pictures, the smaller the pattern, the higher its “frequency”, and the higher the pixel count the higher the “sampling frequency”.

Aliasing: All three of these waves have the exact same value at 0, 2, 4, etc. so if you're sampling every 2, then they all look the same to you.

For example, most people can hear up to about 22,000 Hz (young people can hear a little higher), so digital recording equipment has to sample sound at least 44,000 times per second (44,000 Hz).  In practice most equipment samples even more.  In this case aliasing causes stray sounds that should be above human hearing to show up in the recording.  Very off-putting.

So, if you have a regular pattern of some kind, like bricks, and you take a picture of it, then in order to avoid weird looking waves, you need at least two pixels per brick.

Left: Under sampled. Right: Sampled enough.

In the picture above the “high-frequency bricks” are aliased and appear to have “low-frequency ripples”.  The effect goes away when you use a zoom lens or a higher resolution, because the sampling frequency increases.

It’s a lot more common to see aliasing show up in digital sound recordings and in video.  The standard 24 frames per second (a sampling frequency of 24 Hz) means that things that repeat faster than 12 times per second will be aliased.  The most jarring example of video aliasing is the “wagon-wheel effect”.  A spinning object on film can appear to be turning at the wrong speed, turning backwards, or even sitting still.  There are some dramatic examples: here and here.

The easiest way to completely avoid aliasing and Moire patterns is to use analog cameras and actual film.  That said, the digital cameras today have such high resolutions that aliasing is pretty unusual.

Answer gravy: So, why do you need to sample at double the frequency, and not just at the frequency?

A wave can be described as x(t)=A\sin{(2\pi ft+\phi)}, where A is the amplitude (size), f is the frequency (how fast it oscillates), and ϕ is the phase (slides the whole thing back and forth).  If all you can do is sample the wave, at times 0,T, 2T, 3T, \cdots (t=nT), then you get a string of values x_0=x(0),x_1=x(T), x_2=x(2T),x_3=x(3T),\cdots.  By definition, the sampling frequency, fs, is 1/T.

So, x_n = A\sin{\left(2\pi f(nT)+\phi\right)}=A\sin{\left(\frac{2\pi}{f_s}nf+\phi\right)}.

But check it: you can add a multiple of 2π inside of sine whenever you want and it doesn’t change anything (sine is “2π periodic“).  So:

\begin{array}{ll}x_n=A\sin{\left(\frac{2\pi}{f_s}nf+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}nf+2\pi nk+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}nf+\frac{2\pi}{f_s}nkf_s+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}n(f+kf_s)+\phi\right)}\end{array}

This means that f \sim f+kf_s.  That is, waves with frequency f, f+fs, f+2fs, etc. will all give you exactly the same set of measurements (xn).  You cannot tell them apart.

But more than that:

\begin{array}{ll}x_n=A\sin{\left(\frac{2\pi}{f_s}nf+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}nf-2\pi nk+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}nf-\frac{2\pi}{f_s}nkf_s+\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}n(f-kf_s)+\phi\right)}\\=-A\sin{\left(\frac{2\pi}{f_s}n(kf_s-f)-\phi\right)}\\=A\sin{\left(\frac{2\pi}{f_s}n(kf_s-f)+\pi-\phi\right)}\end{array}

This type of aliasing is responsible for wheels appearing to spin backward on film.

The “π-ϕ” is different from “ϕ”, however this new phase doesn’t impact the frequency (frequency is what you see and hear).

So, f \sim kf_s-f as well as f \sim kf_s+f.  For succinctness: f \sim kf_s\pm f.

Because of the layout of frequencies that all appear the same (red lines) you can only trust frequencies below half of the sampling frequency, fs.

So check it!  If you have some way to guarantee that the frequency you’re measuring is below \frac{f_s}{2} (using filters or something), then what you see between 0 and \frac{f_s}{2} will be correct.  Otherwise, what you see between 0 and \frac{f_s}{2} may be an alias of a different, higher frequency.

Clearly, most signals aren’t a single frequency the way a sine wave is.  But that doesn’t really matter, since you can write a signal out as a bunch of sine waves added together, and the same math applies to each of those.

Posted in -- By the Physicist, Math | 3 Comments

Q: How does quantum physics affect electron configurations and spectral lines?

Posted on January 8, 2012 by The Physicist

The original question was: I recently got a book about all the chemical elements and noticed how some have a lot of lines of spectra and others hardly any.  I was wondering what exactly causes the lines of spectra to come out the way they do for each element and whether this is related to quantum physics in any way?  Also, I remember learning in Chemistry class that the electrons in an atom absorb energy only at very specific levels and if the energy is not at that level, it doesn’t get absorbed.  I was wondering, how close does the energy level have to match for the electron to accept it – does it have to be completely precise?  And does the electron ever make a mistake so that it somehow only goes up to half an energy level between the orbitals?

Physicist: It’s all about quantum physics!

In fact, the prediction of the position of the spectral lines was one of the first big successes of early quantum physics, specifically the Schrodinger equation.  In general, the larger the atom, the more complex the configuration of electrons you’ll find, and the more spectral lines it’ll have. This is because atomic spectra corresponds to electrons jumping from one configuration to another.  Since each configuration has its own energy level, the transitions always release a very particular amount of energy which for light, means a very particular color or frequency.  Unfortunately, just looking at the spectrum with the naked eye doesn’t tell you as much as you might think.  The vast majority of spectral lines are beyond the range of human vision.

Hydrogen has two charges to worry about and has simple spectral lines. Neon has 11 charges (10 electrons and a bunch of charge in the nucleus) that all interact with each other. This makes neon's spectrum more complex.

The Schrodinger equation describes how electrons (and everything else really) acts like a wave.  Like a wave in a plucked string or a ringing bell, electrons in an atom like to wave at particular frequencies.

But the exact shape (configuration) of the wave function, and thus what frequencies it’s “happy to wave in”, is determined by the electrical forces around the electron/wave.  In a hydrogen atom that’s pretty straight forward: there’s a proton and nothing else.  But in larger atoms there are multiple protons (which doesn’t make too much difference because they’re so close together that they act like one big charge) and multiple other electrons.  This makes the set of available frequencies larger.

A good way to think about this is: if you have a very simply shaped bell it will ring at a very precise frequency (tone, note).  If you have a weird shaped bell, or even something as complicated as a big metal statue, it’ll have more of a “thunk” sound to it.  This is a symptom of the fact that the metal can now vibrate with many different tones (a lot of different ways), instead of one nice clean tone.  Similarly, when there’s a lot going on, the electrons find that they can “wave” in many more complex ways.

Whether or not an electron accepts energy from a photon is pretty complicated.  As a general rule of thumb, the photon’s energy has to be close enough to the possible electron transition energies that the difference can be dealt with using recoil (the left over energy turns into the kinetic energy of the entire atom moving), or “fudged” using the uncertainty principle.

In most solid materials the structure is so irregular, and there are so many ways for electrons and indeed entire atoms to move, that there are far too many energy levels to bother keeping track of.  With so many energy levels available, packed so close together, it’s necessary to start talking about “energy bands”.  Instead of only isolated frequencies being absorbed or emitted, you can see ranges absorbed or emitted.  For example, a substance that appears black probably has an energy band, or set of bands, that covers all of the frequencies in the visible spectrum.

Electrons never transition half-way to other energy levels, but they can exist in a “super-position” of multiple energy levels, which is kinda the next best thing.

Posted in -- By the Physicist, Physics, Quantum Theory | 10 Comments

Q: Is it possible for an atomic orbital to exist beyond the s, p, f and d orbitals they taught about in school? Like could there be a (other letter) orbital beyond that?

Posted on January 4, 2012 by The Physicist

Physicist: There’s no reason for electrons not to fill sub-shells past “f”, it’s just that they don’t need to. By the time the atomic number (which is the number of protons or electrons) is large enough to need a new kind of orbital you’ve got a very unstable element on your hands: element 121, “unbiunium”.

Electrons fill shells in a weird order as the atomic number increases.  A good way to think of the way an electron hangs out around an atomic nucleus is as a “standing wave”.  Thinking of an electron as being like a planet in orbit leads to all kinds of problems.  But while a standing wave on a guitar or cello string is pretty straight forward (take a look), standing waves in two and three dimensions are more complex.  The math behind standing waves in a (symmetrical) 3-d situation is called “spherical harmonics“.

A selection of cross sections of the simplest atomic orbitals.

Most of the energy of an electron’s orbital is determined by what shell it’s in, N=1,2,3…  However, there’s also energy tied up in the weird shapes of the electrons’ sub-shells (denoted by s, p, d, f) and that makes things more complicated than just looking at N.  The math behind calculating the amount of energy for a particular orbital is stunningly nasty.  However, very luckily, the order of orbitals from least energy to most is kinda simple.

Orbitals are arranged by shell (numbers on the left) and orbital shape or "sub-shell" (letters along the bottom).

The “kinda simple” order in which these shells fill up is responsible for the kinda simple structure of the periodic table.  If you feel like tracing it out yourself, these are the basic rules for all of chemistry (relax chemists, your secrets are safe).

The chemical properties of an element are mostly due to the number of electrons in the s and p sub-shells, and the different types hold different numbers of electrons: 2 in s, 6 in p, 10 in d, 14 in f, and so on (increasing by 4 each time).  The lines on the periodic table loop around when the s and p sub-shells are filled.  For example: helium (1s), neon (1s+2s+2p), argon (1s+2s+2p+3s+3p), etc.  The reason that the rows of the periodic table get longer is that the electrons have more sub-shells to fill.

The different "levels" of the periodic table are caused by the strange filling order of the electron orbitals.

The first atom that would need a “g” orbital would be element 121.  However, the largest found so far is 118 (so close!).  For comparison, uranium is element number 92.  This is all a bit of a moot point however.  The higher the atomic number, the less stable the element is.  The half-life of element 118 is about 1/1000 of a second, and 121’s is probably shorter.

Generally speaking, the processes used to create new elements are energetic enough (hot enough) that the atoms are formed in an ionized state.  In order to fill up all of their shells and sub-shells, atoms need to be in a relatively cool environment.  “Cool” as in “colder than plasma”.  So to get an electron to settle into a “g” sub-shell you’d need to create element 121 or higher and then, before all of it radioactively decays into lighter elements (which has a way of ionizing everything nearby), you need to get it cooled off and electrically neutral.  Then, before you can say “Nobel please”, it’s gone.

Posted in -- By the Physicist, Physics, Quantum Theory | 30 Comments

Q: Will the world end in 2012?

Posted on December 31, 2011 by The Physicist

Physicist: Firstly, happy new year!

So, there’s been a lot of hoopla around 2012 doomsday stuff for a while.  Maybe not as much fuss as there was over the techno-apocalypse of Y2K, but still.  Although there are a variety of cited prophecies, the Mayan calender is arguably the most famous.

I’m not knocking them, but if the Mayans could see the future and understood the nature of the universe so very well, then they should have been able to wipe out the conquistadors with their rail guns and bio-weapons, then nuked Spain from their orbital weapons platform, code-named “Ah Chuy Kak“.  That seems like a Mayan response anyway.  Those guys were kinda jerks.

Also, and less interestingly, there’s no evidence that the Mayans even made any 2012 predictions in the first place.

So, dismissing out of hand any claims of prognostication (given that those claims don’t tend to pan out), what is the probability that the world will end in 2012?

20th vs. 21st century soothsaying mostly comes down to a difference in print quality.

Back in the day, a statistician (42% of whom are marginally attractive) named Pierre-Simon Laplace (100% French) considered the question “what is the probability that the sun will rise tomorrow?”.

Like most French, Laplace wasn’t entirely ignorant.  He knew all about the solar system and whatnot.  What he was really getting at was, if you don’t know (or pretend not to know) the underlying probabilities of some phenomena, how do you figure out what those probabilities are?

He figured out that if you see something, that can happen in one of two ways, happen the same way N times in a row, then the probability that it will continue that pattern next time is \frac{N+1}{N+2}.  There’s a generalization to this, but in the case of sunrises, it’s not needed.  Laplace figured, if the Earth is 6 thousand years old (at the time Laplace was living, “young Earth creationist” was essentially the same as “Christian”), then the probability that the sun would rise the next day was around 99.99995%.

One less worry.

Laplace’s “rule of succession“, as the equation is called, assumes a complete lack of knowledge about what the actual probabilities are, but it does require you to know in advance of seeing (or not seeing) an event that either result is possible.

But with the end of the world, we know it’s certainly possible.  We know that the Earth has endured environmental catastrophes that any human survivor (if there were survivors) would call “the end of the world”.  Looking into the solar system we frequently see impact craters of various sizes on objects, ranging from tiny to very-nearly-large-enough-to-blow that-object apart.  (I mean, have you seen Mimas?)  Oddly enough, we never see any that are large-enough-to-blow-that-object-apart.

"Meteor Crater" near Flagstaff, AZ. Sometimes these things happen.

So, could the world end any day now?  Why not.  There’s plenty of stuff that could take us out.

Using only the rule of succession (which basically boils down to “well, it hasn’t happened yet”) we can say that the chance of the entire Earth being destroyed this year is about 1 in 5,000,000,000.

If you define the end of the world as the end of our species, then again using the rule of succession, the probability that we’ll go extinct this year (given no information other than “we’ve made it this far”) is about 1 in 200,000.

It’s kinda comforting to think that the ancient Romans, Mayans, Norse, Indians, freaking everybody, had people running around predicting the end of the world.  Throughout all of known human history there have been people deeply concerned with the impending end of everything and, with any luck, they’ll have a chance to make the rest of us nervous for tens or hundreds of thousands of years to come.

Posted in -- By the Physicist, Paranoia, Probability, Skepticism | 17 Comments