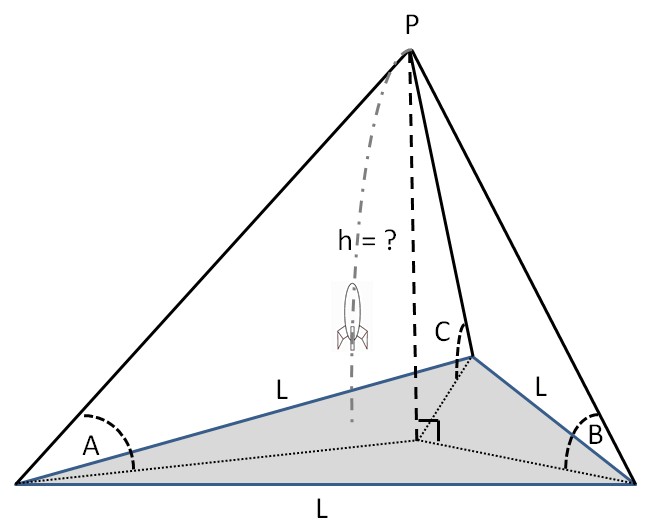
Q: How do you find the height of a rocket using trigonometry?

Posted on December 28, 2011 by The Physicist

The original question was: I am a Physics teacher wanting to measure the height of a rocket.  3 measurers are standing at the corners of an equilateral triangle standing on flat ground.  Each of them measures the angle from horizontal to the highest point of the flight.

The situation.

In other words I want a formula giving the perpendicular height of a point above a horizontal equilateral triangle in terms of the length of side of the triangle and the 3 angles at each corner of the triangle between horizontal and line to the point.  Even better would be a solution where the lengths of the sides of the triangle were not equal.

Physicist: If the rocket doesn’t arch too much, then you can find the maximum height of a rocket by just standing around in a field and measuring the largest angle between the horizon and the rocket.  If somehow you knew the north-south and east-west position of the rocket at the top of its flight, then you’d only need one angle measurement.  But if you don’t know what point on the ground the rocket is above, then things get difficult.

Astrolabes. Fancy name, disappointingly simple device.

In general, if three students (or people in general) are arranged in an equilateral triangle, of side length L, and they measure angles A, B, and C, then the height of the rocket, h, is given by:

h=L\sqrt{\frac{a+b+c\pm\sqrt{6ab+6ac+6bc-3a^2-3b^2-3c^2}}{2(a^2+b^2+c^2-ab-ac-bc)}}

where a=\cot^2{(A)}, b=\cot^2{(B)}, and c=\cot^2{(C)}.

If the bottom of that equation happens to be zero, then rather than everything breaking, you get to use an easier, special-case equation: h = \frac{L}{\sqrt{a+b+c}}.

The advantage of an equilateral triangle is that it’s easy to construct: get three equal lengths of rope, have the three students each take the ends of two ropes, and then walk until the ropes are taught.  The “±” does lend some uncertainty to the measurement, but unfortunately there’s no easy way around it.  Three cones regularly intersect at two points (and solving for the intersection of three cones is pretty much what this is about).  If you can’t disregard one of the answers as ridiculous (like one answer is 5m above the ground, but the rocket clearly went higher), then taking the average of two reasonable answers is easy enough.

Answer gravy: Here’s how you do it (with a little vector math).

The vector that points from the end of vector to another is given by the difference between those vectors, and the angle, θ, between any two vectors can be found using the infamous dot product formula: \vec{V}\cdot\vec{W} = V_1W_1+V_2W_2+V_3W_3 = |\vec{V}||\vec{W}|\cos{(\theta)}.

Say the students are standing at positions \vec{U}, \vec{V}, and \vec{W}.  Then the direction that each student is looking when they look at the rocket is given by \vec{P}-\vec{U}, \vec{P}-\vec{V}, and \vec{P}-\vec{W}.

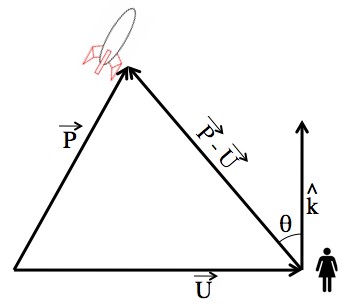
A mess of vectors that describe the relatively simple situation of standing on the ground and looking at a rocket, or up (k).

So, (\vec{P}-\vec{U})\cdot \hat{k} = |\vec{P}-\vec{U}||\hat{k}|\cos{(\theta)}.

But, we’re really interested in the angle from horizontal, A, which is A=90°-θ.  But, cos(θ) = cos(90°-A) = sin(A).  Also, keep in mind that \hat{k}=(0,0,1) and that, since all of the students are on the ground, \vec{U}=(U_1,U_2,0).

\begin{array}{ll}(\vec{P}-\vec{U})\cdot \hat{k} = |\vec{P}-\vec{U}||\hat{k}|\sin{(A)}\\\Rightarrow (P_1-U_1,P_2-U_2,h)\cdot(0,0,1) = |(P_1-U_1,P_2-U_2,h)||(0,0,1)|\sin{(A)}\\\Rightarrow h = |(P_1-U_1,P_2-U_2,h)|\sin{(A)}\\\Rightarrow h^2 = |(P_1-U_1,P_2-U_2,h)|^2\sin^2{(A)}\\\Rightarrow h^2 = \left[(P_1-U_1)^2+(P_2-U_2)^2+h^2\right]\sin^2{(A)}\\\Rightarrow h^2(1-\sin^2{(A)}) = \left[(P_1-U_1)^2+(P_2-U_2)^2\right]\sin^2{(A)}\\\Rightarrow h^2\cos^2{(A)} = \left[(P_1-U_1)^2+(P_2-U_2)^2\right]\sin^2{(A)}\\\Rightarrow h^2\cot^2{(A)} = (P_1-U_1)^2+(P_2-U_2)^2\end{array}

Cleans up nice!  This is just the equation for the student standing at position “U” making measurement “A”.  There are two more, for “V” and “W”:

\begin{array}{ll}h^2\cot^2{(A)} = (P_1-U_1)^2+(P_2-U_2)^2\\h^2\cot^2{(B)} = (P_1-V_1)^2+(P_2-V_2)^2\\h^2\cot^2{(C)} = (P_1-W_1)^2+(P_2-W_2)^2\end{array}

With three equations and three unknowns (P1, P2, and h) there should be enough to solve for h.  You could also solve for P1 and P2, but there’s no point to it.  Solving this problem for arbitrary student positions is horrifying.  But, in the special case of an equilateral triangle it’s not terrible.  \vec{U}=(0,0,0), \vec{V}=(L,0,0), and \vec{W}=(\frac{1}{2}L,\frac{\sqrt{3}}{2}L,0).  So:

\begin{array}{ll}h^2\cot^2{(A)} = P_1^2+P_2^2\\h^2\cot^2{(B)} = (P_1-L)^2+P_2^2\\h^2\cot^2{(C)} = (P_1-\frac{1}{2}L)^2+(P_2-\frac{\sqrt{3}}{2}L)^2\end{array}

After an algebra blizzard, you can finally get t0:

0=(a^2+b^2+c^2-ab-ac-bc)\left(\frac{h}{L}\right)^4-(a+b+c)\left(\frac{h}{L}\right)^2+1

A little quadratic formula, and boom!  You get the equation near the top of this post.  By the way, in the very unlikely event that a^2+b^2+c^2-ab-ac-bc=0, then h = \frac{L}{\sqrt{a+b+c}}.

By the way, it’s easy for errors to creep into this type of measurement, and for middle school students to get, like, way bored.  To avoid both, it may help to have several students at each of the three locations to get redundant measurements.

Posted in -- By the Physicist, Equations, Experiments, Math | 2 Comments

Q: What are chaos and chaos theory? How can you talk about chaos?

Posted on December 22, 2011 by The Physicist

Physicist: Chaos theory, despite what Jurassic Park may lead you to believe, has almost nothing to do with making actual predictions, and is instead concerned with trying to figure out how much we can expect our predictions to suck.

“Pure chaos” is the sort of thing you might want to argue about in some kind of philosophy class, but there are no examples of it in reality.  For example, even if you restrict your idea of chaos to some method of picking a number at random, you find that you can’t get a completely unpredictable number.  There will always be some numbers that are more likely or less likely.  Point is; “pure chaos” and “completely random” aren’t real things.

“Chaos” means something very particular to its isolated and pimply practitioners.  Things like dice rolls or coin flips may be random, but they’re not chaotic.

Dr. Ian Malcolm, shown here distracting a T-rex with a road flare, is one of the few completely accurate depictions of a chaos theorist in modern media.

A chaotic system is one that has well understood dynamics, but that also has strong dependence on its initial conditions.  For example, if you roll a stone down a rocky hill, there’s no mystery behind why it rolls or how it bounces off of things in its path (well established dynamics).  Given enough time, coffee, information, and slide rulers, any physicist would be able to calculate how each impact will affect the course of the tumbling stone.

Although the exact physics may be known, tiny errors compound and trajectories that start similarly end differently.  Chaos!

But there’s the problem: no one can have access to all the information, there’s a diminishing return for putting more time into calculations, and slide rulers haven’t really been in production since the late 70’s.

So, when the stone hits another object on it’s ill-fated roll down the hill, there’s always some error with respect to how/where it hits.  That small error means that the next time it hits the ground there’s even more error, then even more, …  This effect; initially small errors turning into huge errors eventually, is called “the butterfly effect“.  Pretty soon there’s nothing that can meaningfully be said about the stone.  A world stone-chucking expert would have no more to say than “it’ll end up at the bottom of the hill”.

Chaotic systems have known dynamics (we understand the physics), but have a strong dependence on initial conditions.  So, rolling a stone down a hill is chaotic because changing the initial position of the stone can have dramatic consequences for where it lands, and how it gets there.  If you roll two stones side by side they could end up in very different places.

Putting things in orbit around the Earth is not chaotic, because if you were to put things in orbit right next to each other, they’d stay in orbit right next to each other.  Slight differences in initial conditions result in slight differences later on.

The position of the planets, being non-chaotic, can be predicted accurately millennia in advance, and getting more accurate information makes our predictions substantially more accurate.  But, because weather is chaotic, a couple of days is the best we can reasonably do (ever).  Doubling the quality of our information or simulations doesn’t come close to doubling how far into the future we can predict.  Few hours maybe?

Answer gravy: When you’re modeling a system in time you talk about its “trajectory”.  That trajectory can be through a real space, like in the case a stone rolling down a hill or a leaf on a river, or the space can be abstract, like “the space of stock-market prices” or “the space of every possible weather pattern”.  With the rock rolling down the hill you just need to keep track of things like: how fast and in which direction it’s moving, its position, how it’s rotating, that sort of thing.  So, at least 6 variables (3 for position, and 3 for velocity).  As the rock falls down the hill it spits out different values for all 6 variables and traces out a trajectory (if you restrict your attention to just it’s position, it’s easy to actually draw a picture like above).  For something like weather you’d need to keep track of a hell of a lot more.  A good weather simulator can keep track of pressure, temperature, humidity, wind speed and direction, for a dozen layers of atmosphere over every 10 mile square patch of ground on the planet.  So, at least 100,000,000 variables.  You can think of changing weather patterns around the world as slowly tracing out a path through the 100 million dimensional “weather space”.

Chaos theory attempts to describe how quickly trajectories diverge using “Lyapunov exponents“.  Exponents are used because, in general, trajectories diverge exponentially fast (so there’s that).  In a very hand-wavy way, if things are a distance D apart, then in a time-step they’ll be Dh apart.  In another time-step they’ll be (Dh)h = Dh2 apart.  Then Dh3, then Dh4, and so on.  Exponential!

Because mathematicians love the number e so damn much that they want to marry it and have dozens of smaller e’s (eeeeeeee), they write the distance between trajectories as D(t) = D_0e^{\lambda t}, where D(t) is the separation between (very nearby) trajectories at time t, and D0 is the initial separation.  \lambda is the Lyapunov exponent.  Generally, at about the same time that trajectories are no longer diverging exponentially (which is when Lyapunov exponents become useless) the predicting power of the model goes to crap, and it doesn’t matter anyway.

Notice that if \lambda is negative, then the separation between trajectories will actually decrease.  This is another pretty good definition of chaos: a positive Lyapunov exponent.

λ < 0. Pick two points that are close together, then run time forward. They get closer.

A beautiful, and more importantly fairly simple, example of chaos is the “Logistic map”.  You start with the function f(x) = rx(1-x), pick any initial point x_0 between 0 and 1, then feed that into f(x).  Then take what you get out, and feed it back in.  That is; x1 = f(x0), x2 = f(x1), …  This is written “recursively” as “x_{n+1}=rx_n(1-x_n)“.  The reason this is a good model to toy around with is that you can change r and get wildly different behaviors.

For 0<r<1, xn converges to 0, regardless of the initial value, x0.  So, nearby initial conditions just get closer together, and \lambda <0.

For 1<r<3, xn converges to one point (specifically,\frac{r-1}{r}), regardless of x0.  So, again, \lambda <0.

For 3<r<3.57, xn oscillates between several values.  But still, regardless of the initial condition, the values of xn still settle into the same set or values (same “trajectory”).

But, for 3.57<r, xn just bounces around and never converges to any particular value.  When you pick two initial values close to each other, they stay close for a while, but soon end up bouncing between completely unrelated values (their trajectories diverge, exponentially).  The is the “chaotic regime”.  \lambda >0.

(bottom) Many iterations of the logistic map for r = 3.30 (2 value region) and r = 3.9 (chaotic region).  (middle) The values that Xn converge to, regardless of Xo, for various values of r.  The blue lines correspond to the examples.  (top) Lyapunov exponent of the Logistic map for various values of r. Notice that the value is always zero or negative until the system becomes chaotic.

Long story short, chaos theory is the study of how long you should trust what your computer simulations say before you should start ignoring them.

Posted in -- By the Physicist, Math, Probability | 11 Comments

Q: What is the Riemann Hypothesis? Why is it so important?

Posted on December 17, 2011 by The Physicist

Physicist: To non-mathematicians this seems like a whole lot of fuss over nothing.

There’s a function called the Riemann Zeta function, denoted “\zeta (s)“, that’s defined for complex numbers (that is, you can plug in i for example, and it’s totally fine).  The Riemann hypothesis is a statement about where \zeta (s) is equal to zero.  On its own, the locations of the zeros are pretty unimportant.  However, there are a lot of theorems in number theory that are important (mostly about prime numbers) that rely on properties of \zeta (s), including where it is and isn’t zero.

For example the prime number theorem, which talks about yet another greek-letter-named function, \pi (x).  \pi (x) is defined as the number of primes less than or equal to x.  So, for example, \pi (6) = 3 (2, 3, and 5 are prime and less than 6).  \pi (x) is a lot more useful than it might seem at first blush.  We unfortunately can’t give an explicit equation for \pi (x), but the Riemann hypothesis is instrumental in proving the efficacy of techniques that estimate it efficiently and (fairly) well.

Lest you think primes are unimportant; many organizations, including the NSA, snatch up every number theorist they can get, to do research on this sort of stuff.  Since the late 70’s they’ve even been trying to classify mathematical proofs, or declare certain algorithms to be “munitions”, so that they can’t be written down and taken over-seas.  This, by the way, is unheard of in mathematical and scientific circles.  Mathematicians and computer scientists, being a cantankerous bunch (I mean, have you seen their WoW characters?), have by and large refused to play along.

Prime-number-math has really come into its own in the last several decades, what with digital stuff looking less and less like a passing fad.  For example, cell phones (which are like regular telephones, but with fewer wires), essentially wouldn’t work without spread spectrum communication (to cut down on noise) and “quadratic residue sequences” (to eliminate cross-talk) which relies on some properties of primes to allow multiple digital signals to work on the same frequency band!  Good times!

Answer gravy: \zeta (s) is really weirdly defined.  When it makes sense to do so, for example when s>1, it’s defined as \zeta (s)=\sum_{n=1}^\infty \left(\frac{1}{n}\right)^s=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\frac{1}{5^s}+\frac{1}{6^s}+\cdots

Where s can be any complex number.  How can you raise things to complex (imaginary) powers?  Good question!

Quick aside: Complex numbers are generally written as A+Bi, where i is the square root of -1.  Since there are two numbers in complex numbers (hence the name) you can’t have a “number line”, you need a plane, which is called the “complex plane”.  The “real part” of A+Bi is the part that doesn’t have an i, and the “imaginary part” is the part that does.  So if s=-5+3i, then Re(s)=-5 and Im(s)=3.

The summation form above “makes sense” when the real part of s is greater than 1, and as the analytic continuation of that sum when the real part is less than or equal to 1.  For those values the sum can be torn apart and put back together (mathematically speaking) in a new, terrifying form that works everywhere: \zeta (s) = \frac{1}{1-2^{1-s}}\sum_{n=0}^{\infty} \left(\frac{1}{2}\right)^{n+1} \sum_{k=0}^n (-1)^k {n \choose k} (k+1)^{-s}.

\zeta (s) has a lot of places where it’s value is zero.  Firstly at every negative even number: \zeta (-2)=\zeta (-4)=\zeta (-6)=\cdots =0.  These are called the “trivial zeros” because it’s trivially easy* to prove that they’re there.

There are also other zeros called the “non-trivial zeros” that extend on, or very near, a line perpendicular to the real numbers.  In fact, the statement of the Riemann hypothesis can be expressed as: “if s is a non-trivial zero of \zeta (s), then Re(s)=1/2″.  So, the hypothesis is that all of the non-trivial zeros are exactly on the line defined by Re(s)=1/2.

The absolute value of the Riemann Zeta function for a range of values in the complex plane. Zeta explodes to infinity at s=1 and is zero when s is an even negative integer. The Riemann hypothesis is that all of the other zeros lay on the dotted line, Re(s)=1/2.

It has been proven that there an infinite number of non-trivial zeros.  Of the ten trillion (give or take) found so far, all of them seem to have a real part of exactly 1/2.

Given that evidence, most mathematicians think the Riemann hypothesis is true.  But trillions of confirmations do not a proof make.

One way to get some idea of why \zeta(s) is related to prime numbers (and thus, why the Riemann hypothesis in related to primes) is to re-write \zeta (s) in the form of an infinite product, instead of an infinite sum:

\zeta (s) =\underset{primes}{\prod} \frac{1}{1-p^{-s}}=\frac{1}{1-2^{-s}}\cdot\frac{1}{1-3^{-s}}\cdot\frac{1}{1-5^{-s}}\cdot\frac{1}{1-7^{-s}}\cdot\frac{1}{1-11^{-s}}\cdots

Each term is just 1/(1-p^{-s}), where p steps through every prime (2,3,5,7,11,13,…).  The product form and the summation form are the same because of the unique factorization theorem, and a little algebra.

In general, \frac{1}{1-x} = 1+x+x^2+x^3+\cdots, when |x|<1.  And, since \frac{1}{p}<1, \frac{1}{1-1/p}=1+\frac{1}{p}+\frac{1}{p^2}+\frac{1}{p^3}+\cdots.  When you multiply these sequences you get every possible combination of terms.  For example, \left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots\right)\left(1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\cdots\right) will give you 1/6, 1/12, 1/8, … anything  of the form 1/2n3k.  Similarly, multiplying by every sequence of primes will give you every possible combination of primes and powers of primes which is just another way of saying “all integers”.  \begin{array}{ll}\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{10}+\cdots \\=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{2^2}+\frac{1}{5}+\frac{1}{2\cdot 3}+\frac{1}{7}+\frac{1}{2^3}+\frac{1}{3^2}+\frac{1}{2\cdot 5}+\cdots\end{array}

Mixing a power of “s” in there doesn’t make a difference to the derivation, but it does clutter up the notation.

*It’s not really that easy.

Posted in -- By the Physicist, Equations, Math, Number Theory | 12 Comments

Twitter

Posted on December 13, 2011 by The Physicist

Holy crap!  Ask a Mathematician / Ask a Physicist now has a twitter account: @AAMAAP

It’ll be used to announce new posts and whatnot.

Posted in Uncategorized | 3 Comments

Q: Why does the entropy of the universe always increase, and what is the heat death of the universe?

Posted on December 13, 2011 by The Physicist

Physicist: The increase of entropy is just how a scientist talks about the fact that the universe tends to do the most likely thing.  For example, if you throw a bucket of dice you’ll find that about a sixth of them will be 1, about a sixth will be 2, and so on.  This has the most ways of happening, so it’s the most likely outcome, and for the same reason it’s the outcome with the highest entropy.

High entropy.  Arrangements of lots of dice tend, over time, to end up like this.

In contrast, you wouldn’t expect all of the dice to be 4 at the same time, or otherwise assume one particular pattern.  That would be a very unlikely and low entropy outcome.

Audrey Hepburn is one of the lower entropy states you’ll find.  Or rather, will never find, because it’s so unlikely.  You have to sit back and squint a little to see it.

“Entropy” is just a mathematical tool for extending the idea down to atomic interactions, where we don’t have a nice idea like “dice” to work with.

One of the things that increasing entropy does is to spread out heat as much as possible.  If you have a hot object next to a cold object, then the heat will spread so that the cooler object heats up, and the hotter object cools down, until the two are at the same temperature.  The idea (the math) behind that is the same as the idea behind mixing fluids or sands together.  There are more ways for things to be mixed than sorted.

The same thing happens on a much larger scale.  The Sun, and every other star, is radiating heat into the universe.  But they can’t do it forever.  Eventually the heat will have spread out so much that there won’t be warmer objects and cooler objects.  Everything will be the same temperature.  The same, very cold, temperature.  The vast majority of the universe is already screaming cold, so the heat death of the universe is just about burning what fuel there is and mixing the heat so created into the ever-expansive, cold, and unyielding cosmos.  Both the burning of fuel (mostly through fusion in stars) and the distribution of heat are processes which increase entropy.

The cold and unyielding cosmos. What’s the stupid point of anything?

Once everything is the same temperature, the universe attains a “steady state”.  With no energy differences, there’s no reason for anything to change what it’s doing (all forces can be expressed as an energy imbalance or “potential gradient“).  Heat death is the point at which the universe has finally settled down completely (or almost completely), and nothing interesting ever happens again.

Which is depressing, but it is a fantastically long time away.  There are a hell of a lot of other bad things that’ll probably happen first.

The eminent philosophers Flanders and Swann have a more up beat take on the heat death of the universe:

“Heat is work, and work’s a curse,

and all the heat in the universe,

is gonna cool down.  ‘Cause it can’t increase,

then there’ll be no more work, and there’ll be perfect peace.

That’s entropy, man.”

Posted in -- By the Physicist, Entropy/Information, Physics | 61 Comments

Q: Could God have existed forever? Is it actually feasibly possibly for some ‘being’ to have just existed, infinitely?

Posted on December 10, 2011 by The Physicist

Physicist: Far be it for me to tell a god what it can do.

Without knowing more about the exact properties of gods, there’s not much to work with.  The best way to answer this is to get a few thousand gods, and see if they last forever. If most or all of them do, then there’s a good chance that any particular god/being could last forever.  This kind of eternity-based science requires some patience.

Some experiments seem to take forever, and some really do (or would).

Unfortunately, the two tricks at a scientist’s disposal are observation and experiment.  Even logic and inference have to step aside for experimental results (or more precisely, the assumptions that the logic is based on has to step aside).  And there have been times when our “obvious” base assumptions, like “absolute time” (time is the same for everything) or the “geocentric hypothesis” (we’re totally not being flung around space at thousands of miles per hour), have been beaten down by overwhelming evidence.  But gods (at least the god of the gaps) don’t seem to be observable.

I’m sure you’ve noticed that very few things seem to last forever (games of Risk, Iron Maiden, etc).  Those things that we know of that have lasted, intact, the 13 or so billions years since the universe began tend to be very simple, like individual protons.  As for things that existed “before the universe” (even assuming that makes any physical sense), nothing can be said at all.  If it’s not in the universe, then it can’t be observed or experimented with and, scientifically speaking, that means we’re s.o.l.

Posted in -- By the Physicist, Philosophical | 21 Comments