Physicist: “Spin” or sometimes “nuclear spin” or “intrinsic spin” is the quantum version of angular momentum. Unlike regular angular momentum, spin has nothing to do with actual spinning.
Normally angular momentum takes the form of an object’s tendency to continue rotating at a particular rate. Conservation of regular, in-a-straight-line momentum is often described as “an object in motion stays in motion, and an object at rest stays at rest”, conservation of angular momentum is often described as “an object that’s rotating stays rotating, and an object that’s not rotating keeps not rotating”.
Any sane person thinking about angular momentum is thinking about rotation. However, at the atomic scale you start to find some strange, contradictory results, and intuition becomes about as useful as a pogo stick in a chess game. Here’s the idea behind one of the impossibilities:
Anytime you take a current and run it in a loop or, equivalently, take an electrically charged object and spin it, you get a magnetic field. This magnetic field takes the usual, bar-magnet-looking form, with a north pole and a south pole. There’s a glut of detail on that over here.
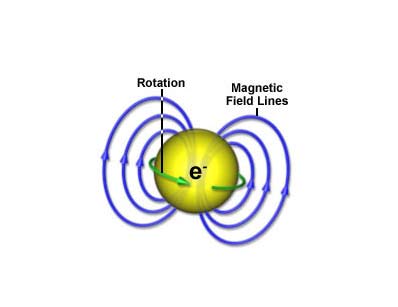
A spinning charged object carries charge in circles, which is just another way of describing a current loop. Current loops create “dipole” magnetic fields.
If you know how the charge is distributed in an object, and you know how fast that object is spinning, you can figure out how strong the magnetic field is. But in general, more charge and more speed means more magnetism. Happily, you can also back-solve: for a given size, magnetic field, and electric charge, you can figure out the minimum speed that something must be spinning.
It’s not too hard to find the magnetic field of electrons, as well as their size and electric charge. Btw, these experiments are among the prettiest experiments anywhere. Suck on that biology!
Electrons do each have a magnetic field (called the “magnetic moment” for some damn-fool reason), as do protons and neutrons. If enough of them “agree” and line up with each other you get a ferromagnetic material, or as most people call them: “regular magnets”.
Herein lies the problem. For the charge and size of electrons in particular, their magnetic field is way too high. They’d need to be spinning faster than the speed of light in order to produce the fields we see. As fans of the physics are no doubt already aware: faster-than-light = no. And yet, they definitely have the angular momentum necessary to create their fields.
It seems strange to abandon the idea of rotation when talking about angular momentum, but there it is. Somehow particles have angular momentum, in almost every important sense, even acting like a gyroscope, but without doing all of the usual rotating. Instead, a particle’s angular momentum is just another property that it has, like charge or mass. Physicists use the word “spin” or “intrinsic spin” to distinguish the angular momentum that particles “just kinda have” from the regular angular momentum of physically rotating things.
Spin (for reasons that are horrible, but will be included anyway in the answer gravy below) can take on values like 
where 
(“h bar“) is a physical constant. This by the way, is a big part of where “quantum mechanics” gets its name. A “quantum” is the smallest unit of something and, as it happens, there is a smallest unit of angular momentum (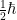
)!
It may very well be that intrinsic spin is actually more fundamental than the form of rotation we’re used to. The spin of a particle has a very real effect on what happens when it’s physically rotated around another, identical particle. When you rotate two particles so that they change places you find that their quantum wave function is affected. Without going into too much detail, for particles called fermions this leads to the “Pauli Exclusion principle” which is responsible for matter not being allowed to be in the same state (which includes place) at the same time. For all other particles, which are known as “bosons”, it has no effect at all.
Answer gravy: Word of warning; this answer gravy is pretty thick. A familiarity with vectors, and linear algebra would go a long way.
Not everything in the world commutes. That is, AB≠BA. In order to talk about how badly things don’t commute physicists (and other “scientists”) use commutators. The commutator of A and B is written “[A,B] = AB-BA”. When A and B don’t commute, then [A,B]≠0.
As it happens, the position measure in a particular direction, Rj, doesn’t commute with the momentum measure in the same direction, Pj (“j” can be the x, y, or z directions). That is to say, it matters which you do first. This is more popularly talked about in terms of the “uncertainty principle“. On the other hand, momentum and position measurements in different directions commute no problem.
For example, ![[R_x,P_x]=i\hbar](https://s0.wp.com/latex.php?latex=%5BR_x%2CP_x%5D%3Di%5Chbar&bg=ffffff&fg=000000&s=0 "[R_x,P_x]=i\hbar")
and ![[R_x,P_y]=0](https://s0.wp.com/latex.php?latex=%5BR_x%2CP_y%5D%3D0&bg=ffffff&fg=000000&s=0 "[R_x,P_y]=0")
. This is more succinctly written as ![[R_j,P_k]=i\hbar \delta_{jk}](https://s0.wp.com/latex.php?latex=%5BR_j%2CP_k%5D%3Di%5Chbar+%5Cdelta_%7Bjk%7D&bg=ffffff&fg=000000&s=0 "[R_j,P_k]=i\hbar \delta_{jk}")
, where 
This is the “position/momentum canonical commutation relation“.
In both classical and quantum physics the angular momentum is given by 
. This essentially describes angular momentum as the momentum of something (
) at the end of a lever arm (
). Classically and are the position and momentum of a thing. Quantum mechanically they’re measurements applied to the quantum state of a thing.
For “convenience”, define the “angular momentum operator”,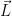 
, as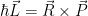 
or equivalently 
, where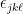 
is the “alternating symbol“. This is just a more brute force way of writing the cross product.
Now check this out! (the following uses identities from here and here)
![\begin{array}{ll}\hbar^2[L_j,L_k]\\=[\hbar L_j,\hbar L_k]\\=\left[\sum_{st}\epsilon_{stj}\vec{R}_s\vec{P}_t, \sum_{mn}\epsilon_{mnk}\vec{R}_m\vec{P}_n\right]\\=\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\left[\vec{R}_s\vec{P}_t,\vec{R}_m\vec{P}_n\right]\\=\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\left(\left[\vec{P}_t,\vec{R}_m\right]\vec{R}_s\vec{P}_n+\left[\vec{P}_t,\vec{P}_n\right]\vec{R}_s\vec{R}_m+\left[\vec{R}_s,\vec{R}_m\right]\vec{P}_t\vec{P}_n+\left[\vec{R}_s,\vec{P}_n\right]\vec{P}_t\vec{R}_m\right)\\=\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\left(-i\hbar\delta_{tm}\vec{R}_s\vec{P}_n+0+0+i\hbar\delta_{sn}\vec{P}_t\vec{R}_m\right)\\=i\hbar\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\left(\delta_{sn}\vec{P}_t\vec{R}_m-\delta_{tm}\vec{R}_s\vec{P}_n\right)\\=i\hbar\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\delta_{sn}\vec{R}_m\vec{P}_t-i\hbar\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\delta_{tm}\vec{R}_s\vec{P}_n\\=i\hbar\sum_{stm}\sum_n\epsilon_{stj}\epsilon_{mnk}\delta_{sn}\vec{R}_m\vec{P}_t-i\hbar\sum_{stn}\sum_m\epsilon_{stj}\epsilon_{mnk}\delta_{tm}\vec{R}_s\vec{P}_n\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D%5Chbar%5E2%5BL_j%2CL_k%5D%5C%5C%3D%5B%5Chbar+L_j%2C%5Chbar+L_k%5D%5C%5C%3D%5Cleft%5B%5Csum_%7Bst%7D%5Cepsilon_%7Bstj%7D%5Cvec%7BR%7D_s%5Cvec%7BP%7D_t%2C+%5Csum_%7Bmn%7D%5Cepsilon_%7Bmnk%7D%5Cvec%7BR%7D_m%5Cvec%7BP%7D_n%5Cright%5D%5C%5C%3D%5Csum_%7Bstmn%7D%5Cepsilon_%7Bstj%7D%5Cepsilon_%7Bmnk%7D%5Cleft%5B%5Cvec%7BR%7D_s%5Cvec%7BP%7D_t%2C%5Cvec%7BR%7D_m%5Cvec%7BP%7D_n%5Cright%5D%5C%5C%3D%5Csum_%7Bstmn%7D%5Cepsilon_%7Bstj%7D%5Cepsilon_%7Bmnk%7D%5Cleft%28%5Cleft%5B%5Cvec%7BP%7D_t%2C%5Cvec%7BR%7D_m%5Cright%5D%5Cvec%7BR%7D_s%5Cvec%7BP%7D_n%2B%5Cleft%5B%5Cvec%7BP%7D_t%2C%5Cvec%7BP%7D_n%5Cright%5D%5Cvec%7BR%7D_s%5Cvec%7BR%7D_m%2B%5Cleft%5B%5Cvec%7BR%7D_s%2C%5Cvec%7BR%7D_m%5Cright%5D%5Cvec%7BP%7D_t%5Cvec%7BP%7D_n%2B%5Cleft%5B%5Cvec%7BR%7D_s%2C%5Cvec%7BP%7D_n%5Cright%5D%5Cvec%7BP%7D_t%5Cvec%7BR%7D_m%5Cright%29%5C%5C%3D%5Csum_%7Bstmn%7D%5Cepsilon_%7Bstj%7D%5Cepsilon_%7Bmnk%7D%5Cleft%28-i%5Chbar%5Cdelta_%7Btm%7D%5Cvec%7BR%7D_s%5Cvec%7BP%7D_n%2B0%2B0%2Bi%5Chbar%5Cdelta_%7Bsn%7D%5Cvec%7BP%7D_t%5Cvec%7BR%7D_m%5Cright%29%5C%5C%3Di%5Chbar%5Csum_%7Bstmn%7D%5Cepsilon_%7Bstj%7D%5Cepsilon_%7Bmnk%7D%5Cleft%28%5Cdelta_%7Bsn%7D%5Cvec%7BP%7D_t%5Cvec%7BR%7D_m-%5Cdelta_%7Btm%7D%5Cvec%7BR%7D_s%5Cvec%7BP%7D_n%5Cright%29%5C%5C%3Di%5Chbar%5Csum_%7Bstmn%7D%5Cepsilon_%7Bstj%7D%5Cepsilon_%7Bmnk%7D%5Cdelta_%7Bsn%7D%5Cvec%7BR%7D_m%5Cvec%7BP%7D_t-i%5Chbar%5Csum_%7Bstmn%7D%5Cepsilon_%7Bstj%7D%5Cepsilon_%7Bmnk%7D%5Cdelta_%7Btm%7D%5Cvec%7BR%7D_s%5Cvec%7BP%7D_n%5C%5C%3Di%5Chbar%5Csum_%7Bstm%7D%5Csum_n%5Cepsilon_%7Bstj%7D%5Cepsilon_%7Bmnk%7D%5Cdelta_%7Bsn%7D%5Cvec%7BR%7D_m%5Cvec%7BP%7D_t-i%5Chbar%5Csum_%7Bstn%7D%5Csum_m%5Cepsilon_%7Bstj%7D%5Cepsilon_%7Bmnk%7D%5Cdelta_%7Btm%7D%5Cvec%7BR%7D_s%5Cvec%7BP%7D_n%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=0 "\begin{array}{ll}\hbar^2[L_j,L_k]\\=[\hbar L_j,\hbar L_k]\\=\left[\sum_{st}\epsilon_{stj}\vec{R}_s\vec{P}_t, \sum_{mn}\epsilon_{mnk}\vec{R}_m\vec{P}_n\right]\\=\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\left[\vec{R}_s\vec{P}_t,\vec{R}_m\vec{P}_n\right]\\=\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\left(\left[\vec{P}_t,\vec{R}_m\right]\vec{R}_s\vec{P}_n+\left[\vec{P}_t,\vec{P}_n\right]\vec{R}_s\vec{R}_m+\left[\vec{R}_s,\vec{R}_m\right]\vec{P}_t\vec{P}_n+\left[\vec{R}_s,\vec{P}_n\right]\vec{P}_t\vec{R}_m\right)\\=\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\left(-i\hbar\delta_{tm}\vec{R}_s\vec{P}_n+0+0+i\hbar\delta_{sn}\vec{P}_t\vec{R}_m\right)\\=i\hbar\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\left(\delta_{sn}\vec{P}_t\vec{R}_m-\delta_{tm}\vec{R}_s\vec{P}_n\right)\\=i\hbar\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\delta_{sn}\vec{R}_m\vec{P}_t-i\hbar\sum_{stmn}\epsilon_{stj}\epsilon_{mnk}\delta_{tm}\vec{R}_s\vec{P}_n\\=i\hbar\sum_{stm}\sum_n\epsilon_{stj}\epsilon_{mnk}\delta_{sn}\vec{R}_m\vec{P}_t-i\hbar\sum_{stn}\sum_m\epsilon_{stj}\epsilon_{mnk}\delta_{tm}\vec{R}_s\vec{P}_n\end{array}")
Therefore: ![[L_j,L_k]=i\epsilon_{jk\ell}L_{\ell}](https://s0.wp.com/latex.php?latex=%5BL_j%2CL_k%5D%3Di%5Cepsilon_%7Bjk%5Cell%7DL_%7B%5Cell%7D&bg=ffffff&fg=000000&s=0 "[L_j,L_k]=i\epsilon_{jk\ell}L_{\ell}")
.
So what was the point of all that? It creates a relationship between the angular momentum in any one direction, and the angular momenta in the other two. Surprisingly, this allows you to create a “ladder operator” that steps the total angular momentum in a direction up or down, in quantized steps. Here are the operators that raise and lower the angular momentum in the z direction:
Notice that
![\begin{array}{ll}[L_z,L_+]\\=[L_z,L_x\pm iL_y]\\=[L_z,L_x]\pm i[L_z,L_y]\\=iL_y\pm i(-iL_x)\\=iL_y\pm L_x\\=\pm(L_x \pm iL_y)\\=\pm L_\pm\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D%5BL_z%2CL_%2B%5D%5C%5C%3D%5BL_z%2CL_x%5Cpm+iL_y%5D%5C%5C%3D%5BL_z%2CL_x%5D%5Cpm+i%5BL_z%2CL_y%5D%5C%5C%3DiL_y%5Cpm+i%28-iL_x%29%5C%5C%3DiL_y%5Cpm+L_x%5C%5C%3D%5Cpm%28L_x+%5Cpm+iL_y%29%5C%5C%3D%5Cpm+L_%5Cpm%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=0 "\begin{array}{ll}[L_z,L_+]\\=[L_z,L_x\pm iL_y]\\=[L_z,L_x]\pm i[L_z,L_y]\\=iL_y\pm i(-iL_x)\\=iL_y\pm L_x\\=\pm(L_x \pm iL_y)\\=\pm L_\pm\end{array}")
Here’s how we know they work. Remember that Li is a measurement of the angular momentum in the “j” direction (any one of x, y, or z). For the purpose of making the math slicker, the value of the angular momentum is the eigenvalue of the L operator. If you’ve made it this far; this is where the linear algebra kicks in.
Define the “eigenstates” of Lz, 
, as those states such that 
. “m” is the amount of angular momentum (well… “
” is), and is defined as the state that has that amount of angular momentum. Now take a look at what (for example)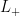 
does to :
![\begin{array}{ll}L_zL_+|m\rangle\\=\left(L_zL_+-L_+L_z+L_+L_z\right)|m\rangle\\=\left([L_z,L_+]+L_+L_z\right)|m\rangle\\=[L_z,L_+]|m\rangle+L_+L_z|m\rangle\\=L_+|m\rangle+L_+L_z|m\rangle\\=L_+|m\rangle+mL_+|m\rangle\\=(1+m)L_+|m\rangle\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7DL_zL_%2B%7Cm%5Crangle%5C%5C%3D%5Cleft%28L_zL_%2B-L_%2BL_z%2BL_%2BL_z%5Cright%29%7Cm%5Crangle%5C%5C%3D%5Cleft%28%5BL_z%2CL_%2B%5D%2BL_%2BL_z%5Cright%29%7Cm%5Crangle%5C%5C%3D%5BL_z%2CL_%2B%5D%7Cm%5Crangle%2BL_%2BL_z%7Cm%5Crangle%5C%5C%3DL_%2B%7Cm%5Crangle%2BL_%2BL_z%7Cm%5Crangle%5C%5C%3DL_%2B%7Cm%5Crangle%2BmL_%2B%7Cm%5Crangle%5C%5C%3D%281%2Bm%29L_%2B%7Cm%5Crangle%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=0 "\begin{array}{ll}L_zL_+|m\rangle\\=\left(L_zL_+-L_+L_z+L_+L_z\right)|m\rangle\\=\left([L_z,L_+]+L_+L_z\right)|m\rangle\\=[L_z,L_+]|m\rangle+L_+L_z|m\rangle\\=L_+|m\rangle+L_+L_z|m\rangle\\=L_+|m\rangle+mL_+|m\rangle\\=(1+m)L_+|m\rangle\end{array}")
Holy crap! 
is an eigenstate of 
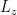with eigenvalue 1+m. This is because, in fact, 
!
Assuming that there’s a maximum angular momentum in any particular direction, say “j”, then the states range from 
to 
in integer steps (using the raising and lowering operators). That’s just because the universe doesn’t care about the difference between the z and the negative z directions. So, the difference between j and negative j is some integer: j-(-j) = 2j = “some integer”. For ease of math the were separated from the L’s in the definition. The actual angular momentum is “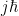
“.
By the way, notice that at no point has mass been mentioned! This result applies to anything and everything. Particles, groups of particles, your mom, whatevs!
So, the maximum or minimum angular momentum is always some multiple of half an integer. When it’s an integer (0, 1, 2, …) you’ve got a boson, and when it’s not (1/2, 3/2, …) you’ve got a fermion. Each of these types of particles have their own wildly different properties. Most famously, fermions can’t be in the same state as other fermions (this leads to the “solidness” of ordinary matter), while bosons can (which is why light can pass through itself).
Notice that the entire ladder operator thing for any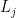 
is dependent on the L operators for the other two directions. In three or more dimensions you have access to at least two other directions, so the argument holds and particles in 3 or more dimensions are always fermions or bosons.
In two dimensions there aren’t enough other directions to create the ladder operators (
). It turns out that without that restriction particles in two dimensions can assume any spin value (not just integer and half-integer). These particles are called “anyons”, as in “any spin”. While actual 2-d particles can’t be created in our jerkwad 3-d space, we can create tiny electromagnetic vortices in highly constrained, flat sheets of plasma that have all of the weird spin properties of anyons. As much as that sounds like sci-fi, s’not.
It’s one of the several proposed quantum computer architectures that’s been shown to work (small scale).
.
.
.
.
.
, for the event B. Then, our formula reads:
.
