Q: What’s the difference between black holes and worm holes? Could black holes take you to other universes?

Posted on October 18, 2011 by The Physicist

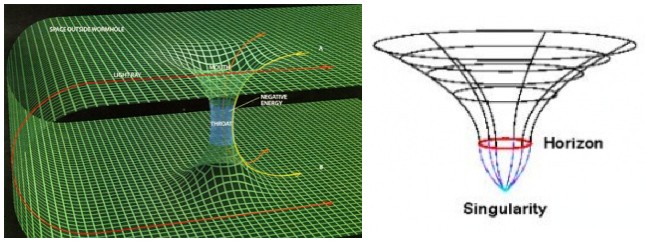
Physicist: The short answer is: A worm hole is a “tube made of spacetime” that connects two different regions.  If it’s set up right, you could enter one side of the tube and exit the other end somewhere else, or even somewhen else.  In contrast, a black hole destroys the hell out of things, and doesn’t “go anywhere”.

A worm hole is a funnel (what’s shown here is only a two dimensional funnel) that tapers down to a “throat” (which although thinner never pinches off entirely) which connects to another funnel that opens up somewhere else.  A black hole is a funnel that pinches off at a singularity.  A traversable worm hole needs to be large and “mellow” enough that it doesn’t have an event horizon (a black hole’s “point of no return”), or any fatal tidal forces.

The hand-wavy idea behind worm holes (left) vs. black holes (right).

There’s a long history of the two being mixed up.  For example, there are a number of stunningly bad movies that make the connection between black holes and worm holes explicit.  But even in legitimate (non-Hollywood) physics circles you’ll sometimes find people talking about “going through” black holes, as opposed to (or in addition to) “being destroyed a lot” by black holes.

Over the years physicists have gotten a little gun shy about ignoring solutions.  For example, one of the clearly impossible solutions to the Schrodinger equation (which describes the wave nature of things) involves particles crossing through impossible boundaries.  Turns out they can, and it’s now called “quantum tunneling“.  In fact, you probably even own some electronic devices that take advantage of this “impossible” solution!

Another example is when Dirac took the Schrodinger equation and re-wrote it in a relativistic form to create the Dirac equation (the original equation isn’t compatible with relativity).  He found that he suddenly had a second set of solutions which imply the existence of anti-particles.  At the time the idea of an anti-particle was ridiculous, but a few years later positrons (anti-electrons) were discovered and Dirac was shown to be right.

So, given the history, physicists today are a little hesitant about chucking out solutions, even when they’re silly.  And black holes are a bottomless pit of math with solutions that seem impossible.

The singularity at the center of a black hole is usually described as a point.  However, this is a symptom of our paltry computational power back when black holes were first being theoretically researched.  A singularity can actually take a number of forms.  According to a variety of (modern/powerful) computer models, as a star collapses to form a black hole it often finds itself forming “singularity sheets” in areas where its density becomes large enough.  All of it ends up in the same tiny singularity moments later, but it’s still interesting.  In a spinning black hole (which is all of them, to some extent or another) the singularity takes the form of a “ring singularity”, which is exactly what it sounds like.

One of the wild things about ring singularities is that they make the topology of spacetime qualitatively different, in a way not entirely dissimilar to the way that the surface of a sphere is qualitatively different from the surface of a doughnut (or, for our New York readers, a bagel).

In normal, everyday space, if you travel in a big loop you come back to the same place.  If you were a mathematician you would prove this using a “continuous deformation”.

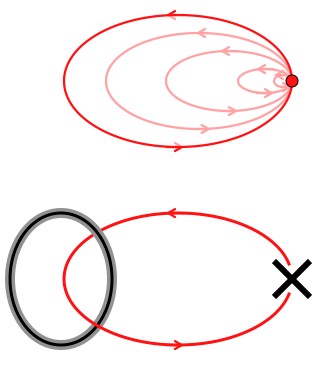
In ordinary space moving in a loop has the same net effect as not moving. But if your loop takes you through a ring singularity, that may not be the case.

A big loop is nearly the same as a slightly smaller loop, is nearly the same as a slightly smaller loop, is nearly the same… is nearly the same as a point.  If there’s a singularity in the way the loop that goes around it can’t be smoothly deformed into a loop that doesn’t.  As a result, traveling on a path that takes you through a ring singularity doesn’t necessarily need to bring you back to where you expected to be.

As hand wavy and weird as this idea sounds, it has a lot of mathematical relevance.  It shows up all the time in complex integrals and branch cuts, and just a hell of a lot in algebraic topology.  But, to be fair, nobody’s ever seen a physical “doorway through space and time” kind of example.

Beyond just the singularity, there are a lot of weird problems involving picturing how black holes work.  For example, they screw up spacetime so much that at their surface (the “event horizon”) time literally points downward.  Not only do you have to contend with the fact that spacetime is four dimensional (3 space directions plus 1 time direction), but the time direction is very different, so it’s four dimensional in a really weird way.  Now add to that that black holes royally mess things up and you’ll find yourself in dire need of a better coordinate system to make things easier to picture.

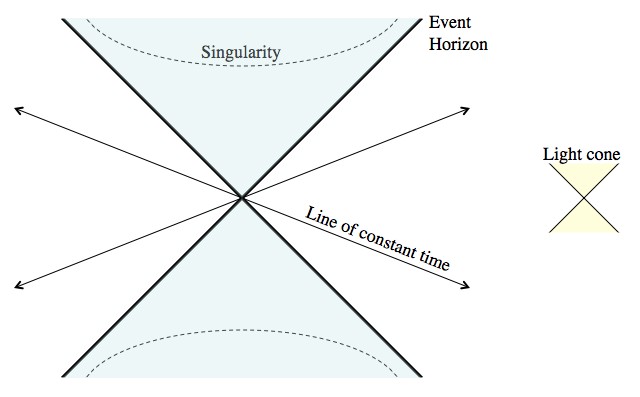
A black hole in K-S coordinates.  Light travels at a 45° angle everywhere in this diagram, which physicists like, but everything else is weird.

Enter Kruskal–Szekeres coordinates.  Although the situation is still a little weird, time points more or less up (the standard set up for space/time diagrams), and light travels diagonally (again: standard).  In these coordinates all of our universe is on the right side, including all of the past and future, the event horizon of the black hole is the upper diagonal (and, oddly enough, the infinite future), and the singularity is a sweeping curve in the top area.  Keep in mind that this coordinate system is more than a little bit weird.  For example, they assume that the black hole exists forever (into the past and future) at the same size.  So the bottom diagonal is an unashamed representation of the infinite past.  Any finite time in the past (say, the beginning of the universe) would be slightly above the lower diagonal.

Now the point: you can write down a lot of the physics of general relativity in these coordinates and they look pretty good, so it feels like there’s something to them.  However, they include a left side.  General relativity treats the stuff on the left the same way it treats everything on the right (our universe).  So, if the left is something more than just a mathematical artifact, then it’s another space and time completely independent from our own.  Since nothing travels faster than light, which in these coordinates travels along diagonals, it’s impossible to get from any point in our universe to the other universe.  However, if you fall into the black hole you can see someone from the other universe that’s also fallen into the balck hole, and have a nice chat before you’re both destroyed at the singularity.

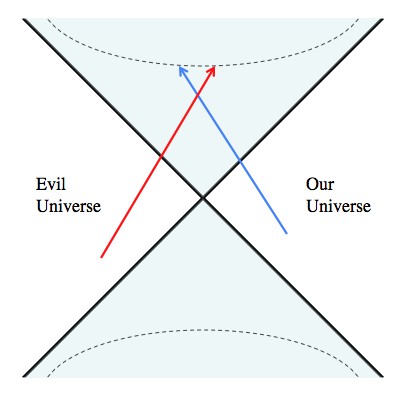
Although you’d need to travel faster than light to get from one universe to the next (if the next exists), you can meet other doomed travelers from the next universe without traveling faster than light.  The upside is making new friends.  The downside is being destroyed in a black hole.

If faster than light travel were possible, and if there were another spacetime on the other side of the black hole that wasn’t just a mathematical convenience or ring singularities behave exactly like we want them too, and if you could make it into and out of the black hole without being destroyed a lot or taking forever doing it (it takes literally forever to fall past the event horizon), then black holes are certainly doorways to other universes, or different parts of our own.

So, to the point, there’s a history of people confusing or blurring the distinction between black holes and worm holes, and not completely without reason, but in general: black holes mean stop and worm holes mean go.

Posted in -- By the Physicist, Astronomy, Math, Physics, Relativity | 36 Comments

Q: Is there an equation that determines whether a question gets answered on ask a mathematician/physicist?

Posted on October 13, 2011 by The Mathematician

Mathematician: Yes, but neither the Physicist nor I know it, and its shortest representation in standard mathematical notation is much too long to ever be written down. More precisely, there are an infinite number of such equations. These equations “exist” in the same sense that an equation describing the current position of every hair on your head exists. But these equations do not exist in the same sense that Chicago exists.

 

Posted in -- By the Mathematician, Philosophical | 8 Comments

Q: If you could hear through space as though it were filled with air, what would you hear?

Posted on October 9, 2011 by The Physicist

Physicist: You’d be able to hear the Sun, and nothing else.  Maybe at night you’d be able to hear your own thoughts.

Owing to the nature of how things like sound and light spread out, the loudness and brightness of a thing is exactly proportional to how big it appears.

The amount of light we get from the Sun is a function of its temperature (around 5,500 °C) and the angle it takes up in the sky (about half a degree across).

If you could get a small metal ball to the same temperature (assuming it wouldn’t melt, which is exactly what it would do) and moved it so that it appeared to be the same size as the Sun (0.5 degrees) then it would feel exactly as warm and bright as the Sun feels from here (on Earth).

As you move away from a source the intensity of that source drops like 1/R^2, simply because the energy gets spread out over a larger area.  And, as you move away from a source, the size that the source appears to shrink the same way.  This is a useful “math hack” to figure out how big things would need to be to look/sound the same.

Similarly, the Sun, if we could hear it, would be exactly as loud as any other large-marble-sized nuclear explosion held at arm’s length.

Quite loud.

There are some issues with the nature of sound.  Notably, if sound gets too loud it stops acting like a wave and tends to break apart.  It stops acting like sound and starts to act more like a frothy foam of shock fronts.

But as long as we’re hearing through space, we may as well ignore that problem too.

Posted in -- By the Physicist, Astronomy, Physics | 11 Comments

Q: What is the three body problem?

Posted on October 3, 2011 by The Physicist

Physicist: The three body problem is to exactly solve for the motions of three (or more) bodies interacting through an inverse square force (which includes gravitational and electrical attraction).

The problem with the 3-body problem is that it can’t be done, except in a very small set of frankly goofy scenarios (like identical planets following identical orbits).

The unsolvableness of the 3-body problem, rather than being an embarrassing hole in physics, an obvious but unsolved problem, is actually the norm.  In physics, the number of not-baby-simple, exactly solvable problems can be counted on the fingers of one hand (that’s missing some fingers), and that includes the 2-body problem.

The dynamics of one body is pretty straight forward, in as much as it travels straight forward.

The dynamics of two bodies, while not trivial, can be reduced by pretending that one body is sitting still, and then restricting all of your attention to the other body.  Using that technique, you find (or, at least, Newton found) that the motion of a body under gravity is an ellipse.  The same idea can be applied to the quantum mechanics of electrons and protons to find the exact structure of the electron shells in hydrogen (1 proton + 1 electron = 2 bodies).  In that case you’re not talking about actual orbits, but the idea is similar.

But, for three bodies, there doesn’t seem to be a fancy trick for finding solutions.  As a result, the exact behavior of 3 or more bodies can’t be written down.  The exact energy levels and orbital shell shapes in anything other than hydrogen is impossible to find.  Even deuterium (hydrogen with one extra neutron)!  Can’t be done.

Despite that, we do alright, and happily, reality doesn’t concern itself with doing math, it just kinda “does”.  For example, quantum field theory, despite being the most accurate theory that ever there was, never involves exactly solving anything.  Once a physicist gets a hold of all the appropriate equations and a big computer, they can start approximating things.  With enough computing power and time, these approximations can be made amazingly good.  Computer simulation and approximation is a whole science unto itself.

But even with just mechanical pencil and paper there are cheats.  For example, although there are more than three bodies in the solar system (the Sun, eight planets, dozens of moons, and millions of asteroids and comets), almost everything behaves, roughly, as though it were in a two body system.  Basically, this is due to the pronounced size differences between things.  As far as each planet is concerned, the only important body in the rest of the universe is the Sun.  To get some idea of why; the Sun pulls on the Earth about 200 times harder than the Moon, and about 20,000 times harder than Jupiter.  Nothing else even deserves a mention.  So, if you want to calculate the orbits of all the planets, a “2-body approximation” will get you more than 99% of the way to the right answer.

But that last 1% has a lot of weirdness in it, most of which falls out of chaos theory.  The more interesting part of chaos theory is the “islands of stability”, or what we in the biz call “chaotic attractors”.  While you find that no real life N-body system orbits are stable (exactly repeat themselves), you do find that they settle into patterns.  For example, while the system of Jupiter’s innermost moons: Io, Europa, and Ganymede, never quite repeats the same path, they do manage to “resonate” with each other and settle into a rhythm.  Hence the name; “orbital resonance“.

Basically, when you have several bodies orbiting a much larger body, the length of the orbits of the smaller bodies will tend to settle into simple-fraction (1/2, 2/3, 1/3, etc.) multiples of each other.  1 to 2 to 4 for Io, Europa, and Ganymede.  The slight ellipses of any real-life orbits cause the gravitational force of the moons, to “pulse” (becoming slightly stronger or weaker) along another moon’s orbit.  As a result (this is not at all obvious right off the bat) if the other moon slows down it gets pushed a little faster at regular intervals, and if it gets too fast it gets slowed down at regular intervals.

The moons still have very elliptical orbits (a symptom of being in a 2-body system with Jupiter), but the presence of the other moons does affect how big that ellipse is, and in what direction it “points”.

When you have even more bodies you can almost abandon the idea that there are any bodies at all, and move over to fluid dynamics.  Although, again, that’s just an approximation.

(upper left) The 2-body Earth/Moon system as seen from one of those bodies.  (upper right) The 5-body Jupiter/Galilean-moons system as seen with binoculars.  (bottom) The more-than-a-few-body Andromeda system as seen with some kind of big-ass telescope.

Point is, this effect only shows up in systems with three or more bodies, it’s chaotic (in the chaos theory sense), and there is no way to predict it exactly.  That being said, we can still get computers to come pretty close (up to a point, because chaos is a punk), and there are even some mathematical tricks to get reasonable solutions that, while not perfect, are still pretty good (and can even get us well into that last “1% of weirdness”).

Answer gravy: First, this is how to solve the gravitational two body problem.

Take two masses, M_1 and M_2, with positions given by \vec{P}_1 and \vec{P}_2.  Then the force on M_1 (keep in mind that F=MA) is given by Newton’s law of gravitation:

M_1 \ddot{\vec{P}}_1 = -\frac{GM_1M_2}{|\vec{P}_1-\vec{P}_2|^3}\left( \vec{P}_1-\vec{P}_2\right)

Where “\vec{P}_1-\vec{P}_2” is the vector that points from \vec{P}_2 to \vec{P}_1, and the double-dots on the left hand side indicates the second time derivative (which is math speak for acceleration).

If it bothers you that the bottom of the right side is cubed (not squared), it’s because this is a vector equation that includes both the magnitude of the force and the its direction.  If you look at just the magnitude of both sides you get M_1 \left| \ddot{\vec{P}}_1 \right| = \frac{GM_1M_2}{|\vec{P}_1-\vec{P}_2|^3}\left| \vec{P}_1-\vec{P}_2\right|= \frac{GM_1M_2}{|\vec{P}_1-\vec{P}_2|^2}.

Now, since for every action there’s an equal, but opposite reaction (every force is balanced by another force):

M_2 \ddot{\vec{P}}_2 = -M_1 \ddot{\vec{P}}_1

Now check this out!

\begin{array}{ll}\ddot{\vec{P}}_1-\ddot{\vec{P}}_2\\=\ddot{\vec{P}}_1-\frac{M_2}{M_2}\ddot{\vec{P}}_2\\=\ddot{\vec{P}}_1 +\frac{M_1}{M_2} \ddot{\vec{P}}_1 & \left(because\quad M_2 \ddot{\vec{P}}_2 = -M_1 \ddot{\vec{P}}_1\right)\\=\left(1 +\frac{M_1}{M_2}\right) \ddot{\vec{P}}_1 \\=\left(1 +\frac{M_1}{M_2}\right) \frac{M_1}{M_1} \ddot{\vec{P}}_1 \\= -\left(1 +\frac{M_1}{M_2}\right) \frac{1}{M_1} \frac{GM_1M_2}{|\vec{P}_1-\vec{P}_2|^3}\left( \vec{P}_1-\vec{P}_2\right) & \left(because\quad M_1 \ddot{\vec{P}}_1 = -\frac{GM_1M_2}{|\vec{P}_1-\vec{P}_2|^3}\left( \vec{P}_1-\vec{P}_2\right) \right)\\= -\left(1 +\frac{M_1}{M_2}\right) \frac{GM_2}{|\vec{P}_1-\vec{P}_2|^3}\left( \vec{P}_1-\vec{P}_2\right)\\= -\left(M_2 +M_1\right) \frac{G}{|\vec{P}_1-\vec{P}_2|^3}\left( \vec{P}_1-\vec{P}_2\right)\\= -\frac{G(M_1 +M_2)}{|\vec{P}_1-\vec{P}_2|^3}\left( \vec{P}_1-\vec{P}_2\right)\\\end{array}

At this point just replace “\vec{P}_1-\vec{P}_2” with “\vec{x}“, and “M_1 +M_2” with “M“.

\ddot{\vec{x}} = -\frac{GM\vec{x}}{|\vec{x}|^3}

Then jump over the the elliptic orbit post to find the ellipticalness of this.  The subtle, unspoken assumption of that post is that the Sun doesn’t move (i.e., it was already stated in the “reduced form”).  Which is exactly what this math has been setting up.  “\vec{P}_1-\vec{P}_2” is called “the relative position vector”, and all it does is point from the second body to the first body.  So describing its dynamics is the same as describing the dynamics of a world where the second body is stationary.

So here’s the tough part.

In the 2-body problem all you have to worry about is the attraction between body 1 and body 2.  In the 3-body problem there are 3 attraction terms to worry about.  In the 4-body there are 6, in the 5-body there are 10, etc. (in general there are \frac{N(N-1)}{2} terms for N bodies, which gets bad fast)

The ease of the one attraction term in the 2-body problem vs. the horror of the 10 attraction terms in the 5-body problem.  Readers are invited to note that 5 isn’t even that big a number.

In the 3-body problem, in order to find the total force on body 1, body 2, and body 3 you have to add the attraction from each of the other bodies:

\begin{array}{ll}M_1 \ddot{\vec{P_1}} = -\frac{GM_1M_2}{|\vec{P}_1-\vec{P}_2|^3}\left( \vec{P}_1-\vec{P}_2\right) -\frac{GM_1M_3}{|\vec{P}_1-\vec{P}_3|^3}\left( \vec{P}_1-\vec{P}_3\right)\\M_2 \ddot{\vec{P_2}} = -\frac{GM_2M_1}{|\vec{P}_2-\vec{P}_1|^3}\left( \vec{P}_2-\vec{P}_1\right) -\frac{GM_2M_3}{|\vec{P}_2-\vec{P}_3|^3}\left( \vec{P}_2-\vec{P}_3\right)\\M_3 \ddot{\vec{P_3}} = -\frac{GM_3M_1}{|\vec{P}_3-\vec{P}_1|^3}\left( \vec{P}_3-\vec{P}_1\right) -\frac{GM_3M_2}{|\vec{P}_3-\vec{P}_2|^3}\left( \vec{P}_3-\vec{P}_2\right)\end{array}

It could be worse; it could be that somehow the other bodies interact with each other in such a way that the total force is different than just the sum of their independent forces.  In fact, almost any other set up is worse.  Even things like declaring “only the closest body attracts”.  That would be much worse.

So, even if you set up one of the bodies to be stationary (like in the solution to the 2-body problem), you still end up with N-1 bodies flying about, and you still have \frac{N(N-1)}{2} force terms to worry about (N-1 for N equations, but by Newton’s third law the force of A on B is equal to the force of B on A, so divide by 2).

Exact solutions just don’t seem to exist.

Posted in -- By the Physicist, Astronomy, Equations, Philosophical, Physics | 29 Comments

Q: How are fractals made?

Posted on September 29, 2011 by The Physicist

Physicist: There are a lot of ways.

A fractal is just a structure that stays interesting no matter how far you zoom in.  More than that, generally you can’t tell how far you’ve zoomed in (it looks the same at many different size scales).  Making up new fractals is surprisingly easy.

The most famous one (that you’ll find on posters in dorm rooms) is the “Mandelbrot set”, followed by the “Sierpinski Triangle”.  I haven’t taken a survey, but these seem to be the most popular.

Sierpinski Triangle.

It’s pretty straightforward how the Sierpinski triangle is made: make a triangle, put three triangles in its corners, put three triangles in those triangle’s corners, etc.  This sort of idea: take a shape and then populate it with smaller versions of itself, is arguably the most common way to generate fractals.

The Mandelbrot set on the other hand involves complex numbers and computing power that wasn’t available until the ’80s.

The Mandelbrot set is the black region. When you zoom in on the edge of the black area you'll find that the same patterns show up over and over no matter how far you zoom in.

To determine if a point is in the Mandelbrot set, start with the recursion:

zn+1 = zn2 + c

z0 =0

This means “square what you’ve got, add c, then take the result, square it, add c, then take the result, …”

For different values of c the string of numbers you get out does different things.  For example;

for c = 1, you get: 0, 1, 2, 5, 26, 677, … (that’s 0, 1=02+1, 2=12+1, 5=22+1, …)

for c = -0.5, you get: 0, -0.5, -0.25, -0.4375, -0.30859375, -0.404769897, …

The Mandelbrot set is defined as the set of values of c that lead to strings of numbers that stay bounded.  So, c=-0.5 is in the set because the string of numbers it makes stays in more or less the same place (it stays between -0.5 and 0 forever).  But c=1 is not in the set because its string of numbers blows up.

It’s a little more complicated because you actually consider complex numbers (which is why the picture you get is in a plane).

Where the Mandelbrot set sits. As you might expect, -0.5 is in the set and 1 is not.

Finally, the set itself isn’t terribly interesting, but its boundary is.  The boundary between what’s in the set and what’s not (what generates a string of numbers that behaves, as opposed to a string that blows up) is infinitely squiggly.

Almost every time you see the Mandelbrot set, colors are included that indicate how fast the strings generated by numbers not in the set blow up.  Also, without colors it’s boring.

Another classic is the Dragon Curve:

The Dragon Curve (some of it at least).

The Dragon Curve is what you get what you fold a piece of paper in the same direction over and over (forever), and then unfold it at 90° angles.

"Unfolding paper" to create the Dragon Curve

Long story short: there are many ways to create fractal patterns, but it’s not always easy to guess what technique will lead to a fractal until you try it.

Posted in -- By the Physicist, Geometry, Math | 9 Comments

Q: CERN’s faster than light neutrino thing: WTF?

Posted on September 23, 2011 by The Physicist

Physicist: The story here is that CERN has been generating neutrinos, firing them 730km, to a detector in Gran Sasso, Italy, and those neutrinos have been consistently (so far as their instruments say) arriving 60 ns (0.00000006 seconds) earlier than they should.

These sorts of things crop up every few months, with varying credibility, but the credibility of this group is higher than most.  Faster than light claims have always (so far…) turned out to be a hoax, or a misunderstanding, or an error.

In this case it’s very likely to be an error.  When you’re talking about neutrinos you’re usually talking about just a couple of data points.  You generate a fantastic number in beam-form somewhere, fire it many times through the Earth at a detector far away and, with luck, you’ll detect one.

There are a lot of ways for a 60 nanosecond or 60 foot (light speed is about 1 foot per nanosecond) error to creep into an experiment involving a beam of “ghost particles” traveling 730km, from CERN to Gran Sasso, that produces no more than one or two data points at a time.

The neutrino beam generated at CERN is passed through the Earth and detected in Italy. Neutrinos are hard to detect because they barely interact with matter at all. Hence the whole “don’t worry about the Earth being in the way” thing.

This is news firstly, I suspect, because everybody hates the light-speed cap.  Ever since 1905, when Einstein did his big, fancy “you can’t go faster than light” paper, there has been an unending tide of people coming up with ideas for moving faster than light.  Every single one has utterly failed, but the point is that the cap has a way of getting under everyone’s skin.

Human nature: If you tell someone they can’t travel faster than light, then suddenly that’s all they’ve ever wanted to do.

But mostly this is news because special relativity (which immediately implies the light speed cap) has been verified thousands and thousands of times in the last hundred and six years.

If you were to hear “scientists find that mustachioed men tend to ride unicycles more often than their clean-shaven brethren” you wouldn’t think twice about it (well, maybe twice), because there isn’t a towering monolith of evidence to the contrary.  You might wonder why they bothered looking into it, but whatever.

At the other end of the spectrum is relativity, which is really what’s at stake.  It is so well tested, and so well verified, that it has become the yardstick against which other physical theories are measured.  Often you can hear physicists laughing (cackling) at other physicists and saying things like “… and their scalar field wasn’t even Lorentz invariant!” (translation: “their thing violates relativity”).  Every single time anyone has ever made the claim that they have evidence that there’s something wrong with relativity, they’ve turned out to be wrong.

Unlike the sound barrier or the 4-minute mile, which were thought to be impossible merely because they were very difficult, the speed of light is inexorably tied up in the nature of existence, and matter, and time, and all that falderal.

So the reaction of most physicists to the CERN faster-than-light fiasco is: “wow… they really messed something up”.  In fact, the physicists at CERN (being physicists themselves) published the results not so much to say “hey, look what we did” so much as “fellow dudes and dudets… we really messed something up”.

If it’s a real discovery we should be extremely interested!  But, don’t hold your breath.

Update: They did indeed mess something up.

Posted in -- By the Physicist, Experiments, Paranoia, Relativity, Skepticism | 32 Comments