The original question was: I can’t find a consistent answer to this question; please help. A spaceship leaves Earth and heads to a star 4 light years away at 80% of light speed. An observer on Earth knows that the spaceship’s clock will run slower than his clock by 40% for the entirety of the journey (according to the Lorentz formula).
According to the Earth-based observer, the spaceship will arrive at the star in 5 years. However, because of time dilation, the spaceship’s clock will only read 3 years of elapsed time on arrival. To an astronaut on the spaceship, the distance to the star appears to be just 2.4 light years because it took him just 3 years to get there while traveling at 80% light speed.
This situation is sometimes explained as a consequence of length contraction. But what is it that’s contracting? Some authors put it down to space itself contracting, or just distance contracting (which it seems to me amounts to the same thing) and others say that’s nonsense because you could posit two spaceships heading in the same direction momentarily side by side and traveling at different speeds, so how can there be two different distances?
So what is the correct way to understand the situation from the astronaut’s perspective?
Physicist: Space and time don’t react to how you move around. They don’t contract or slow down just because you move fast relative to someone somewhere. What changes is how you perceive space and time.

There’s no true “forward” direction and, terrifyingly, there’s no true “future” direction or even “space but not time” direction. All of these directions and the lengths of things in those directions are subjective and even, dare I say, relative.
When you measure the length of something in space (in other words, “normally”), the total length isn’t just the length in the x or y directions, it’s a particular combination of both that works out exactly the way you’d think it should. When you measure the length of something in spacetime, the total length isn’t just the length in the space or time directions, it’s a particular combination of both that works out in more or less the opposite of how you’d think it should.
We don’t talk about the three dimensions of space individually, because they’re not really distinct. The forward, right, and up directions are a good way to describe the three different dimensions of space, but of course they vary from perspective to perspective. Just call someone from the opposite side of the planet and ask them “What’s up?” and you’ll find yourself instantly embroiled in irreconcilable conflict. Everyone can agree that it’s easy to pick three mutually perpendicular directions in our three-dimensional universe (try it), but there’s no sense in trying to specify which specific three are the “true” directions.
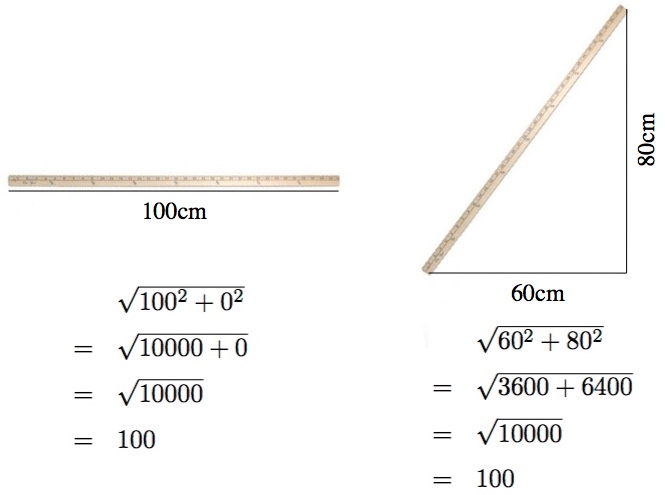
If you insist on measuring things in only one direction, then different perspectives will result in different lengths. To find the total length, d, requires doing a couple measurements, x and y (and z too, in 3 dimensions), and applying some Pythagoras, d2=x2+y2.
A meter stick is a meter long (hence the name), so if you place it flat on a table and measure its horizontal length (with a… tape measure or something), you’ll find that its horizontal length is 100cm and its vertical length is zero. Given that, you could reasonably divine that it must be 100cm long. But if you tilt it up (or equivalently, tilt your head a bit), then the horizontal and vertical lengths change. There’s nothing profound happening. To handle a universe cruel enough to allow such differing perspectives we use the “Euclidean metric”, 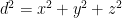 , to find the total length of things given their lengths in each of the various directions. The length in any given direction (x, y, z) can change, but the total length (d) stays the same.
, to find the total length of things given their lengths in each of the various directions. The length in any given direction (x, y, z) can change, but the total length (d) stays the same.
Einstein’s big contribution (or one of them at least) was “combining” time and space under the umbrella of “spacetime”, so named because Germans love sticking words together in a traditional process called (roughly translated) stickingwordstogethertomakeonereallylongdifficulttoreadandoftunpronounceableword.
The different spatial dimensions are equivalent. To see for yourself, walk north and south, then walk east and west. Unless you’re carrying a compass, you shouldn’t notice any difference. But clearly time is different. To see for yourself, first walk north and south, then walk to tomorrow and back to yesterday. So when someone cleverly volunteers “we live in a 4 dimensional universe!”, they’re being a little imprecise. Physicists, who love precision slightly more than being understood, prefer to say “we live in a 3+1 dimensional universe!” to make clear that there are three space dimensions and one time dimension.
But while time and space are different, they’re not completely separate. In very much the same way that the forward direction varies between perspectives, the “future direction” also varies. And in the same way that rotating perspectives exchanges directions, moving at different velocities exchanges the time direction and direction of movement. The total “distance” between points in spacetime is called the “interval”, L. For folk familiar with the Euclidean metric, the “Minkowski metric” should look eerily familiar:  . Some folk will flip the sign on this,
. Some folk will flip the sign on this, 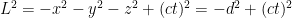 , because it makes it a little easier to talk about the time experienced on a particular path (in fact, I’m gonna do that in a minute), but the important thing is not the sign of this equation, it’s that it’s constant between different perspectives. It should bother you that
, because it makes it a little easier to talk about the time experienced on a particular path (in fact, I’m gonna do that in a minute), but the important thing is not the sign of this equation, it’s that it’s constant between different perspectives. It should bother you that  can be negative, but… don’t worry about it. It’s fine.
can be negative, but… don’t worry about it. It’s fine.
If you’re wondering, the spacetime interval is a direct consequence of rule #1 in relativity: the speed of light is the same to everyone. The short way to see this is to notice that if you find the interval between the start and end points of a light beam’s journey, the interval is always zero because 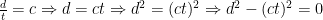 . The long way to see why the interval is what it is, is a little long.
. The long way to see why the interval is what it is, is a little long.
There are two things to notice about the spacetime interval. First, that “c” is the speed of light and it basically provides a unit conversion between meters and seconds (or furlongs and fortnights, or whatever units you prefer for distance and time). So 1 second has an interval of about 300,000 km (one “light-second“), which is most of the distance between here and the Moon. It turns out that the speed at which light travels comes from the “c” in this equation. So the speed of light is dictated by the nature of space and time (as described by the Minkowski metric), not the other way around. Which is good to know.
Second and more important is that negative. That really screws things up. It is arguably responsible for damn-near all of the weird, unintuitive stuff that falls out of special relativity: time dilations, length contractions, twin paradoxes, Einstein’s haircut and marriages, everything. In particular (and this is why the exchange between distance and duration is so unintuitive), if  is constant, then when d increases, so does t.
is constant, then when d increases, so does t.
This is in stark contrast to regular distance, where if 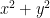 is constant, an increase in x means a decrease in y. Picture that in your head and it makes sense. Picture relativity in your head and it doesn’t.
is constant, an increase in x means a decrease in y. Picture that in your head and it makes sense. Picture relativity in your head and it doesn’t.
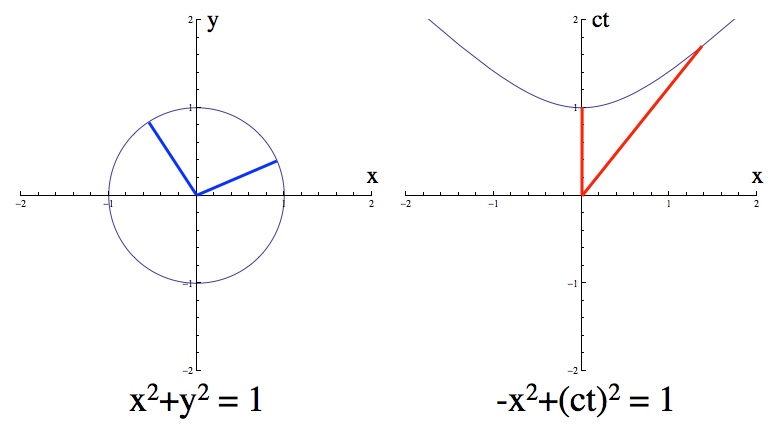
Left: The points a distance of 1 away form the origin form a circle. The two blue lines are the same length. Right: The points a spacetime interval of 1 away from the origin form a hyperbola. The two red lines are the same “length”. Here time is the vertical axis and one of the space directions is the horizontal axis. So if you sit still you’d trace out a path like the first red line and if you were moving to the right you’d trace out a path like the second red line.
Now brace yourself, because here comes the point. The original question was about a journey that, from the perspective of Earth, was d = 4 light-years long, at a speed of v = 0.8c, and taking t = 5 years. The beauty of using “light units” (light-years, light-seconds, etc.) is that the spacetime interval is really easy to work with. The interval between the launch and landing of the spaceship is:
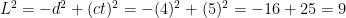
So the interval is L = 3 light-years.
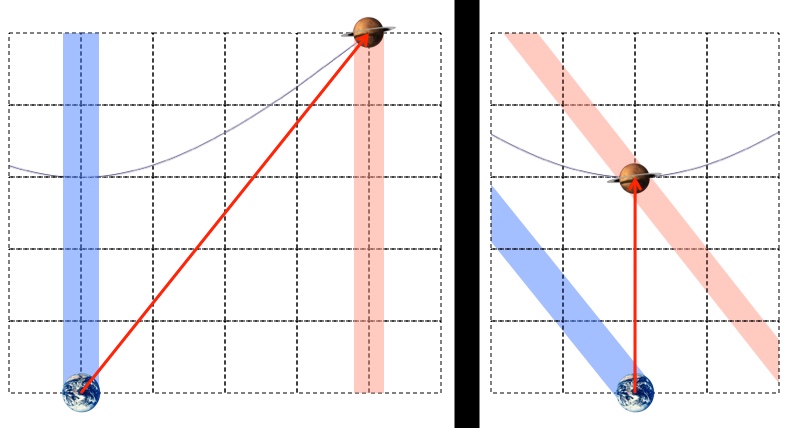
Left: Earth and an alien world sit still (travel through time but not space) 4 light-years apart while a spaceship traveling to the right at v=0.8c takes 5 years to travel between them. Right: A spaceship sits still (travels through time but not space) for 3 years while Earth and an alien world travel to the left at v=0.8c.
Like regular distance, the power of the spacetime interval is that it is the same from all perspectives. From the perspective of the spaceship the launch and landing happen in the same place. It’s like a narcissist on a train: they get on and get off in the same place, while the world moves around them. So d = 0 and it’s just a question of how much time passes:

So, t = 3 years because 3 light-years divided by the speed of light is 3 years.
So just like changing your perspective by tilting your head changes the horizontal and vertical lengths of stuff (while leaving the total length the same), changing your perspective by moving at a different speed changes length-in-the-direction-of-motion and duration (while keeping the spacetime interval the same).
That’s time dilation (5 years for Earth, but 3 years for the spaceship). Length contraction is a little more subtle. Normally when you measure something you get out your meter stick (or yard stick, depending on where you live), put it next to the thing in question and boom: measured. But how do you measure the length of stuff when you’re moving past it? With a stopwatch.

How can you tell that mile markers are a mile apart? Because when you’re driving at 60 mph you see one a minute.
So, like the original question pointed out, if it takes you 3 years to get to your destination, which is approaching you at 0.8c, then it must be 3×0.8 = 2.4 light-years away. Notice that in the diagram with the planets above, on the left they’re 5 light-years apart and on the right they’re 2.4ish light-years apart (measure horizontally in the space direction).
It feels like length contraction should be more complicated than this, but it’s really not. You can get yourself tied in knots thinking about this too hard. After all, when you talk about “the distance to that whatever-it-is” you’re talking about a straight line in spacetime between “here right now” and “over there right now”, but “now” is a little slippery when the “future direction” is relative. Luckily, “time multiplied by speed is distance” works fine.
There are a few ways to look at the situation, but they all boil down to the same big idea: perspectives moving relative to each other see all kinds of things differently. Reality itself, space and time and the stuff in it doesn’t change, but how we view it and interact with it doesn’t quite follow the rules we imagine.
. By looking at 3 (or any other number you like) multiplied by smaller and smaller integers you see a pattern:
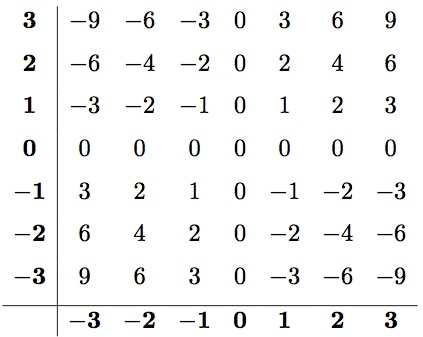
“), then the rows and columns that go through it will suddenly have to switch patterns (e.g., “increasing by 3’s” to “decreasing by 3’s”) when they pass zero. In some sense, the rules for signs are set up so that multiplication tables like this follow a nice, simple pattern.
,
, and
” is a clean, reasonable way to define multiplication. But does it work with the rules of arithmetic?
, is one of the backbone rules upon which all of arithmetic is built. In fact, this property is literally the thing that defines the relationship between addition and multiplication! For example,
rule”. For example,
and
.
“, then you’ll find the distributive property doesn’t work. For example,
and
. The discerning eye will note that 5≠25, so
. In other words, we need to use “
” in order for arithmetic to work.
” rule, but refuse to accept the “
” rule, then consider this:
and
.
” rule is kinda hard to avoid. Using a different rule means asking a lot of hard questions, like: What is negativeness? Which rules of arithmetic are worth keeping? What is the sound of negative two hands unclapping?