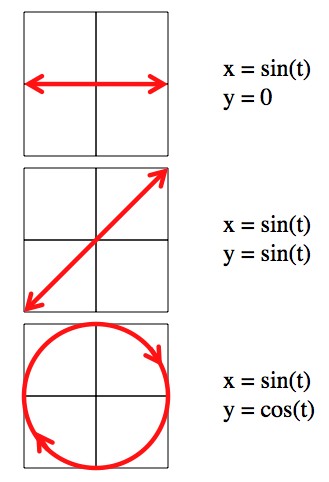Q: Would it be possible for humans to terraform mars?

Posted on July 27, 2011 by The Physicist

Physicist: In terms of feasibility: no.  In terms of being remotely possible: yes, but probably not permanently.

Mars is much colder than Earth, has no water, and effectively no air.  On the up side, unlike many planets, you can stand on Mars (it’s solid), and its day is nearly the same as Earth’s (24 hours, 40 minutes).  Despite the bad news that follows, Mars is the best candidate for terraforming (making more Earth-like).

First problem: Mars is cold.  The most searing heat wave on Mars would barely melt water.  Unfortunately, this is a problem with Mars’ distance from the Sun.  The only way to get Mars warm would be to create an intense greenhouse effect by mixing up the right atmosphere.

The size of the Sun as seen from Earth (left) compared to the size of the Sun as seen from Mars (right). There's not much sunlight, and not much that can be done about it.

So we need to add an atmosphere, which is pretty hard to come by.  Mars has a little under 1% of the atmosphere we enjoy on Earth, so we’d be practically starting from scratch.

Our atmosphere is 99% nitrogen and oxygen. The last 1% is almost all argon. Carbon dioxide makes up a paltry 0.04% of our air. Moral is: we have a big, complicated atmosphere.

Mars did, at one time, have an atmosphere.  The best theory today is that when Mars lost its magnetic field the Solar wind, that would otherwise be deflected, was free to gradually strip away Mars’ air.  Mars also has about 1/3 of Earth’s gravity, making the process substantially easier.

So there’s some possibility that even if we did manage to establish a dense, warm atmosphere that it would suffer the same fate as the first atmosphere (after several thousand years).  Every couple of millennia it may be necessary to touch-up the atmosphere.

The amount of green house gasses you’d need to keep the surface water liquid is very likely to be toxic.  It’s been shown that human beings can survive CO2 concentrations as high as 4% (the research so far hasn’t killed anybody, but it has made some people sick).  Unfortunately, concentrations higher than 4% are likely to be necessary to maintain a liquid water environment, and even 1% isn’t particularly healthy.

The atmosphere of Mars at the same scale as the picture above. If you were to stand on Mars without a space suit you would get a spectacular full-body hickey. In fact, the low (almost zero) pressure is probably the first thing that would kill you, so wear a space suit if you're going to Mars.

Other gases can be substituted for CO2 to create a green house effect.  But most have other problems: too much methane could make the atmosphere explosive, and nitrous oxide tends to make people… weird.  The best candidate is probably sulfur-hexafluoride (SF6), which is more than 20,000 times more effective than CO2 as a greenhouse gas, and is non-toxic.  There are, however, more subtle drawbacks to SF6 and it would be pretty difficult to synthesize enough.

As the Sun gets brighter, we should find that in a couple billion years Mars will be in the “goldilocks zone” (and Earth won’t) and that whole “toxic concentrations of green house gas” problem becomes moot.  It’ll be naturally warm enough in Mars’ orbit for liquid water.

It would also be nice to have oceans on Mars.  Oceans are really good at circulating heat, “smoothing out” temperature fluctuations, and generally give rise to climatological niceness.  Our oceans can store and release just a hell of a lot more heat than our atmosphere.  In order to create oceans on 2/3 of Mars’ surface with a depth of 3 to 4 km (like our oceans) would require about 350 million cubic km of water.  Luckily, we’ve got big blobs of water (or ice at least) flying around the solar system in the form of comets.  But to top off Mars’ oceans would take somewhere around 3 to 4 million comets.  To date there are only around 6,000 known comets, but there are likely to be billions or trillions more out past Pluto’s orbit.  I wonder if Halley’s comet would be protected as a historical landmark?

Comets are convenient because the water they carry doesn’t have to be hauled off of another planet’s surface (which costs a lot of energy).  Instead you can “nudge” them into orbits which intersect Mars.  It’s worth noting: you wouldn’t want to be anywhere on the surface when the oceans are being set up.

The oceans of Mars: step 1.

Water is a great material because it’s mostly oxygen, which is the most important part of the atmosphere (in my very humble opinion).  You could turn some of the new Martian seas into the bulk of the new atmosphere with gigantic electrolysis plants, which would use electricity to break down the water (H2O) into hydrogen and oxygen.

If the goal is just to have life on Mars, as opposed to human life, then we may already be able to engineer something that could scratch out a living on Mars.  Bacterial extremophiles, maybe water bears, that sort of thing.  There’s a decent chance that there are patches of damp dirt deep below the Martian surface that could support some forms of bacteria.

The Mars impact picture was painted by Don Dixon.

Posted in -- By the Physicist, Astronomy, Biology, Physics | 31 Comments

Q: Can light be used to transfer energy instead of power lines?

Posted on July 22, 2011 by The Physicist

The original question was: Is it possible that, when more efficient methods of harnessing light energy are established, light could be used as a means to transfer massive amounts of energy (for instance, enough to power a city) without physical wires? What are some of the obstacles that would prevent such energy transfer?

Physicist: It depends on how liberal your definition of “light” is.

Way back in the day Tesla did a whole bunch of research into exactly what you’re talking about: wireless transmission of power.  One application he envisioned (and this is one of the draw backs) was an honest-to-god death ray.

Nikola Tesla set the bar pretty high for every mad scientists that followed. Here he's showing off one of his more terrifying inventions: the desk chair.

Didn’t work.  Not even close.  Ironically, Tesla’s grandiose claims and electrically-based publicity stunts have made him a magnet for “alternative science“.

There is some active research in using microwaves and magnetic coils to transfer energy, but so far the results have been pretty underwhelming.  Technically, all transformers are wireless.  They use a coil to generate a changing magnetic field, and that changing magnetic field carries the energy to another coil that turns it back into electricity (at a different voltage).

Transformers (the can) are used to "step down" voltage from power lines so that the electricity in our homes doesn't kill the hell out of us. In the process, it efficiently and wirelessly transfers energy over distances as large as several millimeters. The energy takes the form of magnetic waves, which is technically light (technically).

What you’d really like is a beam of energy.  Low frequency waves tend to spread out a lot (which is part of why transformers are so compact), and higher frequency waves (microwaves and radar, that sort of thing) tend to interact with matter other than the specially constructed receivers (i.e., frying stuff in the beam).

You also have to be extremely careful about how the receiver is built.  For example, when you point a telescope at the sun you have to be very sure that the lenses are clean.  A tiny bit of grit can absorb light, heat up, blacken the lens, making it absorb light, making it heat up and blacken more…

Similar things (melting) happen with high-energy, high-frequency receivers, which is profoundly unfortunate, since without high-frequencies it’s basically impossible to aim your beam.

A laser capable of powering Los Angeles (about 6 gigawatts) can melt a school bus in a little under one second (make a note, that was the least useful statistic you’ll read this month).  So, you need to make sure that whatever system you have for catching the beam had better be really efficient.  Even at 99% efficiency you’d need a huge cooling system (enough to keep a bus from melting in about a minute).  The whole set up is just an accident waiting to happen.

Start walking home kids. This bus is for science.

For comparison, the most efficient solar panels today can convert about 50% of the light that falls on them into electricity.  You could use many beams to spread out the heating, but ultimately wires are a pretty good way to go.

On the other hand, a beam would be the easiest way to transfer energy between the ground and space (not that it easy even then).

Posted in -- By the Physicist, Engineering, Physics | 7 Comments

Particle physics, neutrinos, and chirality too!

Posted on July 17, 2011 by The Physicist

Physicist: This was an email correspondence that was too interesting to abandon, but covered so much ground that it didn’t easily parse into just a couple of questions.

Q: What force is the ‘kinetic’ force? If 2 particles bounce of each other (can particles do that anyway?), what force carrier is exchanged to change the momentum of the particles?

 

A: All the force carriers carry momentum.  Particles on their own don’t bump into each other, they need some kind of “mediating particle” to do the bumping for them.

 

Q: What is the current accepted notion of proton decay?

 

A: From what I gather, the decay of protons is possible in theory, but (according to theory) so unlikely during any reasonable time span that we’ll never see it.

 

Q: What is the chance of 4th generation particles existing (Leptons other than electrons, muons, and tauons)?

 

A: Maybe?  They would need to have amazingly high mass to have eluded detection so far (more on that below).

 

Q: What is chirality and helicity? And (I believe related): What is polarization and spin?

 

A: Chirality is essentially the “handedness” of a thing.  Cork screws and DNA are great examples.  You’ll notice that when you try to get a corkscrew into a cork you have to turn it in a particular direction, but if you were to turn it around (push it into a cork backward) you still turn it the same way (it helps to be holding a corkscrew for this to make sense).

If you imagine tracing the path of the corkscrews on the left with your finger, you'll notice that there's no difference between them. They always turn in the same direction, regardless of orientation. But, if you reflect the corkscrew (right), then the direction of the twist reverses. Things that switch when reflected have "chirality".

The corkscrew has a definite direction it needs to turn, regardless of its orientation.  It has a particular “chirality” (or in this case “helicity”).  If you look at the reflection of that same corkscrew in a mirror you’ll notice that it has the opposite chirality.  To prove it, try opening a bottle of wine while looking in the mirror.  Although it sounds a little like a “silence of the lambs” thing to do, you’ll notice that while your corkscrew turns one way, the reflection turns the other way.

Jame "Buffalo Bill" Gumb investigates chirality, and probably nothing else.

The chirality you hear about in particle physics and quantum field theory is usually in reference to something a bit more subtle and less interesting than corkscrews and spinning things (which are usually described as having helicity), and you have to get shoulder-deep in the math before you can reach it.  Saying “according to field theory, all particles have the same chirality”, means about as much as “every gloopb is also a brotunm”.  Without extensive mathematical study, it isn’t saying much.

As for polarization: light is a “transverse wave“, which means it waves back and forth in a direction perpendicular to the direction it’s traveling, like a wave on a rope, instead of waving back and forth in the direction it’s moving, like sound and pressure waves.

But (in 3 dimensions) there are two directions that are perpendicular to the direction of motion.  For example, if a photon is coming straight at you, the wave could be either horizontal or vertical.  These options are the “linear polarizations” of the light.  It can be in either polarization or (because of the weirdness of quantum mechanics) a combination of both, which includes things like diagonal polarization.

You can also describe the polarization in terms of “circular polarization”, in which one polarization “corkscrews” clockwise as the photon travels, and the other corkscrews counter-clockwise.  You can describe each circular polarization in terms of a weird combination of the linear polarizations, and vice versa.

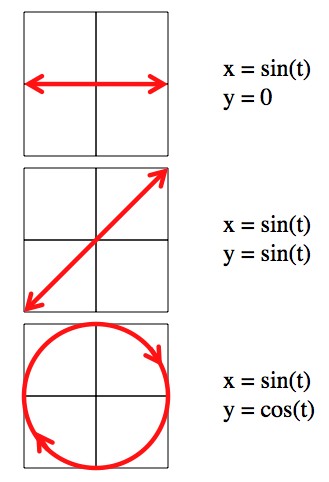
You can describe the linear polarizations in terms of waves (Sines and Cosines) in the x and y directions. By delaying one wave with respect to the other (which is really the only difference between sin and cos) you can get elliptical or circular polarizations.

This is one of those beautiful examples of the universe being horribly obtuse.  You’d expect that, “in reality”, light is either linearly or circularly polarized.  But all of the relevant laws can be written either way, and in physics: if it makes no difference, there may as well be no difference.

“Spin” is also sometimes called “intrinsic spin”.  It is essentially the angular momentum of a particle.  However, particles generally have more angular momentum that should be possible.  For example, electrons have “1/2 spin”, which is a certain amount of angular momentum (specifically: 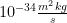10^{-34} \frac{m^2 kg}{s}).  But, since they’re so small, they need to be rotating very quickly to have that much angular momentum.  If you do the math you find that electrons, for example, need to be rotating much faster than light (which is impossible).  So, spin is a property of particles that carries angular momentum, but doesn’t actually involve rotation.  It’s weird stuff.

For fairly obscure reasons spin can only takes values that are multiples of ½ (0, ½, 1, 3/2, …).  What’s entirely cool, is that those fairly obscure reasons are based on the fact that we live in a 3-dimensional space.  In two dimensions you can have particles with any spin.  Particle physics, who aren’t nearly as funny as they’d have you believe, call them “anyons” (for “any spin”).

 

Q: So chirality is just a property some particles have for a really complicated math-y reason. Fair enough. Does that have some interesting implications?

 

A: With a fairly liberal definition of interesting: kinda.  All particles in our universe have the same chirality, but that isn’t quite coincidental.  It’s more “fun fact” than useful.

 

Q: What is the difference between neutrino’s and anti-neutrino’s?  There was a period where they thought that all neutrino’s were massless.  In that time, how could they differentiate the electron, muon and tauon neutrino?  Do the heavier neutrino’s generally move slower or do they have more energy which results in roughly the same speed?

Quick aside: Electrons are members of a particle family called “Leptons”.  The leptons include electrons (lightest and stable), muons, and tauons (both are far heavier, and unstable).  In addition, all three have an associated “neutrino”, and all six of them (the electrons, muons, tauons, and each of their neutrinos) have an anti-particle twin.  That’s 12 particles total.  Neutrinos are very difficult to study because they just barely interact with ordinary matter.


A: They always seem to travel at light speed, or more likely: really close to light speed.  They’re light-weight enough that a tiny bump really sends them flying.  It turns out that the different neutrinos are all different states of what is essentially the same particle (kinda like how the different polarizations of a photon are different states of the same particle).  As a neutrino propagates through space it actually changes from one type to the other to the other and back.  At least, as time goes on the chance of the neutrino being discovered to be either electron, muon, or tauon changes.  This is (in a handwavy way) due to each state having a different frequency, which in turn is due to the different states having different masses.  The difference between neutrinos and anti-neutrinos is exactly the difference between matter and anti-matter.

You differentiate between them during the (extremely rare) interaction events.  To conserve “lepton flavor” an interaction that destroys a muon neutrino must create a muon, and one that destroys an anti-electron-neutrino must generate an anti-electron, and so on.  Basically, you suddenly see the appropriate particle produced or destroyed.

 

Q: But, when they first discovered neutrino’s and didn’t know there were different types how could they still expect different types being produced?  Especially since they didn’t have any differing characteristics between the different neutrino’s.  So how did they just ‘know’ that the particle created when a muon or tauon decayed wasn’t an electron-neutrino?

 

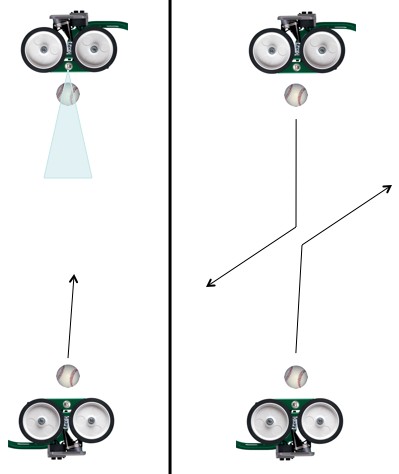
A: When new particles are produced they’re flung off with random directions and momenta, contingent on the total momentum of the system being conserved (so not completely random).  During neutron decay (also called beta decay) we see the resulting proton and electron flying off in such a way that it was very likely that there was only one new particle being produced (now known to be the anti-electron-neutrino).  But during muon decay we see the resulting electron flying off in a manner consistent with the rapid production of two particles (anti-electron and anti-muon neutrinos).  In the picture below the \overline{\textrm{overbar}} means “anti-“.

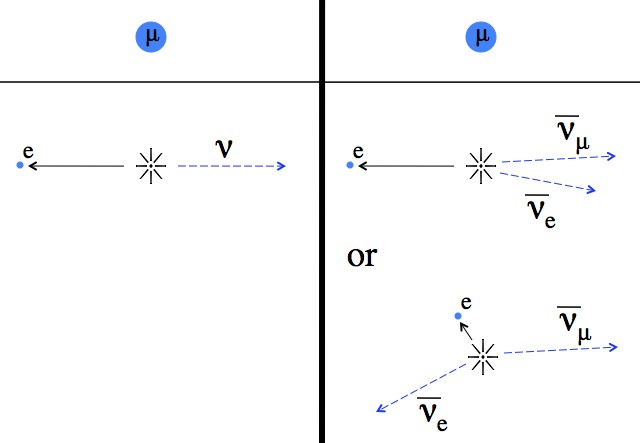
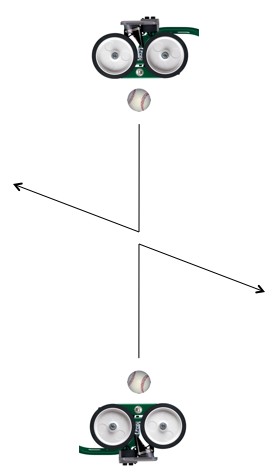
Muon decay: a stationary muon suddenly decays into an electron and neutrinos. Left: if hypothetically, during muon decay, only one neutrino were created then since the total energy released is always the same and momentum always needs to be balanced, the electron (the only thing we see) would always be ejected at the same speed. Right: in practice we see the newly created electron ejected at a wide variety of speeds. It takes a bit of analysis, but what we see is consistent with the creation of two unseen particles.

More than that, the extremely long lifetime of the muon (about a microsecond) implied the existence of an unknown conserved quantity (lepton flavor).  “Conserved quantities” force particles to maintain a variety of balances and to “carefully consider everything” before decaying.  Basically, more things have to fall into place for a decay to happen.  That increases the half-life.

More than that, after extensive calculations the total neutrino generation rate of the Sun’s core was (accurately) estimated, but when we started measuring the solar neutrinos we found that we were only finding about one third of what we should have (the neutrinos evolve from one form to another, and by the time we see them they’re thoroughly scrambled up).  This (among other similar experiments) is good evidence that we won’t find a fourth lepton.

Using nothing more than: neutrinos, an array of gigantic detectors filled with the purest water in the known universe, and more computing power than most countries, this image of the neutrino-producing core of the Sun was created.

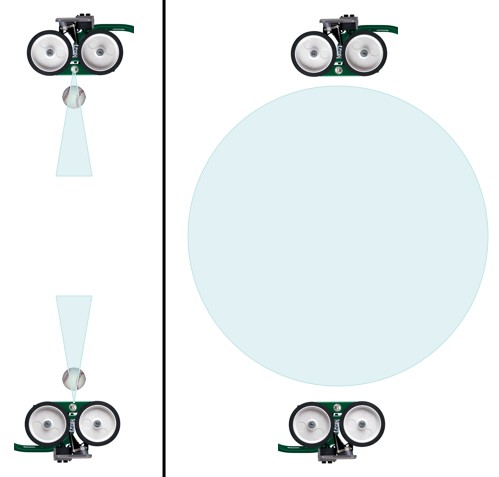
A similar, more controlled, experiment involves creating the neutrinos ourselves.  Accelerate protons up to huge energies and then slam them into a brick of something solid (steel or tungsten or something).  That sudden splash of energy tends to generate pions (“pie ons”) that in turn tend to immediately decay into muons and muon-neutrinos (both “anti” and “normal”).

Muon-neutrino generator (particle accelerator not shown).

Neutrinos, being basically ghost particles, pass right out of the lab no problem, while every other kind of particle is left behind.  You can then set up another lab miles away (and generally deep underground) to detect the neutrinos produced (for example, the Super-K).  These detectors are essentially huge water tanks surrounded by very, very sensitive cameras.

Electron-neutrinos (for example) can be absorbed by neutrons to induce beta decay.  This is rare (60 light years of lead can block about 50% of a neutrino beam), but if you’ve got an accelerator pumping out neutrinos, then you can catch a few.

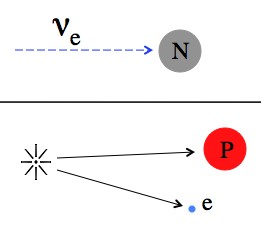
"Induced beta decay". An electron-neutrino can cause a neutron to turn into a proton and an electron. A muon neutrino would create a proton and a muon. The anti-neutrinos can induce a reverse-beta-decay, where a proton is turned into a neutron and anti-electron (or anti-muon or anti-tauon).

Since the neutrinos were produced from an extremely high energy reaction they carry quite a punch.  The particles resulting from the interaction move fast enough through the water in the detector that they form “Cherenkov radiation”, which is essentially a “sonic boom made of light” (or, the result of it at least).  By looking at how the “boom” hits the light sensors around the detector you can get energy and direction information about the original particle.

 

Q: Are force-carrying particles launched in random directions at random times or have they got a higher change to be produced if another particle they can react with is close?  If they are randomly produced, it would mean that there is a chance that, for instance, a gluon could travel really far before reaching something to react with, right?

 

A: The force carrying particles are almost always “virtual particles“.  Statements about when they’re emitted, and where they are, and why they’re emitted, are all a little senseless.  Virtual particle interactions necessarily involve super-positions of many states of the particles, including states where the particles don’t exist at all.
The force carries can’t do anything to a particle unless there’s another particle around to do the opposite (i.e., the virtual photons produced by an electron can’t push it around unless there’s another charged particle that can move in the opposite direction and conserve momentum).  Unfortunately, this is another example (like the double slit, or entanglement, or whatever) of how quantum mechanics stomps all over causality.  Does the force carrier just happen to push the other particle because it got in the way, or was the force carrier only present because there was another particle to be pushed?  The answer to both questions is; yes…ish.

 

Q:  Why can’t quarks exist separately, but only in pairs/triplets. Why don’t gluons travel very far? Why is it that gluons can keep quarks inside of protons and neutrons and they can also keep protons and neutrons together in a nuclear core?

 

A: The short, annoying answer that I usually hear, is that the energy required to separate quarks is enough to create enough new quarks that none of them are left alone.  The more technical answer is the quark interactions have to preserve “color”.  In physics we’ve got all kinds of conserved quantities: energy, momentum, baryon number, lepton flavor, color, etc.  In any arrangement of quarks the “color” has to be zero.  As in “red and anti-red” or “red, blue, and green”.  Overall, the net color has to cancel.  Of course, that’s not an explanation so much as a statement of fact.  But as for why?  Who knows.  It’s just another conserved quantity.

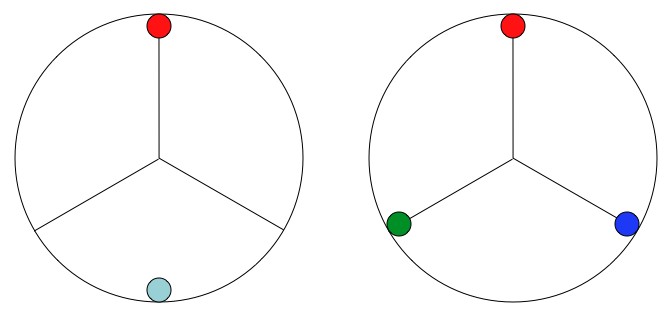
Every particle has neutral "color", by "balancing the color wheel". There isn't any actual color going on, it's more a useful mnemonic for keeping track of things.

Gluons are extremely massive particles.  In order to be created (generally) the energy required is much higher than the energy present, which means that in order to exist the gluons have to “borrow against the uncertainty principle”.  However, having an energy uncertainty that high means having a time uncertainty that’s small.  Small enough, in fact, that these gluons don’t have time to cross a nucleus before they blink out again.

 

Q: What is group theory and why is it related to quantum physics so much?

 

A: Group theory is an extremely generalized way of talking about sets of things, and the behaviors of those things.  For example, the orientation of a particle is a set (of all the different ways it can be aligned), and all the ways you can rotate it are the “group actions” on the set of orientations.  The age of intuitive physics ended at the beginning of the 20th century (relativity and quantum mech), and since we can’t use intuition to predict the behaviors of quantum mechanical things, we use group theory.
Group theory can be used in traditional physics, it’s just that it’s a little complicated, and unnecessary (the behavior of traditional physics is fairly intuitive).  In quantum mech, there really aren’t options.  For example, if you rotate a chair (or anything else) through 360° it returns to where it started.  You can describe that using group theory, but needn’t bother.  I mean, it’s a chair, how much math do you need?  An electron, on the other hand, has to rotate through 720° to return to its original position.  That’s really impossible to talk about normally (sober), so group theory is what you’re left to work with.

 

Q: And finally: Feynman mentions that there were attempts in his time to combine QED (quantum electro-dynamics) and the weak force into a single theory. How is that going right now?

 

A: Good!  It’s the called “electro-weak theory”, and it’s now a big part of the “standard model”.  This is a bit over-simple, but in QED there’s a pretty natural place to plug in a mass term.  The photon (the force carrying particle for electromagnetism) has no mass, but the force carriers for the weak force (the Z and W bosons) do.  Once you plug in the mass, and do some surprisingly nasty math, the weak force falls right out.  In fact, if you were so inclined, you could describe the photon and Z boson as two states (a massive high-energy state, and a massless low-energy state) of the same particle!

Posted in -- By the Physicist, Particle Physics, Philosophical, Quantum Theory | 3 Comments

Q: What are integral transforms and how do they work?

Posted on July 14, 2011 by The Mathematician

Mathematician: If you have a function f(x) and a function k(x,s) then you can (as long as the product of f(x) times k(x,s) is integrable on the set X) always form another function of a new variable s as follows:

F(s) = \int_{X} k(x,s) f(x) dx

We have just “transformed” the function f(x) into the function F(s) via an “integral transform.” Why the hell would anyone want to do this? Well, the function F(s) is sometimes easier to work with than f(x) itself, or tells us interesting information about f(x) that it would be hard to figure out in other ways.

Of course, the interpretation of this new function F(s) will depend on what the function k(x,s) is. Choosing k(x,s) = 0, for example, will mean that F(s) will always be zero. This is pretty boring and tells us nothing about f(x). Whereas choosing k(x,s) = x^{s} will give us the sth moment of f(x) whenever f(x) is a probability density function. For s=1 this is just the mean of the distribution f(x). Moments can be really handy.

A particularly interesting class of functions k(x,s) are ones that produce invertible transformations (which implies that the transform destroys no information contained in the original function). This will occur when there exists a function K(x,s) (the inverse of k(x,s)) and a set S such that

f(x) = \int_S K(x,s) F(s) ds

that undoes the original transformation (or, at least, undoes it for some large class of functions f(x)).

Whenever this is the case, we can view our operation as changing the domain from x space to s space. Each function f of x becomes a function F of s that we can convert back to f later if we so choose to. Hence, we’re getting a new way of looking at our original function!

It turns out that the Fourier transform, which is one of the most useful and magical of all integral transforms, is invertible for a large class of functions. We can construct this transformation by setting:

k(x,s) = e^{-i x s}
K(x,s) = e^{i x s}

which leads to a very nice interpretation for the variable s. We call F(s) in this case the “Fourier transform of f”, and we call s the “frequency”. Why is s frequency? Well, we have Euler’s famous formula:

e^{i x s} = \cos(x s) + i \sin(x s)

so modifying s modifies the oscillatory frequency of cos(xs) and sin(xs) and therefore of k(x,s). There is another reason to call s frequency though. If x is time, then f(x) can be thought of as a waveform in time, and in this case |F(s)| happens to represent the strength of the frequency s in the original signal. You know those bars that bounce up and down on stereo systems? They take the waveforms of your music, which we call f(x), then apply (a discrete version of) the Fourier transform to produce F(s). They then display for you (what amounts to) the strength of these frequencies in the original sound, which is |F(s)|. This is essentially like telling you how strong different notes are in the music sound wave.

Below are a few other neat examples of integral transform.

The Laplace transform:

k(x,s) = e^{-x s}

This is handy for making certain differential equations easy to solve (just apply this transformation to both sides of your equation!)

The Hilbert transform:

k(x,s) = \frac{1}{\pi} \frac{1}{x-s}

This has the property that (under certain conditions) it transforms a harmonic function into its harmonic conjugate, elucidating the relationship between harmonic functions and holomorphic functions, and therefore connecting problems in the plane with problems in complex analysis.

The identity transform:

k(x,s) = \delta(x-s)

Here \delta is the dirac delta function. This is the transformation that leaves a function unchanged, and yet it manages to be damn useful.

Posted in -- By the Mathematician, Engineering, Equations, Math | 9 Comments

Q: How does reflection work?

Posted on July 4, 2011 by The Physicist

The original question was: How does reflection work (what happens on the reflective surface), why is the angle of incidence equal to the angle of reflection and can this be viewed both from particle and wave point of view?

Physicist: In a way, reflection can’t really be described as particle phenomena at all.  A solid object can bounce, but that’s just a flexing and un-flexing of the object.  An individual particle can’t bounce the same way, but due to its wave nature it can reflect.

Essentially, a reflective surface enforces some kind of restriction on the wave, usually that the wave must have zero amplitude at the surface.

For example, to derive the existence of echos (off of a rock wall or something) you declare (reasonably) that the perpendicular velocity of the air at the surface must be zero.  That is; air can flow along rock, but it can’t flow into or out of it.

For another example; it turns out that the electric field in conductive metals is zero (if it’s not, then the charges in the metal move to make it zero).  In a way mathematically almost identical to echos you can then describe light (an electromagnetic wave) reflecting
off of shiny metals.

It usually makes most people a little uncomfortable, but the best way to enforce the “zero boundary condition” (like in both examples above) is to:

1) pretend the surface isn’t there and then

2) describe the situation in terms of another wave coming through where the surface was that’s exactly the same as the incoming wave, but negative.

The result is that the new wave coming back at you cancels out the original wave at the location where there should be the reflecting surface.  So, the boundary condition is satisfied: the wave has zero value at the surface (whether that’s zero air movement, or whatever).

The negative wave that comes out doesn’t sound or look any different, and the original wave disappears (past the surface).  What we perceive in waves is frequency (“pitch” for sound, “color” for light), but the difference between the old and new waves is “phase”, which we don’t sense.

The important thing to keep in mind is that only what happens on the near side of the surface is real, everything on the other side is just a mathematical artifact, and (once the math is done) should be ignored.

Mathematically, as long as you restrict your attention to the left side, the following cases are exactly the same: 1) a wave reflecting off of a non-permeable surface and 2) no surface, but two waves, one positive, one negative, passing each other such that they exactly cancel. The red curve is the sum of the two waves.

Notice that this only applies to the component of the wave that’s perpendicular to the surface.  The part of the wave that runs parallel to the surface is unaffected.  That gives you exactly what you need for the angle of incidence and the angle of reflection to be equal.

Only the part of the wave perpendicular to the surface (blue) gets flipped. The part of the wave running parallel to the surface (red) is unaffected. Draw a picture, notice the similar triangles, and boom!: the angle of incidence equals the angle of reflection.

This has nothing to do with the question, but it’s interesting.  The “ignore the surface and pretend there’s something balancing on the other side” technique is useful all over the place.  For example, when something flies (birds, planes, etc.) it does so by pushing air downward, one way or another.

Pelicans, and many other birds, fly low over water to take advantage of the ground effect, which can be imagined in terms of the influence of the "reflected pelican" pushing air up. Also, there are fish involved.

Again, since air can’t move through a solid surface, you can model the fluid dynamics (“fluid dynamics” includes “air dynamics”) of something flying low over a surface with an identical “flying reflection”.  So while a bird pushes air downward, its “reflection” is pushing air up, with the net effect that no air moves through the surface.  The upward push of air manifests as the “ground effect” which is experienced by pilots and birds as a cushion of air that helps hold you up when you get close enough to the ground.

Even as a passenger, you can usually feel the ground effect just as your plane is about to touch down.

Posted in -- By the Physicist, Geometry, Philosophical, Physics | 2 Comments

Q: What does a measurement in quantum mechanics do?

Posted on June 29, 2011 by The Physicist

Physicist: This is a follow up of this post, that would’ve been too long and meandering with this included.  To sum up that post, a “measurement” is an interaction that exchanges information.

In the Copenhagen interpretation, what that measurement does is a magical rearrangement of the whole universe, faster than light.

More accurately (and here’s the answer), a measurement establishes an “entanglement” between the things involved.

A quick word about entanglement: Say you’ve got two marbles in a hat that are identical in every way, other than their color: red and blue.  You and a friend each take out a marble without looking at it.  You could have either one, but you don’t know which.  What you do know, is that if you have the red marble your friend will have the blue marble, and if you have the blue, they’ll have the red.  The marbles are correlated.  If you each look, you’ll find that you never have the same color.

Obviously, your marble is in one state: either it’s red or it’s blue.  In quantum mechanics however, a thing can be in multiple states, and amazingly enough, you can still have the same kind of correlation.  You have a marble that is both red and blue (a red/blue “super-position”), and so does your friend, and yet they are both correlated such that they always have opposite colors.  That is, just like in the non-quantum example, if you each look at your marble you’ll find you never have the same color.  This multiple-state-yet-still-correlated thing is called “entanglement”.  If you’re confused, then you’re awake.  Back to the question:

Imagine that, for some reason, you and a friend get some pitching machines and start chucking baseballs at each other.  Just to see if you can, you set up the machines so that they fire at the same time and the baseballs hit each other in mid-air.  Now, pitching machines aren’t perfect, so the balls won’t always take the same path, just one that’s more or less forward.  In particular, there’s no way to predict what angle they’ll hit each other at, and in what directions they’ll bounce apart.

After the collision there’s not a lot you can say about the trajectory of each ball.  One thing you can say for sure is that, regardless of the direction one ball flies, the other ball will fly off in the opposite direction.  After the collision their trajectories are correlated (maybe not perfectly, but follow me here).

Baseballs are pitched such that they bounce off of each other in mid air.

Now look at the same situation from a more “quantumy” perspective.  The pitching machines throw the baseballs, not in one of many slightly different trajectories, but in all of the possible slightly different trajectories.

Each baseball, rather than following a single path, takes a super-position of every possible path (in a cone). After the collision the balls are still in a super-position of every possible resulting path, but must be traveling in opposite directions. Correlated super-positions = entanglement.

Clearly the collision conveys information, so it is a measurement.  The information is pretty straight forward (“you are being hit by a baseball”), but it’s still informative.  Surprisingly, the effect of that measurement depends on your perspective.

From an outside perspective: both baseballs move toward each other in many, uncorrelated, paths.  A “baseball probability cloud”.  I say that they’re uncorrelated because even if you know which path one of the baseballs is taking, you still know nothing about the other.

When they collide and bounce apart, they’re still traveling along a super-position of many possible paths, but now they’re correlated.

Their collision (and mutual measurement) has entangled their states.

From an inside perspective: each state of each baseball thinks of itself as the only state.  An “inside perspective” means picking one state out of the many, and thinking about what it’s life is like (to be needlessly over-the-top exact; “…picking one bundle of indistinguishable states out of the many…”).

After it’s fired, if you look at just one state of the bottom baseball it looks “non-quantum” and follows one path. From its perspective the other ball is in a super-position of states. But, when they collide they measure each other, and suddenly see themselves and the other ball in just one state.  Note that each of the different states experience this.

Before they collide, one ball sees the other ball as being in many states.  When they collide they suddenly see the other ball as being in one state.  So, from an “inside” point of view, measurement looks like “wave function collapse“, one of the great weirdnesses of the Copenhagen interpretation (“collapse” = “all but one state disappears”).  When a ball bounces away from the collision it still sees itself going in one direction, and (since the balls always bounce in opposite directions) it’ll definitely see the other ball going in only one direction.

Their collision (and mutual measurement) has collapsed the state of the opposite ball (from the perspective of both balls).

But keep in mind that every state of both balls sees a (different) wave function collapse.  There’s nothing special about either ball; they’re both in many states.

Just for fun, a very outside perspective: Say you’re in another star system, and you can’t get any real information about what’s going on.  You see not just the baseballs in many states, but the people involved as well.  After a collision, the people running the machines see the baseballs as being entangled.  Now say one of them (Bob) tries to find one of the balls.  When he does, he suddenly knows where the other ball is.  Bob’s excited because he just experienced wave function collapse for the octillionth time that day.  Also, since the balls were entangled, he’s instantly “collapsed the wave function” of the other ball (he now knows where it is).

But, from your very outside perspective, Bob’s many states are searching for the ball’s many states.  Each of his many states eventually finds one of the ball’s many states.  Now, from far enough out, we can’t tell where each of Bob’s states finds the ball.  All we can say is that the wherever the ball is, that’s where Bob will find it.  That is; the state of the ball that bounced east from the collision will be correlated with the state of Bob that finds the ball to the east of the collision.  Both Bob and the ball are still in many states, but now they’re correlated.  By finding the ball, Bob (in his many states) is now entangled with it.

Even more awesome, since the baseballs were already entangled with each other, by entangling with one, Bob entangles himself with both.  That’s not too impressive from Bob’s perspective, but it can seem spooky from a very removed perspective.

Posted in -- By the Physicist, Entropy/Information, Philosophical, Physics, Quantum Theory | 14 Comments