Q: If you stood in the beam of a particle accelerator, what would happen?

Posted on June 25, 2011 by The Physicist

The original question was: Assuming you could avoid any other of the effects of being in an active particle accelerator tube,  How much damage would you expect by the particles smashing into you?  How much would the amount of mass within the particles effect your chances of living/dying?  And if you survived the impact, what kind of havoc would a mini black hole wreak inside you?

Physicist: If you took all of the matter that’s being flung around inside an active accelerator, and collected it into a pellet, it would be so small and light you’d never notice it.  The danger is the energy.

If you stood in front of the beam you would end up with a very sharp, very thin line of ultra-irradiated dead tissue going through your body.  It might possibly drill a hole through you.  You may also be the first person in history to get pion (“pie on”) radiation poisoning (which does the same thing as regular radiation poisoning, but with pions!).

When it’s up and running, there’s enough energy in the LHC beam to flash boil a fair chunk of person (around 10-100 pounds, depending on the setting of the accelerator).  However, even standing in the beam, most of that energy will pass right through you.  The higher the kinetic energy of a particle, the smaller the fraction of its energy tends to be deposited.  Instead, high energy particles tend to glance off of other particles.  They deposit more overall than a low energy counterpart, but most of their energy is carried away in a (slightly) new direction.

So instead of all the energy going into your body, the beam would glance off of atoms in your body, causing the beam to widen, and most of the energy would be deposited in whatever’s behind you (the accelerator only holds a very thin beam, so any widening will cause the beam to hit the walls).

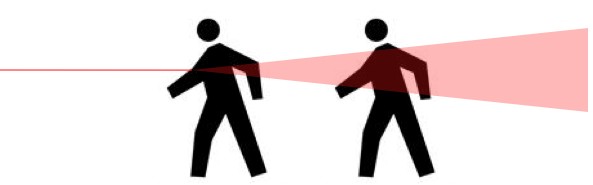
CERN's motto "CERN: Don't be a hero", is in reference to the fact that if you see someone in the beam, stepping in front of them just makes things worse.

If the LHC ever manages to create a micro black hole, that micro black hole should “pop” immediately after being created.  The smaller a black hole, the faster it loses mass and energy to Hawking radiation.  And a minimum-mass black hole radiates so fast that it’s easier to describe as an explosion (small explosion).  Most models predict that the LHC won’t come remotely close to creating a minimum-mass black hole, but one or two of the farther fringes of string theory say “maybe”.  If the LHC does create a tiny black hole, it would deposit all of the energy of two TeV particles slamming together (which has all the fury of an angry ant stomping) in the form of a burst of radiation.

Update (6/27/2011): A concerned reader pointed out that there is at least one known particle-beam-accident.  A Russian nuclear scientist named Anatoli Bugorski, who at the time was working through his PhD at the U-70 synchrotron (which has approximately 1% of the LHC’s maximum power), was kind enough to accidentally put his head in the path of a proton beam.

He’s doing pretty well these days (considering).  The damage took the form of a thin strip of intense radiation damage, that killed all the tissue in a straight line through the left side of his head.  Despite the fact that that line passed through a lot of brain, he still managed to finish his PhD.

Posted in -- By the Physicist, Particle Physics, Physics | 20 Comments

Q: What exactly is the vacuum catastrophe and what effects does this have upon our understanding of the universe?

Posted on June 16, 2011 by The Physicist

Physicist: The vacuum catastrophe is sometimes cited as the biggest disagreement between theory and experiment ever.  They disagree by a factor of at least 10107.

According to quantum field theory the energy of empty space can’t quite be zero.  In fact, QFT gives us an exact value for how much energy empty space should have.  Although we can never access that energy, it does have a gravitational effect.

One of the (many) things the Voyager probes did was allow us to estimate how strong those gravitational effects are.  Unfortunately, they determined that the theoretical predictions are way, way, way off (too high).

There’s a short paper here aimed at the undergraduate physics crowd that covers this better than I do.

It’s a catastrophe because QFT is otherwise a stunningly accurate theory (the most accurate ever, by far).  But, at the end of the day, you have to fall back on observation, so something about our favorite theory is wrong.

One result of the Heisenberg Uncertainty Principle is that it’s impossible for a system to be in a zero-energy state.  In a nutshell: if a particle definitely has zero energy, then it’s definitely not moving and its momentum is zero.  However, to get that level of certainty you need the position to be completely uncertain and (for various reasons) that’s untenable.  You can run through this mathematically, and you find that systems always have just a tiny bit more than zero energy, and that that energy is proportional to \frac{\omega}{2}, where \omega is the frequency of the particle/system in question.  That little bit of energy is called the “ground state energy” or just “ground energy”.

The same thing applies to all particle fields, but rather than generalize, I’ll just talk about light: the electromagnetic (EM) field.  It turns out that every frequency of the EM field, at every point in space, is its own tiny system (not at all obvious; that falls out of the math).  As a result, instead of a tiny ground state energy for a single system, in any given region of space you have lots of systems.  These form the ground state energy density, which is more commonly known as the “zero point energy”.

As a quick aside, a lot of people get very excited about zero point energy, but shouldn’t.  Setting aside the fact that harvesting it would violate the Uncertainty Principle (which is set in stone pretty good), to generate usable energy you still need to drop things from high energy states to low energy states.  For example, there’s a tremendous amount of potential energy to be gained by dropping all of the ocean’s water to the bottom of the ocean (a waterfall as tall as the ocean is deep would generate a lot of hydroelectric power).  Of course, first we just need to pump all the water out.  Then we can gain energy by pouring it all to the bottom (so, the net energy gain is at best zero).

Back to the point: So there’s a ground state energy for each frequency of light. Looking at all the frequencies up to \Omega you find that the ground state energy density is proportional to \Omega^4 (again, not obvious).

But there are a lot of frequencies out there!  As far as we know, there may be no upper limit, which would imply that the ground state energy is infinite.  There are a lot of ad hoc estimates (that tend to be extremely high), based on the highest energy photons we can make with our accelerators, or the highest energy photons observed, or the highest energy photon it even makes sense to consider (if the frequency is too high, the wavelength is short enough that space gets “grainy”… sort of).  All of these estimates maintain that the zero point energy is stupefyingly huge.

However, all energy and matter creates gravity, so you’d expect that all that extra stuff would affect how gravity works.  Specifically, you’d expect the velocity of orbiting objects to all be about the same, regardless of the size of the orbit (still: not obvious).  But, to the best of our ability to measure (which is pretty good), no effect has been seen at all in terms of the movement of stars and planets and whatnot.

So why not just abandon the whole zero point energy idea?  Why not say: “it’s clearly not around, so let’s move on”?  Because you can detect it!  Curveball!

The “Casimer effect” and a recent experimental set up to measure it. Normally the pressures of the (nearly) virtual particles around us balance out. But between two surfaces the lower frequency (longest wavelength) wave functions can’t exist, so they can’t add to the pressure. As a result the outside pressure is higher, and the surfaces are pushed together.

The electric field inside of a conductor is zero (in a super-conductor at least).  This principle is responsible for things like the shininess of metal and Faraday cages.  In between two conducting surfaces the electric field can only assume wavelengths shorter than the distance between the plates (and thus only frequencies above a certain cut-off), because the plates nail down the field by forcing it to be zero.

This is a little like saying you’d expect to find big, low-frequency, waves in the ocean, but not in a cup.

Since the region in between the conducting surfaces is missing all the “tiny systems” corresponding to those low freuencies, there’s a slightly lower energy density between two conducting surfaces than outside of them (never mind that both densities may be huge), and this manifests as a tiny pressure that pushes the surfaces together.  If there were no zero point energy at all, then you wouldn’t see this effect.

So, just like quantum field theory predicted, there is some ground state energy (1 point for QFT).  However, the theory also predicts that there should be so much energy that its gravitational effects would overwhelm the gravity of everything else (whoops).

As far as what this means for our understanding of the universe: we’re missing something.  But this is old-hat for scientists.  As a people, we’re used to dealing with unknowns and weird experimental results.  It’s just that, in physics at least, the last century has been one big prediction/verification win after another.  A stumbling block like this stands out because we’ve been doing so well.

The vacuum catastrophe may lead to another big paradigm shift, or a slight correction, or who knows.  Other small weirdnesses, like nuclear decay and Mercury’s orbit, have led to the creation of entirely new fields, like particle physics and general relativity.

We’re probably just not taking something into account, but it’s a big something whatever it is.

Posted in -- By the Physicist, Astronomy, Particle Physics, Physics, Quantum Theory | 22 Comments

Q: What is a “measurement” in quantum mechanics?

Posted on June 13, 2011 by The Physicist

Physicist: Any interaction of any kind that conveys information is a form of detection.

This question crops up frequently in conjunction with the “Copenhagen interpretation”.

The Copenhagen interpretation of quantum mechanics (which comes in a couple different flavors) is generally stated as “a thing is in a super-position of states until it’s measured”.  Some people (including very few physicists) have come to the conclusion that “measurement” means “measured by something conscious, and also we’re all part of the same energy field, so we’re psychic, and modern science is only now coming to understand what eastern philosophers have known for millennia”.

Just to be clear, the Copenhagen interpretation is a bottomless font of problems and paradoxes, of which the “measurement problem” is one of the more interesting (but still: one of many).  Luckily, since Copenhagen is based on an assumption (“things are in many states until measured”) that never needed to be made, isn’t well-defined, and is in no way supported by any kind of evidence, it can be abandoned giving rise to the Many Worlds Interpretation.  Sorrowfully, it’s often found unabandoned (particularly in new age literature).

More often (in sciency circles), Copenhagen is described in terms of a small system (a few particles) in many states interacting with a larger system that’s in only one state, as “big systems” like people appear to be.  Somehow that interaction “collapses the wave function”, and only one of the many states of the small system persists.

But you may have noticed that experiments like the quantum mechanic’s mainstay, the double slit experiment, can be done in air.  That is, you don’t have to remove the air (a very large system) from around the double slits before you do the experiment.  The photons (one photon = small system) involved are definitely interacting with air molecules, and yet they clearly continue to demonstrate super-position (being in multiple states).  You can even do the double slit experiment off of a mirror, which is definitely a big system.  So it’s not just an interaction between a small, many-states, system and a large system that defines a “measurement”, it’s a bit more subtle.

A measurement is best defined as anything that gives you information.  And information is what allows you to narrow your choices, or at least refine your probabilities.

For example, when light passes through sugar-water its polarization rotates (you can try it if you like, but for this post don’t be concerned about why it works).  But if you don’t know anything about what the polarization of the light was before it entered the sugar-water, you won’t know anything about the polarization afterward.  It’s an interaction, but not a measurement.  It’s like asking “if I take a coin and turn it over, will it be heads or tails?”.  Without knowing what it was beforehand, there’s no new information about what it will be afterwards.  In the sugar-water case, this manifests as a conservation of states: if the photon enters the sugar-water in multiple states, it leaves in multiple states (just not the same states).

A polarizer on the other hand definitely performs a measurement.  If light goes through, then it’s polarized in the same direction as the polarizer, and if it doesn’t, then it’s not.

Left: the "Faraday effect" occurs when light passes through a "twisty" material, like sugar. The polarization gets rotated, but not measured. If a photon enters in many states, it remains in many states. Right: A polarizer filters light of a certain polarization. If the photon is in multiple polarization states then the polarizer forces the photon to (from our perspective) "choose" between states. Either it's polarized correctly and passes through, or it's polarized incorrectly and is stopped.

But describing a measurement in terms of information leads to another, possibly nightmarish, question: Is it possible to do a “partial measurement”, that gets only a little information?

If you’ve ever listened to a bus or train announcement you know that it’s possible to get more than none, but far less than all, of the information you’d like.  For example; after an announcement you may decide that there’s a 70% chance the train is late, a 25% chance it’s on time, and a 5% chance that someone with a crippling speech defect has violently taken over the PA system.  This is a partial measurement, because a full measurement would take the form of 100% probabilities.  As in; “the train is definitely, 100%, late”.

Happily, the same is true in quantum mechanics, and it’s extremely useful!  For example you can use partial measurements to make “(usually) interaction free measurements”, which is sometimes called “seeing in the dark“.  So, you can refine the states of a system without destroying its super-position-ness.

In the double slit experiment you usually set up the apparatus so that there’s a 50% chance of each photon going through either slit (the video in that link is the best explanation I’ve seen, but it jumps the rails a bit around minute 4).  “50/50” is just another way of saying “there’s no information about which slit the photon’s going through”.

Double slit set up.

But there are many ways to gain some information about which slit the photon goes through.  For example, you can move the light source closer to one slit, or put some darkened glass over a slit to absorb some photons.  Either way, once a photon has passed through the slits you have some idea of which one it went through, but not certainty.  As in: “it probably went through the slit that isn’t covered by the darkened glass, but maybe not”.

Any way that you do it, a partial measurement affects the interference pattern.  What’s very exciting is that you can slide cleanly from “no measurement” (50%/50%) to “total measurement” (0%/100%).

The more you know which slit the photon passes through, the weaker the interference pattern. By the time you're 100% certain which slit the photon goes through (by covering the other or something) you're left with a bump under the one active slit, which is exactly the not-quantum-weirdness result you'd expect.

So, while it’s a huge pain to define “measurement” in a physical context, you can define it pretty readily in a mathematical/information-theory way as “an interaction that conveys information, allowing you to be more certain about what the states are”.

Just to be clear, there doesn’t need to be a person doing a measurement.  “Measurement” and “quantum mechanics” may remind you of scientists in labs, but any interaction that conveys information (which in day to day life is basically all of them) is a measurement.  If a tree falls in the forest, and no one’s there to see it, the tree and ground still measure each other.

Posted in -- By the Physicist, Entropy/Information, Physics, Quantum Theory | 28 Comments

Q: How close is Jupiter to being a star? What would happen to us if it were?

Posted on June 8, 2011 by The Physicist

The original question was: I have heard Jupiter referred to as a failed star.  That if the cosmic chaos of the early solar system had worked out a little different, and Jupiter had gotten a bit more mass, it might have been able to light the fusion engine and become a star.

Two questions.

How close was Jupiter to becoming a star?

If something really big slammed into Jupiter today, could it trigger nuclear fusion?

Ok and a third question.  If Jupiter did in fact get slammed with something big enough to trigger nuclear fusion, and it became a star, how long would it take to substantially alter the ability for earth to sustain life as we know it?

Physicist: That is a really cool question!

I heard the same thing a while ago, but Jupiter is a long way from being a star.  That estimate was based on some old nuclear physics (like 1980’s old).  By being awesome, and building neutrino detectors and big computers, we’ve managed to refine our understanding of stellar fusion a lot in the last few decades.

Although the material involved (how much hydrogen, how much helium, etc.) can change the details, most physicists (who work on this stuff) estimate that you’d need at least 75-85 Jupiter masses to get fusion started.  By the time a planet is that large the lines between planet, brown dwarf (failed star), and star get a little fuzzy.

So, for Jupiter to become a star you’d need to slam so much additional mass into it, that it would be more like Jupiter slamming into the additional mass.

If you were to replace Jupiter with the smallest possible star it would have very little impact here on Earth.

There’s some debate over which star is the smallest star (seen so far).  OGLE-TR-122b, Gliese 623b, and AB Doradus C are among the top contenders (why is every other culture better at naming stars?), and all weigh in around 100 Jupiters.  They are estimated to be no more than 1/300th, 1/60,000th, and 1/1,000th as bright as the Sun respectively.  So, lets say that Jupiter suddenly became “OGLupiter” (replaced by OGLE-TR-122b, the brightest of the bunch, and then given the worst possible name).  It would be a hundred times more massive, 20% bigger, a hell of a lot denser, and about 0.3% as bright as the Sun.

At it’s closest Jupiter is still about 4 times farther away from us than the Sun, so OGLupiter would increase the total energy we receive by no more than about 1 part in 5 thousand (about 0.02%).  This, by the way, is much smaller than the 6.5% yearly variation we get because of the eccentricity of Earth’s orbit (moving closer and farther away from the Sun over the course of a year).  There would be effectively zero impact on Earth’s life.

There are examples of creatures on Earth that use the moon for navigation, so maybe things would eventually evolve to use OGLupiter for navigation or timing or something.  But it’s very unlikely that anything would die.

OGLupiter would be around 80 times brighter than a full moon at its brightest, so for a good chunk of every year, you’d be able to read clearly at night.  It would be very distinctively red (being substantially colder than the Sun), and it would be clearly visible even during the day.

Posted in -- By the Physicist, Astronomy, Physics | 135 Comments

Q: Can you fix the “1/0 problem” by defining 1/0 as a new number?

Posted on June 2, 2011 by The Physicist

The original question was: I’ve been relearning some things about imaginary numbers and the concept behind the number i got me thinking about something else. Is there a reason that the quantity 1/0 could not be defined in a similar way to i, so that functions could a real component, imaginary component, and an undefined component? If so, what implications would this have to mathematics? I can’t see it being very useful but I was curious to see what you think.

Physicist: If that worked it would be extremely useful. However, it just doesn’t jive with the axioms of arithmetic.
People in the math biz are always making up place holders for things that aren’t known or, in some cases, can’t exist. Euler (pronounced “Oiler”, as in “one who oils”) wanted to come up with a number system that included a solution to x2+1=0. He called that solution “i “, for “Imaginary number” or possibly “Incredibly awesome number” (I think it’s the latter).

As it happens, there are no problems involved with defining i.  In fact, it really cleans up a lot of math.  1/0 on the other hand is kind of a train wreck.

Define Q (for “Quite a bit more awesome than i“) as the solution to 0x=1. That is, define Q as “1/0”, so it’s the “multiplicative inverse” of 0.  Right off the bat there’s a problem:
\begin{array}{ll}1=Q\cdot 0\\\Leftrightarrow 1=Q\cdot (1-1)\\\Leftrightarrow 1=Q-Q\\\Leftrightarrow 1=0 \end{array}

This is because zero is defined as “x-x” for any number or variable x.  So by assuming 1=Q\cdot 0 (and the laws of arithmetic) you reach an impossible conclusion!

You could try to patch this problem, for example by declaring that Q-Q\ne 0.  Even so:

\begin{array}{ll}1=Q\cdot 0\\\Rightarrow 1\cdot 0=Q\cdot 0^2\\\Rightarrow 0=Q\cdot 0\\\Rightarrow 0=1 \end{array}

Again, by defining 1=Q\cdot 0 to be true, you’re led to a contradiction.  Mo’ logic, mo’ problems.  You could fix this problem by declaring that associativity doesn’t apply to Q.  That is, (Q\cdot 0)\cdot 0 \ne Q\cdot (0\cdot 0).  Losing associativity is a big deal though.  Without it you can barely do anything.

You can keep going, finding more problems and declaring more “fixes”, but in short order you’ll find that by the time you’re done patching things you’ll have more problems, exceptions, and caveats than just “1/0 is undefined”.

Best to just leave 1/0 undefined.

Posted in -- By the Physicist, Conventions, Logic, Math | 30 Comments

Q: How can we have any idea what a 4D hypercube or any n-D object “looks like”? What is the process of developing a picture of a higher dimensional object?

Posted on May 31, 2011 by The Physicist

Physicist: Math.  Math all over.

A picture of a 3D object is a “projection” of that object onto a 2D page.  Projection to an artist means taking a picture or drawing a picture.  To a mathematician it means keeping some dimensions and “pancaking” others.

So when you take a picture the “up/down” and “left/right” dimensions are retained, but the “forward/back” dimension is flattened.  Mathematicians, being clever, have formalized this into a form that is independent of dimension.  That is, you can take an object in any number of dimensions and “project out” any number of dimensions, until it’s something we can picture (3 or fewer dimensions).

Top: An object in 3 dimensions. To see it, cross your eyes by looking “through” the screen until the two images line up. Middle: By “projecting out” the z axis (toward/away) the object is collapsed into two dimensions. This is what cameras do. Bottom: By projecting out the y axis (up/down) the object is collapsed again into 1 dimension. This is akin to what a 2D camera would see, photographing from below.

We’re used to a 3D-to-2D projection (it’s what our eyeballs do).  A 4D-to-2D projection, like in the picture above, would involve 2 “camera/eyeball like” projections, so it’s not as simple as “seeing” a 4D object.

As for knowing what a 4D, 5D, … shape is, we just describe its properties mathematically, and solve.  It’s necessary to use math to describe things that can’t be otherwise pictured or understood directly.  If we had to completely understand modern physics to use it, we’d be up shit creek.  However, by describing things mathematically, and then following the calculations to their conclusions, we can get a lot farther than our puny minds might otherwise allow.

Lines, squares, cubes, hyper-cubes, hyper-hyper-cubes, etc. all follow from each other pretty naturally.  The 4D picture (being 4D) should be difficult to understand.

For example, to describe a hypercube you start with a line (all shapes are lines in 1D).

To go to 2D, you’d slide the line in a new direction (the 2nd dimension) and pick up all the points the line covers.  Now you’ve got a square.

To go to 3D, you’d slide the square in a new direction (the 3rd dimension) and pick up all the points the square covers.  Cube!

To go to 4D, same thing: slide the cube in the new (4th) direction.  The only difference between this and all the previous times is that we can no longer picture the process.  However, mathematically speaking, it’s nothing special.

Answer gravy: This isn’t more of an answer, it’s just an example of how, starting from a pattern in lower dimensions, you can talk about the properties of something in higher dimensions.  In this case, the number of lines, faces, etc. that a hyper-cube will have in more than 3 dimensions.

Define e_N as an N dimensional “surface”.  So, e_0 is a point, e_1 is a line, e_2 is a square,e_3 is a cube, and so on.

Now define e_N(D) as the number of N-dimensional surfaces in a D-dimensional cube.

For example, by looking at the square (picture above) you’ll notice that e_0(2)=4, e_1(2)=4, and e_2(2)=1.  That is, a square (2D cube) has four corners, four edges, and one square.

The “slide, connect, and fill in” technique can be though of like this: when you slide a point it creates a line, when you slide a line it creates a square, when you slide a square it creates a cube, etc.  Also, you find that you’ll have two copies of the original shape (picture above).

So, if you want to figure out how many “square pieces” you have in a D-dimensional cube you’d take the number of squares in a D-1 dimensional cube, double it (2 copies), and then add the number of lines in a D-1 dimensional cube (from sliding).

e_N(D) = 2e_N(D-1) + e_{N-1}(D-1).  Starting with a 0 dimensional cube (a point) you can safely define e_0(0) = 1.

The values of e_N(D) arranged to make the pattern clearer. You can use the pattern to accurately predict what the cube in the next dimension will be like.

It’s neither obvious nor interesting how, but with a little mathing you’ll find that e_N(D) = {D \choose N} 2^{D-N} = \frac{D! \,2^D}{N!(D-N)! \,2^N}, where “!” means factorial.  So, without ever having seen a hypercube, you can confidently talk about its properties!  For example; a hypercube has 8 cubic “faces”, 24 square faces, 32 edges, and 16 corners.

Posted in -- By the Physicist, Geometry, Math, Philosophical | 24 Comments