Q: Is it possible to destroy a black hole?

Posted on May 29, 2011 by The Physicist

The original question was: Aside from Hawking radiation, is it possible to destroy a black hole? Specifically, could you rotate a black hole fast enough that it was flung apart? Also, assuming that m is the mass necessary for a black hole (though I realize they’re more a density than mass thing), and you had a black hole of, say, 10m, could you throw some amount of anti matter at it (say 5m) to rip it apart without simply converting all it’s matter into energy?

Physicist: Black holes are a little tricky.  Rather than thinking of them as solid objects, it’s better to think of them as “messed up patches of geometry”.  Destroying a black hole is just as difficult as destroying any patch of space.  So, if by setting off a bomb you could change how rulers measure distance in a particular region of space, then you could affect a black hole.

Chucking anti-matter into a black hole would actually make it bigger.  Anti-matter, as the named doesn’t imply, is made of the same “stuff” as ordinary matter.  That is, if you were made of anti-matter, everything about you would be exactly the same (there are some subtleties with regard to neutrino emission, but who notices that?).  The big thing that makes matter and anti-matter different is that bringing them together makes them cancel each other out, dumping all of their intrinsic energy (of the “E=MC2” variety) into a big boom.

Even if it did contact some matter inside, there’s no direction the explosion could go that doesn’t point toward the center.  Beyond the event horizon all directions point down (and that’s messed up geometry).

Another way to look at it is; gravity is generated by both matter and energy, so converting a black hole’s matter into energy wouldn’t change much.  You still have the same amount of matter/energy, and thus the same amount of gravity.

A spinning black hole can (in theory) produce a naked singularity, and maybe there’s something that can be done with that (most theories don’t have many definitive things to say about singularities), but probably not.  Black holes are pretty tough.

Posted in -- By the Physicist, Physics | 48 Comments

Q: Why does the Earth orbit the Sun?

Posted on May 24, 2011 by The Physicist

The original question was: What exactly causes the Earth’s rotation and revolution?  Does this occur due to centripetal force and the lack of friction to stop the Earth from spinning? IE- Newton’s First Law? If so, where did this centripetal force come from? Was it a product of this rock being hurled through space and stuck in the Sun’s pull? As for the rotation, I don’t even have a guess. Are there planets that don’t revolve at all, or is that a necessity?

Physicist: I’ll break this down into two questions: “Where does the rotation originally come from?” and “Once the a planet is in orbit, what keeps it there?”

Where does the rotation originally come from?: The original yearly rotation of the Earth around the Sun (orbital rotation), as well the daily rotation of the Earth about it’s own axis (just “rotation”) is essentially dumb luck.

If you hold out any object and toss it in the air, you’ll find that it’s almost impossible to toss it in such a way that it doesn’t turn at all.  The same is true of stellar nebulae (the gigantic clouds of gas and dust that condense to form stars and planets).  They always have at least a little bit of swirl and spin.

As the cloud that became our solar system collapsed inward, the mass settled into a spinning disc with a big bump in the middle (the Sun), and that disk began collapsing even more to form the planets.  This process is called accretion, and you can see it at work over and over again.

When stuff collapses it tends to form a central ball and a disk.

There aren’t any non-spinning planets, but the speed that they spin varies widely.  Jupiter’s day is only 10 hours long, while Venus’ is around 240 Earth days long.  How fast and in exactly what direction a planet will end up spinning is a fiendishly complicated problem.  Some of it is determined by the flow of the gas and dust of the “proto-planetary disk” (which is fairly simple), which is why the orbits and rotations of every planet in the solar system orbits and rotates in roughly the same direction.

Since the Earth orbits the sun in the same direction that it rotates, when it's morning (6 am) you're standing on the "front side" of the Earth.

But once the ball gets rolling (so to speak) you find yourself with a solar system full of big rocks on slightly different orbits slamming into each other, and changing each others rotations.  For example, the Earth’s moon was (most likely) created by a stupendous collision with something Mars-sized that “splashed” the moon into orbit.  That impact, as well as tidal effects from the moon itself, have radically changed the length of the day on Earth.  Uranus is also believed to be the victim of an even bigger collision that tilted it’s rotation axis around 98° from it’s orbital axis (the direction perpendicular to its orbit), and dramatically changed the length of it’s day.  We can’t say by how much; no one saw what it was like before.

So, in general, things spin because they collapse from very large clouds of stuff that were spinning (just a little) already.  If the cloud hadn’t been spinning, then all of the mass in the solar system would have fallen all the way into the Sun.  Instead, a mere 99.86% of the solar system’s mass is in the Sun.

Once a planet is in orbit, what keeps it there?: Gravity pulls the Earth in, and centrifugal force holds it out.*  The centrifugal force on the Earth is just a result of the Earth moving in a curved path around the Sun.  It doesn’t slow down because there isn’t any friction.  After all, in space, there’s nothing to have friction with.  Why exactly an orbit is stable involves a short romp in math town.

Gravitational force, Fg, is given by F_g = -\frac{GMm}{R^2}, where G is the gravitational constant (dictates how strong gravity is), M is the star’s mass, m is the planet’s mass, and R is the distance between the planet and star.  It’s negative because it’s trying to decrease R.  You can use this to find the gravitational potential, Ug, by taking the anti-derivative: U_g = -\frac{GMm}{R}.  Force is the negative of the derivative of potential, which is fancy-speak for “stuff wants to fall downhill”.

Centrifugal force, Fc, is given by F_c = \frac{mv^2}{R}, where m and R are the same and v is the “tangential velocity” (how fast the planet is moving around the star, and not counting motion toward or away from the star).  There’s a handy way to rewrite this in terms of angular momentum.  Angular momentum, L, is always constant and (in this case) is given by L=mRv.  Re-writing Fc in terms of L gives: F_c=\frac{m}{R}v^2=\frac{m}{R}\left(\frac{L}{mR}\right)^2=\frac{L^2}{mR^3}.  You can use this to find the “centrifugal effective potential”, Uc.  “Effective” is just a physicist’s way of saying “I know, I know; the centrifugal force isn’t a ‘real’ force.  Just be cool for, like, two minutes.”.  U_c=\frac{2L^2}{mR^2}

Looking at the total potential, U=Ug+Uc, it becomes clear why orbits can be stable.  In order to picture forces better physicists will sometimes draw “potential diagrams”.  A potential diagram is just an intuitive way of describing energy and, in turn, forces.  To understand it, imagine putting a marble on the line and think about how it will roll.  In the picture below the marble will roll to the left, but no too far.

The total potential curve in terms of distance to the Sun. When a planet gets too close to the Sun the centrifugal force "rolls it away", and when it gets too far away the gravitational force "rolls it back". A stable or "bound" orbit is one without enough energy to roll out of the pit. This diagram helps explain why it's so hard to fall into orbit around something: If you start from far away, you have enough energy to get back there.

An orbit is stable when the energy of a planet is “cupped” by the total potential.  If it gets too far out the gravity pulls it back, and if it gets too close the centrifugal force pushes it back out.

Also, as if you needed another reason to be excited about living in this universe, orbits are only stable in two and three dimensions.  The force of gravity drops in the same way that the intensity of light or sound drops off (in our case: 1/R2), so if the dimension of your space is D, then the force of gravity is F_g = -\frac{GMm}{R^{D-1}}.  This yields a gravitational potential of  U_g = -\frac{GMm}{(D-2)R^{D-2}} when D≥3, and U_g=GMm\ln{(R)} when D=2.

Gravity gets weaker, faster, the higher the dimension. In 1 dimension there's no circular movement and no orbits. In 2 and 3 dimensions the forces balance such that there are stable orbits. In 4 dimensions an object will either fall directly in or fly away forever (depending on its angular momentum). And in 5 or more dimensions gravity wins if an object is too close and centrifugal force wins if it's too far.

For small dimensions (2 and 3) the centrifugal force is stronger for small R and gravity is stronger for large R, which yields stable orbits.  For large dimensions (5 and up) gravity is stronger for small R and centrifugal force is stronger for large R, so the orbit is always trying to fly apart, one way or another.  In 4 dimensions the forces get stronger and weaker at the same rate (~1/R3), so if one is stronger than the other it’s always stronger.

*This isn’t technically true.  Technically the planet is moving in a straight line through curved spacetime, and experiences no centrifugal acceleration.  But whatevs.

Posted in -- By the Physicist, Astronomy, Equations, Physics | 63 Comments

Q: If you suddenly replaced all the water drops in a rainbow with same-sized spheres of polished diamond, what would happen to the rainbow? How do you calculate the size of a rainbow?

Posted on May 18, 2011 by The Physicist

Physicist: A normal rainbow is created when light enters a water droplet, bounces once off of the far side, and comes back out.

Diamond “droplets” however don’t make rainbows.  In order to get a rainbow that exists, and isn’t in a tiny ring right around the sun (where it’s drowned out), the light has to bounce three times inside the droplet.  By then it’s so dim that it’s unlikely anyone could see it.  But if you could: it would form an arc about 50° from the “anti-solar direction” (the direction exactly opposite the sun; where your shadow is).  For comparison, an ordinary rainbow is an arc about 40° around the anti-solar direction.  If it doesn’t make plenty of sense why a rainbow is angle-dependent, why not swing by the first rainbow post?

You can figure out where rainbows should be by thinking about how light bounces in a sphere and applying “Snell’s law” (named after the horrifically named “Willebrord Snellius“).  Then you can figure out what direction the light will ultimately go by adding up how much it turns from each interaction.

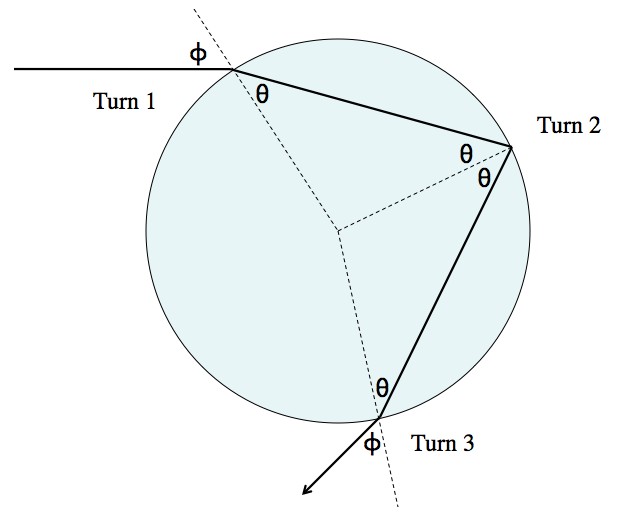
The set-up for a single-reflection rainbow. The light turns (in the same direction) three times: when entering, reflecting, and leaving.

Turn 1: When light enters the droplet it turns because of “refraction“.  The exact amount is given by Snell’s gross-sounding law.  If the index of refraction of the air is NA and the index of refraction of the water is NW, then: N_A \sin{(\phi)} = N_W \sin{(\theta)}.  It so happens that NA = 1 (well… 1.0003) and NW ≈ 1.3.  NW is slightly different for different colors, which is ultimately what gives rise to rainbows.  It takes a minute or two of pondering, but the light beam will turn to the right by an angle of (\phi - \theta).  First, imagine that \theta is zero, so the beam is pointing straight at the center of the drop.  That’s a turn of angle \phi (by opposite angles).  Now increase \theta and the amount of the turn decreases.  (\phi - \theta).

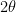Turn 2: Since the radius of the droplet is fixed, the path of the light and the radial lines form an isosceles triangle.  There’s another \theta!  Since the incoming and reflected angles have to be the same you get one more \theta.  If the beam were to have come straight back on itself that would’ve been a turn of 180°.  But it falls short of that by 2\theta.  So, the second turn is to the right again by an angle of (180-2\theta).  If there are R reflections then the total turning angle will be R(180-2\theta).

Turn 3: Snell’s did-you-sneeze-or-are-we-talking-about-optics law works the same way forward and backward.  That is; the angles are the same going in or coming out.  So, turn 3 is also by an angle of 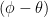(\phi-\theta).

The total angle, A, is the sum of the three turns: 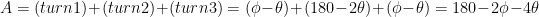A=(turn1)+(turn2)+(turn3)=(\phi-\theta)+(180-2\theta)+(\phi-\theta)=180-2\phi-4\theta.  Snell’s law can then be used to solve for \theta:

\begin{array}{ll}N_W \sin{(\theta)}=N_A \sin{(\phi)}\\\Rightarrow \sin{(\theta)}=\frac{N_A}{N_W} \sin{(\phi)}\\\Rightarrow \theta=\arcsin{\left(\frac{N_A}{N_W} \sin{(\phi)}\right)}\end{array}

So, the total turning angle is: 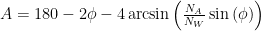A=180-2\phi-4\arcsin{\left(\frac{N_A}{N_W} \sin{(\phi)}\right)}

And allowing R reflections: 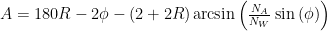A=180R-2\phi-(2+2R)\arcsin{\left(\frac{N_A}{N_W} \sin{(\phi)}\right)}

\phi, by the way, mostly just describes where on the drop the light initially hits.  In a second there’ll be a colorful graph that doesn’t make much sense.  So consider this:

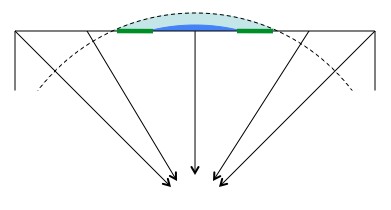
If a beam turns 180°, it’ll come right back at you.  If it turns 120° it’ll form a 60° arc, and if it turns 240° it’ll still form a 60° arc.  That’s a little confusing, so when you want to figure out how big a rainbow will be, quickly draw a picture to see what kind of angle the rainbow will make around the solar direction (toward the sun) or anti-solar direction (away).

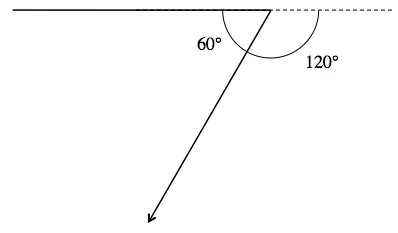
Whatever the total turn, just ask "how close is this to coming back or continuing forward?" In this picture a rainbow is made by light that turns 120°, so you can expect it to apear in a 60° arc around the anti-solar direction. 350° gives a 10° arc around the sun, 200° is a 20° arc around the anti-solar direction, ... Ordinary rainbows are created by light that turns 140° (picture below), and they appear in a 40° arc around the anti-solar direction.

Now check this out!

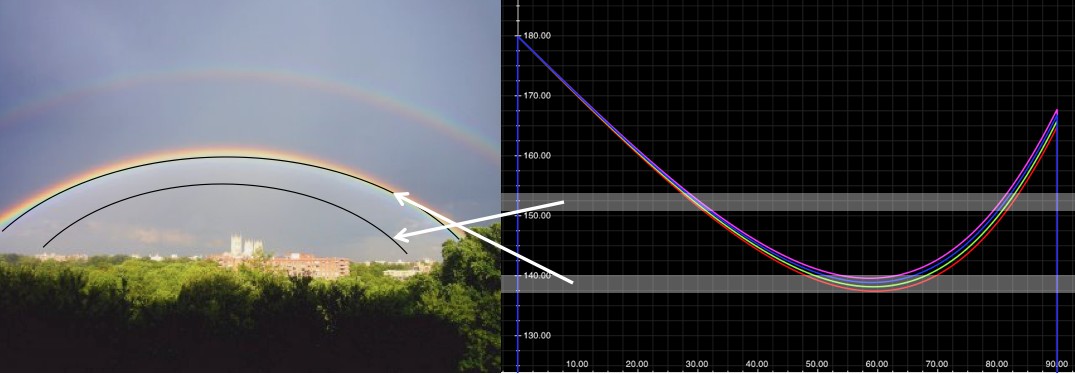
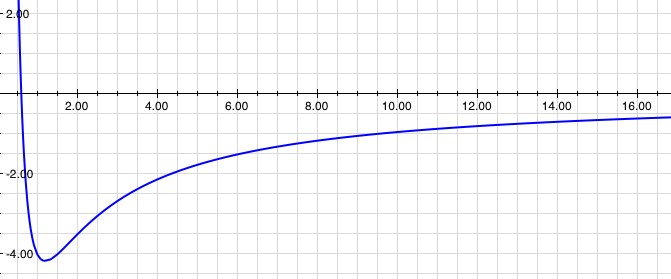
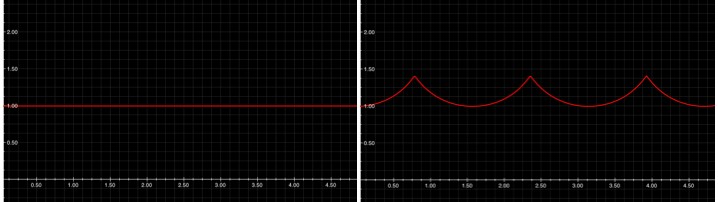
(click to enlarge) Different colors have different minimum turning angles. Red can turn as little as 138°, but the other colors all turn more. So at 138° you can only see red. At 140° all the colors are present, but purple is the most common. Inside the rainbow, between 140° and 180°, there's a fairly even mix of colors so you see white.

The index of diffraction is different for different materials, but it also changes for different colors of light (different frequencies).  For water you can find them here.  By graphing the total turning angle (vertical axis) vs. \phi (horizontal axis) for several colors you can immediately see at what angle the rainbow will show up.  In the graph above the red curve bottoms out lower than the other colors, so at 138° you’ll find red and nothing else.  A little higher and you have mostly greens and not much else.

To see this, enlarge the picture above, get a pencil, and, holding it level, move it up the graph.  You’ll notice that at various angles one color will be in contact with the top of the pencil for a far greater range than the other colors.  Hence, at that angle a particular color will be far more common than the others.

In general, in these graphs, a rainbow will show up whenever there’s a minimum (for a maximum you’d need a really weird material that doesn’t follow Snell’s law).  So, without graphing lots of colors, you can still spot the rainbow-angle where the curve hits a minimum.

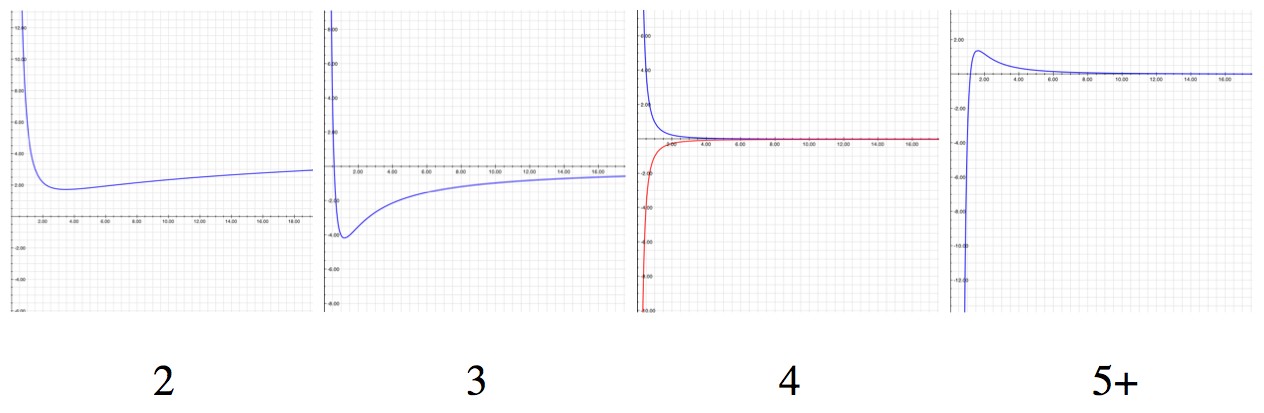
So, here’s the curve for water turning-angle, alongside the curve for diamond (which has an index of refraction of about 2.4, but that depends on color too):

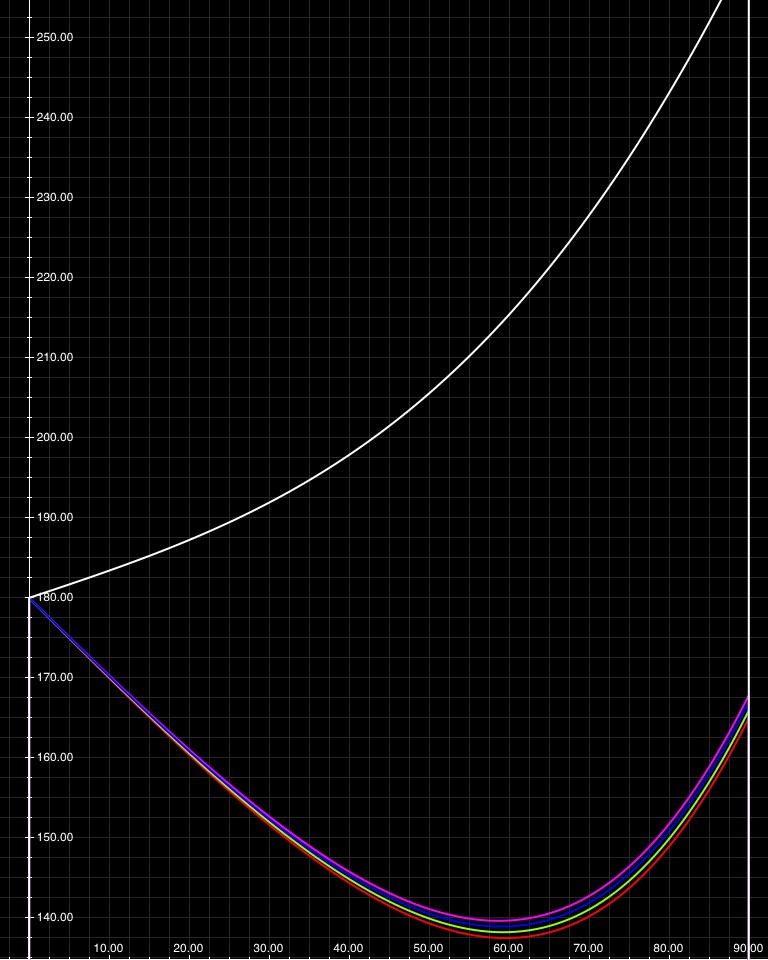
The angles that diamond droplets redirect light (white) and the angles that water redirects light. Since the diamond curve has no minimum, there's no angle where any color is strongly favored the way it is in water. For 1 reflection all of these curves will start at 180°, because light that hits the drop straight on (see top picture in this post) bounces once and comes right back out.

So: case closed.  No diamond rainbows.  But what about secondary rainbows?

You can bounce more than once inside of the droplet before coming out.  Each time a beam of light hits the side of the droplet most of the light exits but some of it is reflected back in.  One reflection gives you the standard rainbow, but two reflections gives you a second rainbow (hence: double rainbows).

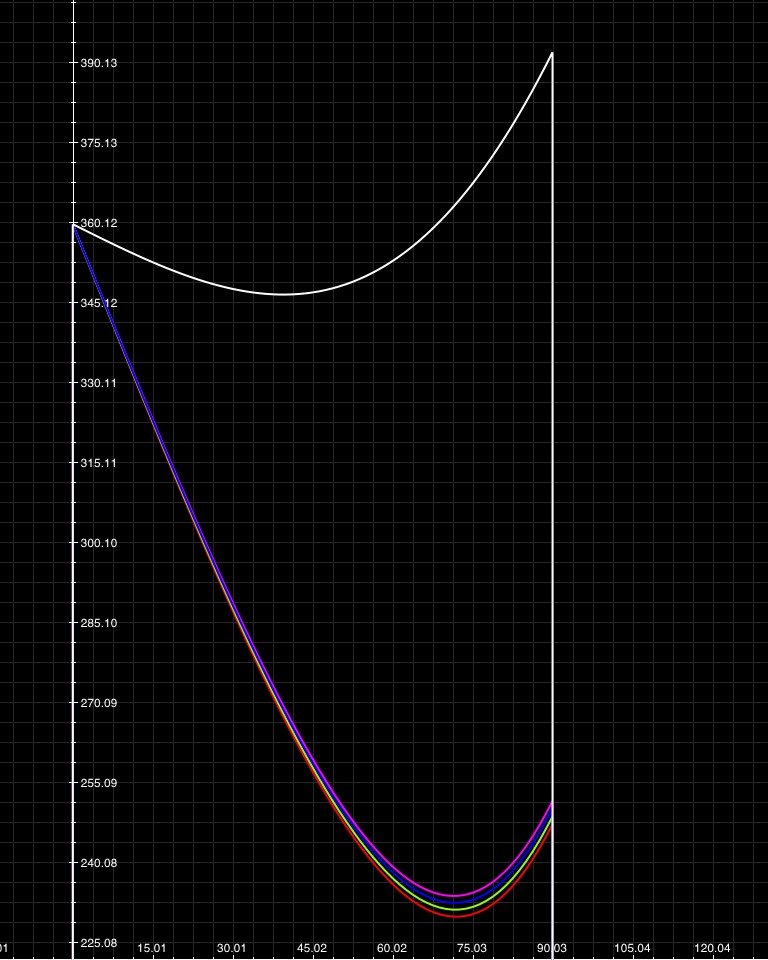
For two internal reflections you get the water-based secondary rainbow at 230° (so you'll see it in a 50° arc around the usual 40° rainbow) and the diamond-based secondary rainbow at around 350°. So the secondary diamond rainbow will be very dim (two reflections) and will be in a 10° arc around the sun. This physicist declares it ignorable.

Three reflections?  Sure!

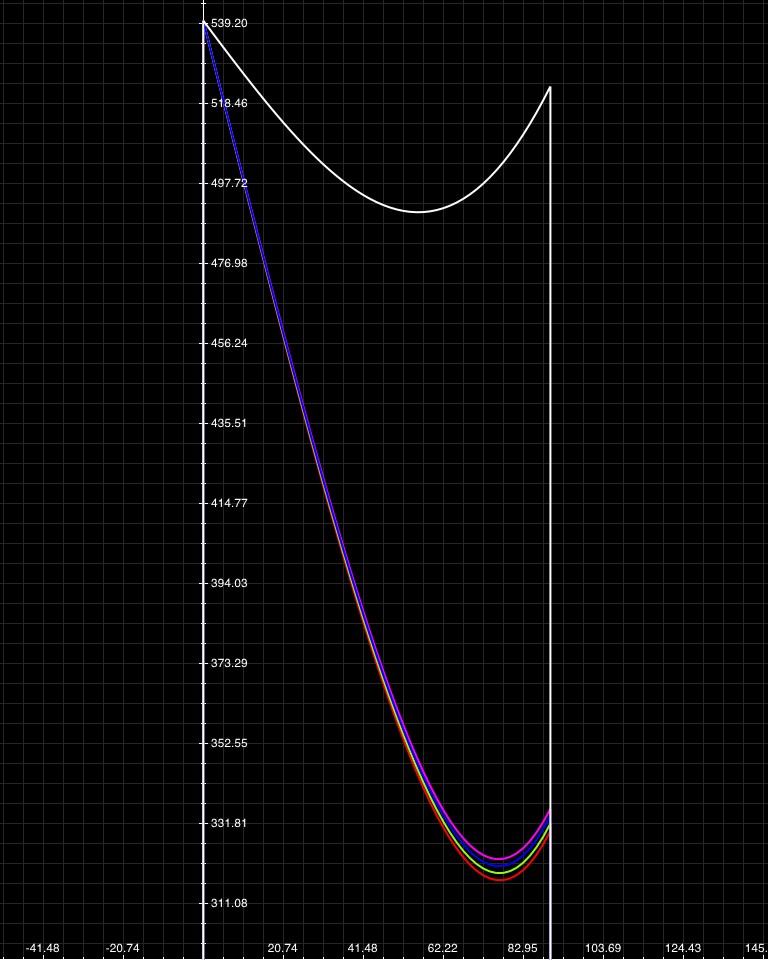
With three reflections you find that water creates a tertiary rainbow at 320° (40° around the sun), and diamond creates a tertiary rainbow at 490°, which would be a 50° arc opposite the sun.You've probably never noticed that third rainbow around the sun after a rain, because it's just too damn dim.

I got very stoked about this question.  So for all you other backyard rainbow-and-math enthusiasts who want to figure out when and where rainbows will show up in different materials, here’s a list of some indeces of refraction, and the equation:

A =180R-2\phi-(2+2R)\arcsin{\left(\frac{N_S}{N_D} \sin{(\phi)}\right)}

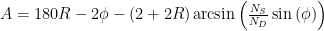
Where A is the turning angle, R is the number of reflections, ND is the index of refraction of the Droplets, and NS is the index of refraction of the Surrounding material.  \phi, again, isn’t terribly important.  Graph it, look for a minimum, and figure out what angle in the sky that corresponds too.

By the way: did you know that Titan’s atmosphere is almost all nitrogen (N=1) and that it rains liquid methane (N=1.29)?  Just saying.

I haven’t included anything about light intensity and reflection coefficients, but in general: three reflections is a bit much, and you can pretty much ignore what happens when \phi is close to 90°.

Posted in -- By the Physicist, Equations, Geometry, Physics | 4 Comments

Q: If we meet aliens, will they have the same math and physics that we do?

Posted on May 15, 2011 by The Physicist

Physicist: Similar.  We’re sure to have figured out stuff they haven’t, and they’re sure to have figured out stuff we haven’t.  But there’s likely to be a fair amount of overlap.

Some things have a way of being figured out over and over.  For example, the Pythagorean theorem got itself figured out in China, Greece, India, and Babylonia (Iraq).

Lower left: The Plimpton tablet, which lists Pythagorean triples, is from ancient Babylonia (modern-day Iraq). Upper left: a derivation of the Pythagorean theorem from ancient China (modern-day China). Right: the derivation of the Pythagorean theorem as seen in Euclid's Elements from ancient Greece.

However, there’s a fair chance that old school mathematicians were just copying each other.  Specifically, Pythagoras probably stole “his” theorem from the Egyptians (Discoveries aren’t named after the first person to make them, they’re named after the last).  Still, it’s the sort of thing that’s so useful and easy to prove that it’s hard to imagine an advanced culture not knowing about it.

And some ideas are just good.  We can say it’s very likely that aliens have invented hammers, because people (in every culture), several other varieties of apes, several monkeys species, otters (cutest), and others have all done it.  However, being a good idea doesn’t mean that different people/things will create exactly the same thing.  For example the Old World (Europe, Africa, Asia) and Incan abacuses are subtly different.

These devices, the Yupana and Abacus, which were developed independently and served the exact same function, have very different forms. (Yupana beads not shown)

Point is, there are almost certainly going to be commonalities.  At the same time, things like the Goldbach conjecture (every even number can be expressed as the sum of two primes), or half of the more obscure theorems in the more obscure mathematical disciplines, are unlikely to be in alien textbooks.  Math, being an infinite science, is going to have plenty of twists and turns that only one civilization figures out, and many more that none figure out.

Which mathematical things are most likely to be common is the sort of question best left to sci-fi writers, and other experts (such as there are).

Ultimately the physical predictions each of our sciences make will be the same.  Because of, you know: reality.  Physics is just a mathematical and philosophical structure that describes the universe.  What’s very surprising (or, alternatively, very not surprising) is that you can describe (predict) the same physical laws and behaviors based on very different (one might even say; “alien”) premises.

For example, Newton’s first and third laws (“inertia” and “for every action there’s an equal and opposite reaction”) are essentially statements about the conservation of momentum.  That is, if you total up the momentum (mass times velocity) of a closed system, then the total momentum remains constant forever.  Now, you can mumble something about Lagrangians or reference frames, but when you boil it down, conservation of momentum is just something we take as true (because it always, always works).

But an alien might have a different way of approaching the same set of laws.  Rather than saying “for a given system, if you multiply the velocity of each object with the mass of each object and add them all up you get something that never changes” (conservation of momentum), that E.T. might say something like “for a given system, the center of mass never accelerates”.  Same laws, different intuition.

Left: Normally we describe Newton's laws in terms of momentum, P = m1 v1 + m2 v2, which never changes. In this case P=0. Right: Another way to describe the same results is in terms of the center of mass never accelerating. In this case the center-of-mass' velocity is zero, and will stay that way. It turns out that, mathematically, these are interchangeable, but the philosophy is a bit different.

Like the abacus/yupana and big-rock/hammer parallels, these different theories do exactly the same thing, but look pretty different.

So (pressed for an answer), I’d expect that no matter how alien an Alien is, whether non-social, immortal, hive-minded, slug-based, whatever, their physics and math has to do a lot of the same stuff ours does, and may even be understandable (to our non-hive minds).  At the very least, our physics and Alien physics has to describe the same universe.  So, while they may have a completely different approach, it should look familiar, and ultimately do the same stuff.

Posted in -- By the Physicist, Philosophical | 12 Comments

Q: Is 0.9999… repeating really equal to 1?

Posted on May 11, 2011 by The Mathematician

Mathematician: Usually, in math, there are lots of ways of writing the same thing. For instance:

\frac{1}{4} = 0.25 = \frac{1}{\frac{1}{1/4}} = \frac{73}{292} = (\int_{0}^{\infty} \frac{\sin(x)}{\pi x} dx)^2
 
As it so happens, 0.9999… repeating is just another way of writing one. A slick way to see this is to use:

0.9999... = (9*0.9999...) / 9 = ((10-1) 0.9999...) / 9
 
= (10*0.9999... - 0.9999...) / 9
 
= (9.9999... - 0.9999...) / 9
 
= (9 + 0.9999... - 0.9999...) / 9 = 9 / 9 = 1
 

One.

Another approach, that makes it a bit clearer what is going on, is to consider limits. Let’s define:

p_{1} = 0.9
p_{2} = 0.99
p_{3} = 0.999
p_{4} = 0.9999
…
and so on.

Now, our number 0.9999... is bigger than p_{n} for every n, since our number has an infinite number of 9’s, whereas p_{n} always has a finite number, so we can write:

p_{n} < 0.9999... \le 1 for all n.

Taking 1 and subtracting all parts of the equation from it gives:

1-p_{n} > 1-0.9999... \ge 0

Then, we observe that:

1 - p_{n} = 1 - 0.99...999 = 0.00...001 = \frac{1}{10^n}
and hence

\frac{1}{10^n} > 1-0.9999... \ge 0.

But we can make the left hand side into as small a positive number as we like by making n sufficiently large. That implies that 1-0.9999… must be smaller than every positive number. At the same time though, it must also be at least as big as zero, since 0.9999… is clearly not bigger than 1. Hence, the only possibility is that

1-0.9999... = 0

and therefore that

0.9999... = 1.

What we see here is that 0.9999… is closer to 1 than any real number (since we showed that 1-0.9999… must be smaller than every positive number). This is intuitive given the infinitely repeating 9’s. But since there aren’t any numbers “between” 1 and all the real numbers less than 1, that means that 0.9999… can’t help but being exactly 1.

Update: As one commenter pointed out, I am assuming in this article certain things about 0.9999…. In particular, I am assuming that you already believe that it is a real number (or, if you like, that it has a few properties that we generally assume that numbers have). If you don’t believe this about 0.9999… or would like to see a discussion of these issues, you can check this out.

Posted in -- By the Mathematician, Equations, Math | 117 Comments

Q: What would Earth be like to us if it were a cube instead of spherical? Is this even possible?

Posted on May 9, 2011 by The Physicist

Physicist: The Earth is really round.  It’s not the roundest damn thing ever, but it’s up there.  If the Earth were the size of a basketball our mountains and valleys would be substantially smaller than the bumps on the surface of that basketball.  And there’s a good reason for that.

Rocks may seem solid, but on a planetary scale they’re squishier than soup.  A hundred mile column of stone is freaking heavy, and the unfortunate rocks at the bottom are going to break in a hurry.  Part of what keeps mountains short is erosion, but a bigger component is that the taller a mountain is the more it tends to sink under its own weight.  So as a planet gets bigger, and gets more gravity, the weight of the material begins to overwhelm the strength of that material, and the planet is pulled into a sphere.

Phobos (left), a very small moon, isn't big enough to generate the gravity necessary to crush itself into a sphere. Unlike its host planet Mars (right).

So a tiny planet could be cube shaped (it’s not likely to form that way, but whatev’s).  Something the size of the Earth, however, is doomed to be hella round.

This Cube-Earth is a lot more livable than it should be.

Life on a cubic Earth would be pretty different.  Although gravity on the surface wouldn’t generally point toward the exact center of the Earth anymore (that’ a symptom of being a sphere), it will still point roughly in toward the center.  So, the closer you are to an edge, the more gravity will make it feel as though you’re on a slope.  So, although it won’t look like it, it will feel like each of the six sides forms a bowl.  This has some very profound effects.

If you walk around the Earth's equator (left) your altitude says almost perfectly even. If you walk around the cube-Earth's equator, cutting four of the faces in half, you'd experience "altitudes" as high as 2,600km (Everest is 8.8km). The 8 corners of the cube would be 4,700km higher than the centers of each face.

The seas and atmosphere would flow to the lowest point they can find and as such would puddle in a small region in the center of each face, no more than a thousand miles or so across.  However, both the seas and atmosphere would be several times deeper.  Which doesn’t count for as much as you might think.  Here on Earth (sphere-Earth), if you’re around 5km above sea level most of the air is below you.

The vast majority of the Earth would take the form of vast, barren expanses of rock, directly exposed to space.  If you were standing on the edge of a face, and looked back toward the center, you’d be able to clearly see the round bubble of air and water extending above the flat surface.  I strongly suspect that it would be pretty.

All life (land based life anyway) would be relegated to a thin ring around the shore of those bubble seas a couple dozen miles across.

Cross-section of a face: Gravity still points roughly toward the center of the cube-Earth. As a result the water (blue) and air (light blue) flows "downhill" and accumulates at the center of each face. The only land that could be inhabited is the land surounding the sea, where the air meets the ground (green lines). This picture is way out of scale. There is no where near this much air and water on our Earth.

Assuming that the cube was oriented in the way most people are probably imagining it right now, with the poles in the center of two of the faces, then two of those bubble seas would take the form of solid ice cap blocks.

What’s really cool is that the cube-Earth would have 6 completely isolated regions.  There’s no good reason, beyond some kind of “local panspermia“, for the life on each face to be related to the life on each of the other faces.  If the biospheres took different routes  you could even have a nitrogen/oxygen atmosphere on some faces (like we have) and a hydrogen/nitrogen/carbon-dioxide atmosphere on others (like our old atmosphere 3 billion years ago).

The small area would also affect (end) large-scale air and water movement.  You wouldn’t have to worry about hurricanes, but the cube-Earth would also have a really hard time equalizing temperature.  If you’ve jumped into the Pacific Ocean on the west coast (of the United States) you’re familiar with the teeth-chattering horror of the Arctic currents, and if you’ve been in the Atlantic Ocean on the east coast (USA again) you’re no doubt familiar with the surprisingly pleasant equatorial currents.  Point is: there’s a lot of thermal energy being carried around by the air and water.  On cube-Earth you’d have to deal with huge seasonal temperature fluctuations.

If I had to guess; it’s unlikely that complex life would evolve on a cube Earth.  However!  If it did, then their space program would be as easy as a long walk, and their handsomest physicists would spend their time pondering what a round Earth would be like.

By the by, the cube earth photo is by “Altered Realities“.

Update: The dude over at Possibly Wrong went through a bunch of the math behind the gravity of cube earths, and filled in a lot of the details that this post left out.  It’s clearly presented, and well worth a look: Possibly Wrong: If the Earth Were a Cube.

Posted in -- By the Physicist, Astronomy, Physics | 85 Comments