Q: How do velocities add? If I’m riding a beam of light and I throw a ball, why doesn’t the ball go faster than light?

Posted on May 8, 2011 by The Physicist

Physicist: Everything in special relativity, no matter how weird, eventually boils down to the speed of light being the same to everyone.  It’s just not immediately obvious how.  The very short answer is: if v and w are pointing in the same direction, then their sum, V, is V = (v+w)\left(1+\frac{vw}{c^2}\right)^{-1}.

A fanatical adherence to this principle (that the speed of light is the same to everyone) allows relativistic effects to change the distance and time between events, slow the passage of (other) people’s time, even (under the right conditions) rearrange the order of events.  However, what it can’t change is that an event happens, and (oddly enough) it can’t change the ordering of speeds in any particular direction.

Say you take one direction, and you have a variety of things traveling in that direction going fast, faster, and fastest.  While different perspectives may disagree on exactly how fast each one is going, they will all agree on the same fast-faster-fastest ordering.  And light is always the same, and always the fastest.

Imagine pitching great Walter Johnson throws a baseball at 0.3c (30% of light speed, or about 200 million mph).  Clearly Walt (being stationary) is moving slower than the ball.  In turn, the ball is clearly moving slower than a passing beam of light.

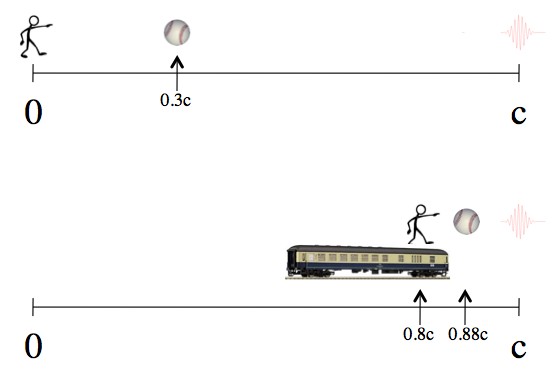
Top: for the pitcher's point of view he's sitting still (zero velocity), the ball is moving at 0.3c, and light is moving at c. Bottom: the same situation, but moving to the right at 0.8c. This is how you "add" 0.3c and 0.8c.

Now imagine that, unbeknownst to Walt, the entire baseball field was actually on some kind of super train tearing through the countryside at 0.8c.  “Intuitively”, if the usual addition of velocities held up, the ball should be traveling at 1.1c (0.8c+0.3c).  But relativity, being neither kind nor reasonable, elects instead to be stubborn about the whole “speed of light thing”.

Even on the train, Mr. Johnson is certainly still traveling to the right slower than the ball, which is still traveling slower than the light.  Moving to a different frame doesn’t change the order, it just scrunches all the velocities up.

If light obeyed the normal addition of velocities, then the speed of the light beam that pitching great Walter Johnson saw should now be 1.8c as seen by someone watching from beside the train tracks (the c Walter saw, plus the 0.8c of the train moving the whole shebang), and there should be no scrunching.  But it isn’t 1.8c!  That’s where the fact that the speed of light is the same in all reference frames comes up.

In Walter’s frame (top) the light is (naturally) traveling at light speed, and the ball is traveling slower than that.  In the frame where the whole thing is passing by on a train (bottom), the same light is still moving at c, and the ball (although traveling at a different speed) is still slower.

The classic question “what happens if I’m already on a beam of light and…” sadly doesn’t make sense from a physicsy standpoint.  No material can travel that fast.  In fact, nothing that experiences time can move that fast.  You’re always restricted by the fact that, from your own point of view, you’re sitting still and light is traveling at light speed (try it!).

If you’d like to find out why in the example above the ball ended up traveling at 0.88c instead of something else, or what would happen if Walter “The Big Train” Johnson had thrown the ball sideways off of the train, you’ll find it milling about in the answer gravy.

By the way, here’s the same example as seen from the baseball’s point of view:

On the off chance that the question would come up, and just to emphasize the symmetry of it: this is the same example from the baseball's point of view.

Answer gravy: When you go from one frame to another (changing from moving at one speed to moving at another) all you’re really doing is rearranging coordinates.  This rearrangement is called a “Lorentz boost” or a “Lorentz transformation“, and it’s surprisingly similar to a rotation (which is also just a rearrangement of coordinates).  Adding velocities amounts to applying a series of Lorentz boosts.

When doing a “coordinate transform” the weapon of choice is matrix multiplication.  It’s easy stuff.  If you can add and multiply you can do matrix multiplication.  Although I won’t lay out the technicalities here, I’ll try to be gruesomely slow algebraically.

Also, when dealing with 4-velocities (velocities that have 3 space components and one time component) it happens to be useful to not consider the time dimension, “t”, by itself, but rather “ct”.  You can think of this as natural units, or whatever.  It just tends to make everything work out beautifully.

A general 4-velocity looks like this: \left( \begin{array}{c} \frac{d(ct)}{d(c\tau)}\\\\\frac{dx}{d (c\tau)}\\\\\frac{dy}{d (c\tau)}\\\\\frac{dz}{d (c\tau)}\end{array}\right) where \tau is the on-board time of the moving thing.  This allows you to keep track of both the velocity in space (\frac{dx}{d(c\tau)}, \frac{dy}{d(c\tau)}, and \frac{dz}{d(c\tau)}) as well as time (\frac{d(ct)}{d(c\tau)}).

An object at rest has a velocity of \left( \begin{array}{c} 1\\\\0\\\\0\\\\0\end{array}\right), that is: it’s traveling through time at one second per second (one second of your time per second of on board time).

The matrix of the Lorentz transformation to a frame moving at velocity v in the x-direction is given by: \left( \begin{array}{ccccccc} \gamma && \gamma \beta&&0&&0\\\\\gamma\beta&&\gamma&&0&&0\\\\0&&0&&1&&0\\\\0&&0&&0&&1\end{array}\right), where \beta = v/c and \gamma = \frac{1}{\sqrt{1-\beta^2}}.  Gamma (as regular readers are probably sick of regularly reading) is a measure of, among other things, how much time slows down at high speeds, and is often used as a short-hand way of describing those speeds, as in “moving at a gamma of 3”.  Beta (\beta), on the other hand, is just a more reasonable way of talking about speed.  For example, when you say “half of light speed” what you’re saying is “\beta=0.5“.

Matrix aficionados may notice that this looks almost like a rotation in the time and x directions.  Just a note, those 1’s mean that the y and z components are unaffected.

So when the pitcher throws the stationary ball he “boosts” it into a new frame (by making it move).  Mathematically you can do this with matrix multiplication:

\left( \begin{array}{ccccccc} \gamma && \gamma \beta&&0&&0\\\\\gamma\beta&&\gamma&&0&&0\\\\0&&0&&1&&0\\\\0&&0&&0&&1\end{array}\right) \left( \begin{array}{c} 1\\\\0\\\\0\\\\0\end{array}\right) = \left( \begin{array}{c} \gamma\cdot 1+\gamma\beta\cdot 0+0\cdot 0 +0\cdot 0\\\\\gamma\beta\cdot 1+\gamma\cdot 0+0\cdot 0 +0\cdot 0\\\\0\cdot 1+0\cdot 0+1\cdot 0+0\cdot 0\\\\0\cdot 1+0\cdot 0+0\cdot 0+1\cdot 0\end{array}\right) = \left( \begin{array}{c} \gamma\\\\\gamma\beta\\\\0\\\\0\end{array}\right)

The top \gamma is time dilation.  \frac{d(ct)}{d(c\tau)} = \frac{dt}{d\tau} = \gamma means that for every second that passes for the baseball (\tau) \gamma seconds pass for you.  Also, you can get rid of the on-board time dependence and recover “normal” velocity (dx/dt, no “\tau‘s”) with a little algebra.  Normal velocity (in the x-direction) is: \frac{dx}{dt} = c\frac{dx}{d(ct)} = c\frac{dx}{d(c\tau)}\frac{d(c\tau)}{d(ct)} = c\left( \gamma\beta \right) \left(\frac{1}{\gamma} \right) = c\beta = c\left(\frac{v}{c}\right) = v.

So, the baseball is moving with ordinary velocity v (like you’d hope) and 4-velocity (\gamma, \gamma\beta, 0,0).  To see what happens when we boost again, by moving to a new frame where the ball’s velocity is being added to the velocity of the train, just do another matrix multiply.  This time with: \left( \begin{array}{ccccccc} \Gamma && \Gamma \alpha&&0&&0\\\\\Gamma\alpha&&\Gamma&&0&&0\\\\0&&0&&1&&0\\\\0&&0&&0&&1\end{array}\right)  It’s the same thing, just with a different speed from last time.  This time \alpha = w/c, and \Gamma=\frac{1}{\sqrt{1-\alpha^2}}.

\left( \begin{array}{ccccccc} \Gamma && \Gamma \alpha&&0&&0\\\\\Gamma\alpha&&\Gamma&&0&&0\\\\0&&0&&1&&0\\\\0&&0&&0&&1\end{array}\right) \left( \begin{array}{c} \gamma\\\\\gamma\beta\\\\0\\\\0\end{array}\right) =\left( \begin{array}{c} \Gamma\cdot \gamma+\Gamma\alpha\cdot \gamma\beta+0\cdot 0 +0\cdot 0\\\\\Gamma\alpha\cdot \gamma+\Gamma\cdot \gamma\beta+0\cdot 0 +0\cdot 0\\\\0\cdot 1+0\cdot 0+1\cdot 0+0\cdot 0\\\\0\cdot 1+0\cdot 0+0\cdot 0+1\cdot 0\end{array}\right) =\left( \begin{array}{c} \Gamma\gamma(1+\alpha\beta)\\\\\Gamma\gamma (\alpha+\beta)\\\\0\\\\0\end{array}\right)

So, what’s the normal velocity after adding the speeds v and w?  What is the final velocity “V”?  Algebra!:

\begin{array}{ll} V = \frac{dx}{dt}\\= c\frac{dx}{d(ct)}\\= c\frac{dx}{d(c\tau)}\frac{d(c\tau)}{d(ct)}\\= c\Gamma\gamma (\alpha+\beta)\left(\frac{1}{\Gamma\gamma(1+\alpha\beta)}\right)\\= c\frac{\Gamma\gamma (\alpha+\beta)}{\Gamma\gamma(1+\alpha\beta)}\\= c\frac{\alpha+\beta}{1+\alpha\beta}\\= c\frac{w/c+v/c}{1+(w/c)(v/c)}\\= \frac{w+v}{1+(w/c)(v/c)}\\= \frac{w+v}{1+\frac{wv}{c^2}}\end{array}

Holy crap!  The equation we normally think is right, V = v+w, doesn’t work.  But stir in a little special relativity and you get: V=(v+w)\left(1+\frac{vw}{c^2}\right)^{-1}.

So, in the example from (way) above the speeds were v=0.3c and w=0.8c.  So V=\frac{0.3c+0.8c}{1+(0.3)(0.8)} \approx 0.887097c

Seems like a long trip for \left(1+\frac{vw}{c^2}\right)^{-1}, but there it is.  This little term keeps the speed of light in the right place, and adjusts every other velocity to stay in the right place.  At low (compared to light) speeds vw is overwhelmed by c2 and 1+\frac{vw}{c^2} is very close to 1.  In other words, when you’re not cruising about at crazy speeds you get the usual rules.

Finally, if you choose to add velocities that aren’t in the same direction, you just have to rotate one of the Lorentz matrices.  For example, while all of the examples so far have been in the x direction, a boost in the y direction would be given by: \left( \begin{array}{ccccccc} \gamma && 0&&\gamma \beta&&0\\\\0&&1&&0&&0\\\\\gamma\beta&&0&&\gamma&&0\\\\0&&0&&0&&1\end{array}\right)

If Walter Johnson had decided to throw the ball in the y direction on the train, and everything else stayed the same, you’d figure out the end 4-velocity of the ball by doing the following boosts:

\left( \begin{array}{ccccccc} \Gamma && \Gamma \alpha&&0&&0\\\\\Gamma\alpha&&\Gamma&&0&&0\\\\0&&0&&1&&0\\\\0&&0&&0&&1\end{array}\right) \left( \begin{array}{ccccccc} \gamma && 0&&\gamma \beta&&0\\\\0&&1&&0&&0\\\\\gamma\beta&&0&&\gamma&&0\\\\0&&0&&0&&1\end{array}\right) \left( \begin{array}{c} 1\\\\0\\\\0\\\\0\end{array}\right)= \left( \begin{array}{ccccccc} \Gamma && \Gamma \alpha&&0&&0\\\\\Gamma\alpha&&\Gamma&&0&&0\\\\0&&0&&1&&0\\\\0&&0&&0&&1\end{array}\right) \left( \begin{array}{c} \gamma\\\\0\\\\\gamma\beta\\\\0\end{array}\right) =\left( \begin{array}{c} \Gamma\gamma\\\\\Gamma\gamma\alpha\\\\\gamma\beta\\\\0\end{array}\right)

It seems a little spooky that when the velocities aren’t parallel, velocity addition is no longer commutative (notice that the alphas and betas aren’t on equal footing), and the order in which you do the boosts becomes important.  Of course, it may be spooky that that isn’t always the case.

Posted in -- By the Physicist, Physics, Relativity | 23 Comments

Q: What is the universe expanding into? What’s outside the universe?

Posted on May 5, 2011 by The Physicist

Physicist: Probably nothing.  We do know that the universe doesn’t need anything to expand into, and we haven’t seen any evidence that there is anything outside of the universe.  But there has still been some speculation.

In the last hundred years physics has gotten pretty weird, and defining “universe” has become a little tricky.  So, in what follows I’m defining the universe as “all the places that could be connected to one another by a sufficiently long rope” (never mind how the rope got there).

Having never been outside of the universe, it’s hard to discuss it with any certainty.  Most of the theories about the outside of the universe fall into the “I can’t say you’re wrong for sure” category.

We can say that space isn’t “made of anything”, and that it doesn’t need any kind of “higher space” to exist in.  If space did need some other kind of space to live in, you find that the question just gets pushed back.  After all, what’s outside of that space?

In a conversation about spacetime often as not you’ll have some unpleasant and unrepentant jackass drawing parallels to rubber or sheets or something else material.  It’s not that these metaphors are misleading (although they are a little) it’s that they reinforce the quiet, underlying assumption that space is made of something, and that it needs somewhere to be.  About the best definition of space is “Space is nothing more and nothing less than what rulers measure”.  If you think about some of the properties of space, as described in relativity (both general and special), you find that it has all kinds of properties that a material can’t have.

For example, there’s no difference whatsoever between moving and being stationary.  So, it’s impossible to meaningfully talk about “moving through space”, when you may as well be motionless.  Even worse, you can fit an arbitrarily large amount of space within any volume (as measured from outside that volume).  Think: Dr. Who’s TARDIS.  Or, if that’s not your thing: the diameter of a circle drawn around the volume can be arbitrarily great, while the circumference stays finite.

Point is: space isn’t stuff.  And the universe doesn’t need anything to expand into.

When you picture the universe as a whole it’s almost impossible not to think of a fish bowl or a bubble.

The Universe: Nothing like this.

Implicit in that picture of the universe is an outside.  However, that outside is defined in terms of space, and all of space should be inside the universe.  When you try to talk about the outside of the universe you find yourself asking questions like “okay, where are you?” or “how far from the universe are you?”, you know, the types of questions that really rely on some notion of position and space.

That all being said, there are some theories that do talk about things outside of the universe.  There are some proponents of M-theory who claim that the universe could be a sheet floating in a higher dimensional space, and that there are other universe-sheets floating along side us, just a tiny distance away.  Although the other sheets act exactly like what almost everybody would call “other universes”, it’s would be slightly more accurate to say that the collection of sheets and the higher space they float around in are all part of the same “super-universe”.  They’re still at least a little connected to each other.

Aside: Btw, when physicists want to talk about more than three dimensions they (being born and bred here) like to knock off dimensions to help picture things.  So, if you want to imagine the universe in a higher dimensional space, just get rid of a dimension.  The universe goes from a 3-D volume to a 2-D “sheet”.

The universe may also have “bubbled off” of some other larger universe, or spontaneously started, or who knows.  If there are truly other universes, or any other stuff outside of our universe, it’ll be “causally separated” from everything going on here (or that has or ever will go on here).  Rather than thinking of other universes as being “somewhere else” it’s better to think of them as “in every way independent”.  You can’t even sensibly talk about “going there”.

Science (and more generally: everything we can know), being based on observation, inference, and experience, can’t say much about things entirely outside of the universe.  We can infer, and make some spectacular guesses, but that’s about all.  In another 20 years or so our entire approach to the nature of the universe will have completely changed (it always seems too).

Posted in -- By the Physicist, Astronomy, Philosophical, Physics | 63 Comments

Cheap experiments and demonstrations for kids.

Posted on May 2, 2011 by The Physicist

The original question was: I recently had to cover teaching children (Age 10 – 14) physics for an hour and I was wondering if you could think of any physics experiments that require few or cheap materials with interesting results that we could use to springboard onto other topics?

Physicist:

Dry ice.

Dry ice is pretty cheap and there are all kinds of uses for it:

-In a pitcher it creates enough cold air and mist that you can literally pour the air onto a table top, and demonstrate how temperature differences give rise to wind.
-You can put it in film canisters (if you can even still find them).  As it heats up it expands (technically: “sublimates”) and in a minute or so the canister will fly through the air.  Nice pop.  Grabs attention.  You can use this to talk about the ideal gas law.
-Fill a fish tank or other large glass container with about half an inch of water and put a fist of dry ice in it.  It releases enough cold air and CO2 (which is heavier than air) that you can then float stuff on it, like balloons or bubbles.  In case you’re wondering, there’s enough thermal noise and air movement to keep the gases in our atmosphere from stratifying (which is why we have a mix of gases including oxygen down here, instead of drowning in argon).

What ever you do, don’t cover the top of the tank.  Also, high concentrations of CO2 are a bit corrosive, so don’t go breathing the air in the tank directly.  If you must: waft.

This image stolen from: http://www.wired.com/wiredscience/2007/12/lecture-videos/

The pendulum trick gets people up and moving, and I find that middle school kids are perfectly happy to try it:

-Get something heavy/dangerous like a bowling ball or a can full of rocks/sand and string it to ceiling.  Pull it way back, hold it to your nose, and let it go.  As it swings away the gravitational potential energy from being elevated (be careful not to say “being high”, 14 year olds never miss that) turns into kinetic energy and back.  By conservation of energy it can’t swing any higher than it started, so it will come up to within an inch or so of your face.

To help hold the person’s face in place it helps to have something to put your chin on.
I’ve seen people accidentally lean forward and get slammed.  You have to lean back a little to hold the pendulum, so usually it’s best to have someone else hold the pendulum, while the “victim” stands perfectly still.  Also, it’s important to avoid the instinct to give it a little push (it was hilarious at the time, but only because nobody was really hurt).

Pulleys!

With a couple pulleys and some rope you can have a tug-of-war between completely imbalanced teams.  Then you can talk about leverage, force, and work.  As in, “work equals force times distance” so even though one team pulled with less force, they covered a greater distance and so did the same amount of work.

A diffraction grating being used for some terrifying clandestine purpose.

If you have some time you can also get some “linear diffraction gratings” for practically nothing.  They’re basically very light weight prisms, but work much better, and with them you can talk about atomic spectra.  Some things to look at: florescent lights, LEDs, any kind of neon light, street lights, …

I used one to get the right half of the middle picture from this post.  In practice the image you see is a lot clearer than that picture implies (Cell phone cameras were not made for this sort of thing).

Also, since they’re essentially just a series of extremely small slits, they work on the same principle as the “double slit experiment”, just with more slits.  So for example if you shine a laser though a diffraction grating it will split into several beams because of interference.

The standard park merry-go-round. In German: das pükmacher.

If you have access to a merry-go-round you can talk about the coriolis effect, and make some kids throw up (that’s a twofer).  If the merry go round has a smooth surface, all the better.  If not you can attach a plywood sheet on top of the merry-go-round to make a spinning table.

Have the kids gather around the table, on the merry-go-round (while spinning), and try to roll the marble back and forth.  The kids on the merry-go-round will see the marble suddenly swerve to the side as it crosses the table, while all the kids standing around (waiting their turn) will see the marble travel in a (roughly) straight line.  The difference between the rotating frame where things swerve, and the stationary frame where they obey the usual physical laws, is ultimately what’s responsible for things like hurricanes.

If you don’t have something to roll a marble across you can just have them throw bean bags, or any other soft thing, back and forth while standing on the merry-go-round.  The soft is important because they’ll miss a lot at first.  Sometimes I’ll find someone who gets so used to the coriolis forces (and has a strong stomach) that they can throw the bean bag into the air in such a way that it loops and comes back to them.  Of course, everyone standing on the sides sees that they’ve just managed to time the throw so that it gets to the far side of the merry-go-round at the same time the person does.
It may help to make this into a game.  Being outside makes kids crazy.

Van der Graaf generator

There’s a lot you can do with electricity on the cheap, but half of it is dangerous (in the wrong hands), and half of it is almost exclusively found in physics departments.  If you can get your hands on a Van der Graaf  generator, whoever you borrow it from will have some suggestions.  My favorite is throwing packing foam (“ghost poo”) at the generator, or just putting a bowl full of packing foam on top of the generator.

The whole experiment. This image stolen from: http://hubpages.com/hub/Homeschool-Science-Curriculum–Magic-Bending-Water

You can also comb your (clean) hair with a (clean) comb to build up a charge on the comb.  Get a stream of water as thin as you can before it breaks up into individual drops, and bring the comb next to it.  The water will polarize (the positive side of each molecule will point toward the comb… or the negative side, I forget) and the stream will bend toward the comb.

The geometry of pin hole cameras.

Pin hole cameras.  You can talk about images on the back of the eye being flipped by drawing the set up on a chalkboard and going through which paths the light has to take as in: “traveling in a straight line through the hole, where is the image of this part going to be?”.  Or, if you can adjust how wide the aperture is, you can show how squinting works.

Micrometeorites are about the size of individual grains of fine sand, but they fell from space, so it still counts.

If you have access to a lot of microscopes and magnets, you can find micro-meteorites.
1) Cover a strong magnet with a plastic bag or saran wrap.
2) Find some open dirt and wave the magnet just barely above the ground so that (if you listen closely) you’ll hear a clicking as tiny particles fly into the magnet.
3) After a while, take off the plastic and put the dirt on a slide.
4) Under a microscope (with the help of a tooth pick) you can find and isolate tiny iron spheres.  These are the micro-meteorites.

When a meteor (big or small) is burning up in the atmosphere, if it’s metallic, it will shed tiny pieces of molten metal.  These rain down evenly over the entire planet, and are common enough that in any pinch of dust you can usually find one or two.
They appear as unusually round metal balls, and are surprisingly small.  So try this yourself before making kids do it (a little practice goes a long way).

Safety notes: As for dry ice; don’t put the dry ice in anything more secure (or that could potentially be more secure) than a film canister.  Ever, ever, ever, holy crap, ever.  Depending on the container, the explosion can do a surprising amount of damage.  Also, if any kid gets a hold of dry ice and does something like put it in their mouth, the best thing you can do is slap it right out of their face.

Alternatively, let them keep it.  None of the other kids will want to try it afterward.

As for Van der Graaf generators: home made generators can be more dangerous than store bought generators, because most companies have acute liticaphobia.  As a general rule, keep old people and anyone with a heart condition away from high voltage.  Unless it’s huge, a Van der Graaf generator won’t kill you, but it will hurt like a sonofabitch.  Getting tagged by one is the sort of experience that really sticks with you.  Keep a physicist or electrical engineer on hand.

Disclaimer: All of the above suggestions are believed to be safe, but perform them at your own risk. Safety precautions are advised!

Posted in -- By the Physicist, Experiments, Physics | 8 Comments

Q: How do I estimate the probability that God exists?

Posted on May 1, 2011 by The Mathematician

Mathematician: Before jumping into this question, it is important to realize that probabilities are not objective, observer independent quantities. We can think of the claim that a particular outcome will happen with a probability of 0.30 as meaning (loosely speaking) that given the information available to me right now, if I could replay this scenario many times, then in about 30% of those occurrences I would expect that particular outcome would occur. Notice that this means that my estimated probability may change if the information that I have changes.

To illustrate this concept, consider what happens when different people have different information about the nature of a single coin. For instance, suppose that I flip a coin, and you have to guess whether the coin lands on heads or tails. From your perspective, you estimate that the probability of a head occurring is 50%, based on what you know about coins in general, and the fact that you have no knowledge indicating that a head would be either more or less likely to occur than a tail for this coin. I, on the other hand, am aware that this is a trick coin with a head on both sides. So from my perspective, the coin has a 100% chance of landing on heads. Little do I know, however, that the coin is in fact a magic coin (the warlock who sold it to me at the carnival forgot to mention this fact) — 30% of the time this two-headed coin is flipped it magically changes into a two-tailed coin before landing. Hence, from the warlock’s perspective, the probability that the coin will end up showing heads is 0.70, whereas from my perspective the probability is 1.0, and from your perspective it is 0.50.

So getting back to the God question, we cannot talk about a single, universal probability that God exists. Rather, this probability will necessarily be dependent on the information that you happen to have.

Another important observation is that it is problematic to throw around the word God relying on the assumption that we all know what that means. How are we going to define God? If it turns out that Zeus exists, would we consider that God? What if our universe was created by a pair of powerful, omniscient, omnibenevolent beings? Would we consider them both God? Or how about if our universe was created by an alien scientist, would we consider that scientist God?

We cannot possibly assign a probability to “God” without specifying further what is meant by this term. Hence, rather than a single God probability, it is more reasonable to consider the probability that each possible god G exists (using whatever definitions for G we care to analyze). This information can be encapsulated by a function P. For each event Gexists, representing the existence of god G, P(Gexists) gives the probability of that event (i.e. the probability that G exists). As we have seen, the function P will depend on all the information that you currently have, which we will call your evidence E. Therefore, it is more rigorous to write this function as P(Gexists|E). This is what’s known as a “conditional probability”, and the vertical bar “|” is typically read as “given”. Hence, P(Gexists|E) can be thought of as “the probability that god G exists given our evidence E.”

Estimating the function P(Gexists|E), which assigns probabilities to the existence of possible gods G, is no trivial matter. For one thing, the human brain misjudges probabilities all the time (See this, that, this other thing and also this for some standard examples). Despite these challenges, we can talk about some useful rules that should be taken into account during this process of estimating P(Gexists|E):

  1. If the evidence E that we have is really unlikely to have occurred given the existence of a particular god G (but not so improbable otherwise), then that will tend to make the god G less likely. An extreme example of this is that if G is defined to be “an all powerful god that would never allow human beings to live”, then because our evidence E includes living human beings, that god G can’t exist (so we’ve just disproved a god!). Another example is that if your evidence says that there is a lot of evil in the world, then that is going to make any very powerful god that wouldn’t allow evil pretty unlikely.
  2. The more conditions we tack onto our definition of a god G, the less likely it will necessarily be that the god G exists. For example, a god that “is omnipotent and omnipresent” is going to be strictly less likely than a god that is just defined to be “omnipotent” or just defined to be “omnipresent”, since the probability that two conditions are met is always less than or equal to the probability that just one of those conditions is met (and neither omnipotent nor omnipresent implies the other, making this inequality strict). Similarly, a god that “helped the Jews escape from Pharaoh” is going to be more probable than a god that “helped the Jews escape from Pharaoh by parting the sea”, since the latter is the same as the former except with extra conditions. And this is not a statement of opinion, but rather, a consequence of the rules of probability.
  3. Make sure that the way you use probabilities conforms to Bayes’ Rule. This mathematical rule tells us that something is evidence in favor of a particular hypothesis if that something is more likely if that hypothesis is true than if the hypothesis is false. So, for example, the fact that canaries exist is (a small amount of) evidence in favor of a creator god that loves canary-like-things (compared to the hypothesis of a creator god that doesn’t love canary-like-things) since the probability of canaries existing is greater if a creator god loves canary-like-things than if a creator god does not.
P(“God of two giant hands in the sky exists”) < P(“God of at least one giant hand in the sky exists”)

 

These rules aside, giving advice about how to estimate P(Gexists|E) is quite difficult. But, I can at least warn you away from a few very common but very flawed methods for estimating the probability of various gods.

Bad Method 1:

Set P(Gexists|E) = 1  for whichever god you were taught about as a child, and setP(Gexists|E) = 0 for all other gods. This strategy works well on average only if  (a) there really is a god and (b) that god is by far the most popular god. Given, however, that there is no religion which more than one third of the people in the world believe in (not to mention the huge amount of disagreement within each individual religion about the exact nature of god), this strategy will assign 100% probability to an actually existent god less than one third of the time, regardless of what the truth about god actually is. (At least, this is true as long as we consider the Muslim Allah to be a different god than the Christian one, and both of them to be different than Vishnu, etc.). In fact, the odds could be much worse, if it turned out that, say, only 3,000 people in the world have identified the one true religion (which implies that you almost certainly weren’t raised in that religion as a child, and hence that your function P(Gexists|E) will almost certainly assign 100% probability to the wrong god if you use this bad method).

Bad Method 2:

Use a definition of god that is vague enough that you yourself don’t have much of a clue what “god” really means (e.g. “god is a force” or “god is that which is good”), and then assign P(Gexists|E)=1 for this vague god and P(Gexists|E)=0 to, well, whatever is not covered by this definition. Definitions like these are just too fuzzy to mean very much. If you try to apply reasoning to fuzzy, ill-defined ideas, you’ll often get nonsense as a result. Case in point, lame attempts such as: “God is good” and “Good exists”, therefore “God exists.”

Bad Method 3:

Assign a high probability to things that appeal to you, and a low probability to things that do not appeal to you. Hopefully the problems with this approach are fairly obvious. You may have had a happy day dream about a guardian angel that is looking after you, you may desperately want there to be such an angel, you may spend hours thinking about such angels, but none of that constitutes useful evidence about whether an angel will actually catch you if you trip and fall down the stairs. You cannot (rationally) believe something simply because you want it to be true. You can only (self-delusionally) believe something because you want it to be true.

Bad Method 4:

Only seek out information that supports your pre-existing beliefs, and ignore or avoid information that might disconfirm your beliefs. In practice, this often amounts to starting with a high probability assigned to one particular god J that you happen to have been taught about, and starting with a low value assigned to P(Gexists|E) for other gods G. You then proceed to only ever read supportive literature (and talk to supportive people) arguing in favor of the god that you already think is likely, ignoring literature and people that discuss why god J might not exist. Of course, this approach naturally will cause you to keep increasing your probability P(Jexists|E) and keep decreasing P(Gexists|E) for the other gods, because you keep inundating yourself exclusively with information that supports what you already believed.

Imagine that someone alive in Greece in the 5th century BC were to follow this method. For instance, suppose that this person started out with only a moderately strong belief that Zeus exists, but then only ever listened to people talking about reasons why he should believe in Zeus. Because of this, his moderate belief in Zeus naturally would have risen over time until it became a strong belief. But this procedure would cause his belief in Zeus to rise whether or not Zeus exists! Hence, it is not a procedure that produces truth, it is merely a procedure that produces belief. This mistake is very common because people tend to surround themselves mostly with people who believe similar things to what they themselves believe, and members of religious communities work to convince each other to believe ever more strongly. For instance, our Greek friend would have been likely to spend most of his time around others that believed in Zeus, rather than those that were marking arguments against Zeus or in favor of a different set of gods.

In summary, to maximize your chance of believing the truth, you must not assume that what you were taught is necessarily true, you must define your terms as precisely as you can, you must surround yourself with the best possible arguments both for and against a particular belief, and you must evaluate these arguments objectively, without regard for what you want to be true.

You may at this stage be wondering: “How does the religious concept of faith factor into our probabilistic argument?” Well, the tricky part about faith is that, while it’s all very well and good to have faith in a benevolent god who does exist, it’s not a wise idea to have faith in a god who doesn’t exist. (I hope that most of us can agree on that point.) Therefore, one must choose carefully, considering the many mutually exclusive gods out there who are allegedly demanding our faith. Faith doesn’t really get us out of the probabilistic quandary of estimated P(Gexists|E). At best it just changes the probabilistic question from “which god should I believe in?” to “which god should I have faith in?” which doesn’t really help.

Probability theory provides a useful framework for thinking about God, not so much because of the specific nature of the God question, but because probability provides a useful framework that can be applied to nearly all questions of (non-tautological) truth.

 

Posted in -- By the Mathematician, Philosophical, Probability, Skepticism | 36 Comments

Q: How do you calculate 6/2(1+2) or 48/2(9+3)? What’s the deal with this orders of operation business?

Posted on April 29, 2011 by The Mathematician

Mathematician: Now that the Physicist and I have answered questions like these ones at least 9 times via email, I figure we should get this horrible topic out of the way once and for all with a short post.

The “order of operations” tells us the sequence in which we should carry out mathematical operations. It is merely a matter of convention (not a matter of right or wrong), giving us a standardized way to decide whether 6/2*3 is (6/2)*3 or 6/(2*3). The convention has been accepted just so that when different people see an equation they can agree on its meaning, even if they hate each other’s guts. You could come up with a different convention, but why bother? Let other people waste their time coming up with arbitrary conventions so that you can merely waste time reading posts about them.

The rules to follow are:

1. Things in parenthesis get computed before things not in parenthesis (this is because of the (little known fact) that parentheses kick ass).

2. Then, exponents get dealt with (including roots). Hence a^b*c = (a^b)*c.

3. Next, multiplication and division get carried out from left to right. So a*b/c*d is ((a*b)/c)*d. Note that division can be thought of as still carrying out a multiplication since a/b = a*(1/b), so it makes a certain sense that neither division nor multiplication takes precedence over one another.

4. Finally, additions and subtractions get carried out from left to right. Subtraction can be thought of as being like addition since a – b = a + (-b) so it makes sense that subtraction is treated on an equal footing with addition.

People sometimes use the expressions PEMDAS, “Please Excuse My Dear Aunt Sally” or “Puke Exhaust Mud Dolls Autumn Sasquatch” to remember these rules. These all stand for “Parenthesis, Exponents, Multiplication and Division, Addition and Subtraction”. It is easy to get confused by these mnemonics though because they don’t capture the fact that multiplication is treated the same way as division (carried out left to right), and addition is treated the same way as subtraction (carried out left to right). That’s why I prefer: “Puke Exhaust Mud And Dolls Autumn And Sasquatch”

One interesting thing to note about the order of operations is that there is nothing interesting about them whatsoever. But that implies there is something interesting about them. This is a contradiction, and hence the order of operations form a paradox. They are also about as fun as getting to watch a fish crawl up the stairs as a reward for answering math questions.

But, that won’t stop me from giving an example. Consider:

a^b*c/d+e-f.

Without a convention, it has many possible interpretations, such as

a^(b*(c/(d+e)))-f

or

(a^b)*((c/(d+e))-f)

which could be horribly confusing for people trying to communicate with each other. But, the correct interpretation according to the rules mentioned above, is:

(((((a^b)*c)/d)+e)-f).

When in doubt about what the orders of operation are for an expression, there is a simple solution which works even better than tattooing PEMDAS to your face. Just paste the expression into the google search bar and hit “search”. For instance, if I paste in:

4^2*3/6+1-5

it gives back

(((4^2) * 3) / 6) + 1 – 5 = 4. 

Not only is this the correct answer, but it shows you explicitely the order of operations that were used, so it’s useful for learning.

Google even gets this one right:

4^2*3/6 + 1 – 5/14*3 + 6/10 – 4*2/14*6^3/18 + 14

which is the kind of question little sisters give you when they are old enough to finally sort of get what a mathematician is.

It’s important to note that not all calculators handle the order of operations in the standard way. Why? Because people who make calculators hate children. The preceding sentence was not intended to be a factual statement.

Also, a lot of programming languages use the standard order of operation rules, but then you have exceptions like Smalltalk.

Oh, and in case you were wondering:

a^b^c  = a^{b^c}.

Posted in -- By the Mathematician, Conventions, Math | 342 Comments

Q: Is there a single equation that proves black holes are real?

Posted on April 25, 2011 by The Physicist

Physicist: Nope!

Using general relativity (which has plenty of equations), and a little borrowed knowledge from other fields (to describe star collapse), you can show that black holes should exist.  But unfortunately there are no proofs in physics, just experimental and observational evidence.

That being said, the observational evidence of the existence of the black holes has been extremely good.  For example, by looking at the movement of the stars in the galactic core we’ve determined that they must be orbiting a tiny, invisible object with several million Suns worth of mass.

Which sounds like pretty good evidence for a black hole!  Of course, at the end of every theory, proposition, and paper is a tiny invisible asterisk that reads:

“*All of the above assumes that something we’ve never heard of and/or could never have imagined isn’t what’s actually going on.  That would hella suck.”

From time to time “something we’ve never heard of” is exactly what’s going on, but there isn’t a lot that can be done about that.  Dismissing a working theory because something might be wrong is paralyzing.

So Sagittarius A* (the super-massive object in the center of our galaxy) is almost definitely a black hole, but it hasn’t been (and never will be completely, absolutely, and totally) proven that black holes exist.  I’m convinced though.

Posted in -- By the Physicist, Astronomy, Philosophical, Physics | 11 Comments