Physicist: When you have two finite sets it’s easy to say which one has more things in it. You count up the number of things in each, compare the numbers, and which ever is more… is more. However, with an infinite set you can’t do that. Firstly, you’ll never be done counting, and secondly, infinity isn’t a number.
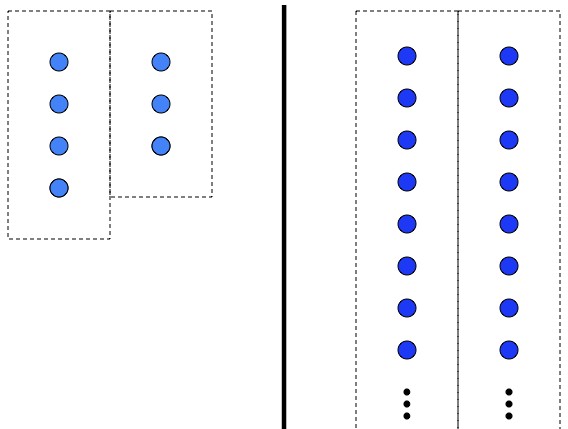
With finite sets you just compare the number of elements in each set (left), but with infinite sets that’s not an option (right). Phrases like “number of elements in the set” don’t apply.
So now you need to come up with a more rigorous definition of “same size”, that reduces to “same number of elements” in the finite case, but continues to work in the infinite case.
Here it is: instead of counting up the number of elements, and facing the possibility that you’d never finish, take the elements from each set one at a time and pair them up. If you can pair up every element from one set with with every element from another set, without doubling up and without leaving anything out, then the sets must be the same size.
Mathematicians, who enjoy sounding smart as much or more than they enjoy being smart, would call this “establishing a bijective mapping between sets”.
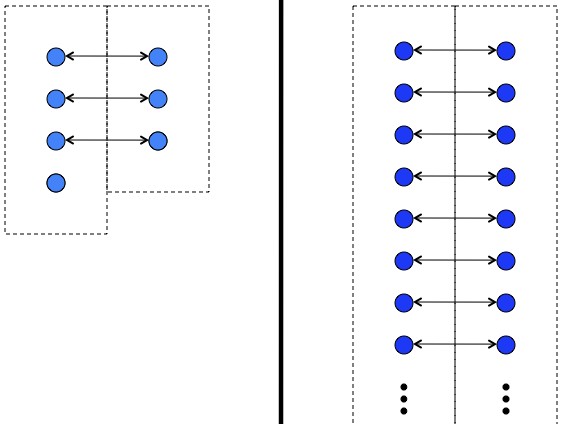
By pairing up elements you can establish that the sets have the same number of elements. The sets on the left have an unequal number of elements, and the sets on the right (somewhat surprisingly) have the same “number” of elements.
So the requirement for two sets to have the same size is that some pairing exists. For example, in the right side of the picture above you could have chosen to pair up every element in the left column with the element below and to the right forever, leaving the one element
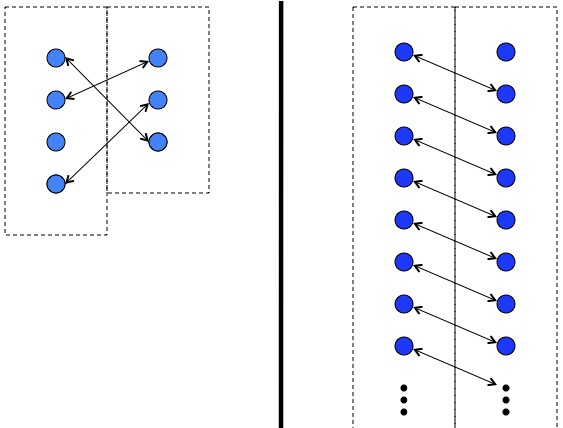
If you rearrange the pairing for finite sets you’ll find it has no effect: there will be the same number of unpaired elements. Infinite sets are not so restricted. Literally, ∞ +1 = ∞.
Even worse, you can show that two sets that have “obviously” different sizes are in reality the same size. For example, the counting numbers (1, 2, 3, …) and the integers (…, -2 , -1, 0, 1, 2, 3, …):

One of the classic “thought experiments” of logic is similar to this: You’re the proprietor of a completely booked up hotel with infinite rooms. Suddenly an infinite tour bus with infinite tourists rolls up. What do you do? What… do you do?

The first vanguard of a never waning flood of tourists.
Easy! Ask everyone in your hotel to double their room number, and move to that room (where there should be a gratis cheese basket with a note that says “sorry you had to move what was most likely an infinite distance“). So now you’ve gone from having all of the rooms full to having only all of the even rooms full, while all of the odd rooms are vacant.
Another way to look at this is: ∞ + ∞ = ∞.
Here’s something even worse. There are an infinite number of primes, and you can pair them up with the counting numbers:

There are also an infinite number of rational numbers, and you can pair them up with the counting numbers.

Arrange the rational numbers in a grid, then count diagonally in a loop. This is the traditional way to “ennumerate” the rational numbers.
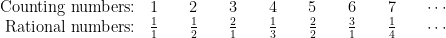
By the way, you can include the negative rationals by doing the same kind of trick that was done to pair up the counting numbers and integers.
Now you can construct a pairing between the rational numbers and the primes:

For those of you considering a career in mathing, be warned. From time to time you may be called upon to say something as bat-shit crazy as “there are exactly as many prime numbers as rational numbers”.
There are infinities objectively bigger than the infinities so far. All of the infinities so far have been “countably infinite”, because they’re the same “size” as the counting numbers. Larger infinities can’t be paired, term by term, with smaller infinities.
Set theorists would call countable infinity “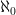 ” (read “aleph null”). Strange as it sounds, it’s the smallest type of infinity.
” (read “aleph null”). Strange as it sounds, it’s the smallest type of infinity.
The size of the set of real numbers is an example of a larger infinity. While rational numbers can be found everywhere on the number line, they leave a lot of gaps. If you went stab-crazy on a piece of paper with an infinitely thin pin, you’d make a lot of holes, but you’d never destroy the paper. Similarly, the rational numbers are pin pricks on the number line. Using a countable infinity you can’t construct any kind of “continuous” set (like the real numbers). You need a bigger infinity.
The number line itself, the real numbers, is a larger kind of infinity. There’s no way to pair the real numbers up with the counting numbers (it’s difficult to show this). The kind of infinity that’s the size of the set of real numbers is called “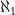 “.
“.
Before you ask: yes, there’s an 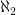 ,
, 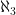 , and so forth, but these are more difficult to picture. To get from one to the next all you have to do is take the “power set” of a set that’s as big as the previous
, and so forth, but these are more difficult to picture. To get from one to the next all you have to do is take the “power set” of a set that’s as big as the previous 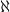 . Isn’t that weird?
. Isn’t that weird?
A commenter kindly pointed out that this “power set thing” is a property of “ numbers” (“beth numbers”). But, if you buy the “generalized continuum hypothesis” you find that
numbers” (“beth numbers”). But, if you buy the “generalized continuum hypothesis” you find that  . This is a bit more technical than this post needs, but it’s worth mentioning.
. This is a bit more technical than this post needs, but it’s worth mentioning.
Quick aside: If A is a set, then the power set of A (written 2A, for silly reasons) is the “set of all subsets of A”. So if A = (1,2,3), then 2A = (Ø, (1), (2), (3), (1,2), (1,3), (2,3), (1,2,3) ). Finite power sets aren’t too interesting, but they make good examples.
Update: The Mathematician was kind enough to explain why the real numbers are the size of the power set of the counting numbers, in the next section.
Strangely enough, there doesn’t seem to be infinities in between these sizes. That is, there doesn’t seem to be an “ ” (e.g., something bigger than
” (e.g., something bigger than 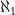 and smaller than
and smaller than 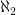 ). This is called the “continuum hypothesis“, and (as of this post) it’s one of the great unsolved mysteries in mathematics. In fact it has been proven that, using the presently accepted axioms of mathematics, the continuum hypothesis can’t be proven and it can’t be dis-proven. This may be one of the “incomplete bits” of logic that Godel showed must exist. Heavy stuff.
). This is called the “continuum hypothesis“, and (as of this post) it’s one of the great unsolved mysteries in mathematics. In fact it has been proven that, using the presently accepted axioms of mathematics, the continuum hypothesis can’t be proven and it can’t be dis-proven. This may be one of the “incomplete bits” of logic that Godel showed must exist. Heavy stuff.
Mathematician: This isn’t rigorous, but gives the intuition perhaps.
Let’s suppose we think of each natural number as representing one binary digit of a number between 0 and 1 (so the nth natural number corresponds to the nth binary digit). Now, the power set is the set of all subsets of the natural numbers, so let’s consider one such subset of the natural numbers. We can think of representing that subset as a binary number, with a 1 for each number in the subset, and a 0 for each number not in the subset. Hence, each element of the power set corresponds to an infinite sequence of binary digits, which can just be thought of as a number between 0 and 1. Then you just need a function from [0,1] to all of the real numbers, like 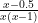 , which leads us to believe that there should be a function mapping each real number into an element of the power set of the natural numbers.
, which leads us to believe that there should be a function mapping each real number into an element of the power set of the natural numbers.
) implies immediately that the ratio is 1-1. I.e., an almighty consciousness capable of everything must necessarily exist. QED