Physicist: It’s a little surprising that this question didn’t come up earlier. Unfortunately, there’s no intuitive way to understand why “the energy of the rest mass of an object is equal to the rest mass times the speed of light squared” (E=MC2). A complete derivation/proof includes a fair chunk of math (in the second half of this post), a decent understanding of relativity, and (most important) experimental verification.
So first, here’s an old physics trick (used by old physicists) to guess answers without doing any thinking or work, and perhaps while drinking. Take everything that could have anything to do with the question (any speeds, densities, sizes, etc.) and put them together so that the units line up correctly. There’s an excellent example in this old post about poo.
Here’s the idea; energy is distance times force (E=DF), and force is mass times acceleration (E=DMA), and acceleration is velocity over time, which is the same as distance over time squared (E = DMD/T2 = MD2/T2).
So energy has units of mass times velocity squared. So, if there were some kind of universal relationship between mass and energy, then it should depend on universal constants. Quick! Name a universal speed! E=MC2
Totally done.
This is a long long way from being a solid argument. You could just as easily have E=5MC2 or E=πMC2 or something like that, and still have the units correct. It may even be possible to mix together a bunch of other universal constants until you get velocity squared, or there may just be a new, previously unknown physical constant involved. This trick is just something used to get a thumbnail sketch of what “looks” like a correct answer, and in this particular case it’s exactly right.
For a more formal derivation, you’d have to stir the answer gravy:
Answer gravy: This derivation is going to seem pretty indirect, and it is. But that’s basically because E = mc2 is an accidental result from a more all-encompassing theory. So bear with me…
The length of regular vectors, (which could be distance, momentum, whatever) remains unchanged by rotations. If you take a stick and just turn it, then of course it stays the same length. The same holds true for speed: 60 mph is 60 mph no matter what direction you’re moving in.
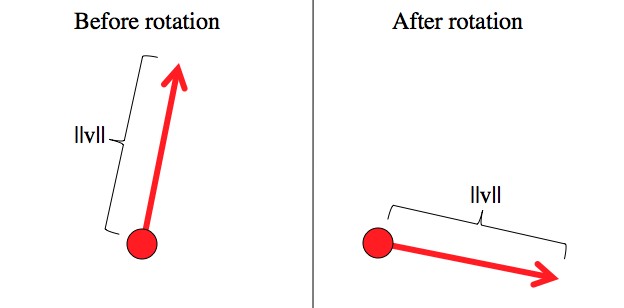
Although the vector, v, changes when you rotate your point of view, its length, ||v||, always stays the same.
If you have a vector (x,y,z), then it’s length is denoted by ““. According to the Pythagorean theorem,
.
When relativity came along, time suddenly became an important fourth component: (x,y,z,t). And the true “conserved distance” was revealed to be: . Notice that when you ignore time (t=0), then this reduces to the usual definition.
This fancy new “spacetime interval” conserves the length of things under ordinary rotations (which just move around the x, y, z part), but also conserves length under “rotations involving time”. In ordinary physics you can rotate how you see things by turning your head. In relativity you rotate how you see things in spacetime, by running past them (changing your speed with respect to what you’re looking at). “Spacetime rotations” (changing your own speed) are often called “Lorentz boosts“, by people who don’t feel like being clearly understood.
You can prove that the spacetime interval is invariant based only on the speed of light being the same to everyone. It’s a bit of a tangent, so I won’t include it here. (Update 8/10/13: but it is included here!)
Some difficulties show up in relativity when you try to talk about velocity. If your position vector is , then your velocity vector is
(velocity is the time derivative of position).
But since relativity messes with distance and time, it’s important to come up with a better definition of time. The answer Einstein came up with was , which is time as measured by clocks on the moving object in question.
is often called “proper time”. So the better definition of velocity is
. This way you can talk about how fast an object is moving through time, as well as how fast it’s moving through space.
By the way, as measured by every one else on the planet, you’re currently moving through their time (t) at almost exactly 1 second per second ().
One of the most important, simple things that you can know about relativity is the gamma function: . You can derive the gamma function by thinking about light clocks, or a couple other things, but I don’t want to side track on that just now.
Among other things, . That is,
is the ratio of how fast “outside time” passes from the point of view of the object’s “on-board time”. So now, using the chain rule from calculus:
.
For succinctness (and tradition) I’ll bundle the first three terms together:
Now check this out! Remember that the spacetime interval for a spacetime vector with spacial component , and temporal component
, is
.
(This used a slight breach of notation: “” is a velocity vector and “
” is the length of the velocity, or “speed”)
The amazing thing about “spacetime speed” is that, no matter what v is, .
(Quick aside; it may concern you that a squared quantity can be negative. Don’t worry about it.)
Now, Einstein (having a passing familiarity with physics) knew that momentum () is conserved, and that the magnitude of momentum is conserved by rotation (in other words, the direction of the momentum is messed up by rotation, but the amount of momentum is conserved (top picture of this post). He also knew that to get from velocity to momentum, just multiply by mass (momentum is
). Easy nuf.
So if ordinary momentum is given by the first term (the “spacial term”): , then what’s that other stuff (
)? Look at the conserved quantity:
What’s interesting here is that m2c2 never changes, and P2 only changes if you start moving. For example, if you were to run as fast as a bullet (in the direction of the bullet), you wouldn’t worry about it hurting you, because from your perspective it has no momentum.
So whatever that last term is () it’s also conserved (as long as you don’t change your own speed). Which is interesting. So the ‘Stein studied its behavior very closely. If you take its Taylor expansion, which turns functions into polynomials, you get this:
The second term there should look kinda familiar (if you’ve taken intro physics); it’s the classical kinetic energy of an object (1/2 mv2) divided by c. Could this whole thing (thought Einstein) be the energy of the object in question, divided by c? Energy is definitely conserved. And, since c is a constant, energy divided by c is also conserved.
So, multiplying by c: .
You can also plug this into and, Alaca-math! You get Einstein’s (sorta) famous energy/momentum relation:
.
Notice that the energy and momentum here are not the classical (Newtonian) energy and momentum: and
. Instead they are the relativistic energy and momentum:
and
. This only has noticeable effects at extremely high speeds, and at lower speeds they look like:
and
, which is what you’d hope for. New theories should always include the old theories as a special case (or disprove them).
Now, holy crap. If you allow the speed of the object to be zero (v=0), you find that everything other than the first term in that long equation for E vanishes, and you’re left with (drumroll): E=mc2! So even objects that aren’t moving are still holding energy. A lot of energy. One kilogram of matter holds the energy equivalent of 21.4 Megatons of TNT, or about 1500 Hiroshima bombs.
The first question that should come to mind when you’ve got a new theory that’s, honestly, pretty insane is “why didn’t anyone notice this before?” Why is it that the only part of the energy that anyone ever noticed was ? Well, the higher terms are a little hard to see. Up until Einstein that fastest things around were bullets moving at about the speed of sound. If you were to use the “
” equation for kinetic energy you would be exactly right up to one part in 20,000,000,000,000,000. All of the higher terms are divided by some power of c (a big number), so until the speed gets ridiculously high they just don’t matter.
But what about the mc2? Well, to be detected energy has to do something. If somebody flings a battery at you, it really doesn’t matter if the battery is charged up or not.
Side note: This derivation isn’t a “proof” per say, just a really solid argument: “there’s this thing that’s conserved according to relativity, and it looks exactly like energy”. However, you can’t, using math alone, prove anything about the outside universe. The “proof” came when E=mc2 was tested experimentally (with particle accelerators ‘n stuff).
But Einstein’s techniques and equations have been verified as many times as they’ve been tested. One of the most profound conclusions is that, literally, “energy is the time component of momentum”. Or “E/c” is at least. So conservation of energy, momentum, and matter are all actually the same conservation law!