My bad: If atoms are mostly made up of empty space, why do things feel solid?

Posted on February 7, 2011 by The Physicist

Physicist: Thanks to a comment in the original post, I did a little research and found that I was wrong, wrong, holy crap wrong.  Here’s some of that comment:

“The source of the ultimate “excluded volume” forces is entirely quantum mechanical: it is the fact that electrons are fermions, hence (this is the Pauli exclusion principle) cannot occupy the same volume without being in different energy states. If you attempt to push the orbital electrons of two atoms into the same volume of space, most of the electrons will need to be promoted to much higher energy states. The requirement of a great deal of energy to move the atoms closer is what we interpret as a force. You might call it an “exclusion” force, because it comes from the exclusion principle —”

One of the nice properties to come out of the depths of quantum physics is the “Pauli Exclusion Principle“.  “Nice”, because it can be understood without a couple years of extra schooling.  Essentially, two “fermions” (which is a classification of particles that includes all ordinary matter: neutrons, protons, and electrons) can’t be in the same state.  That state includes (in the case of electrons in atoms) electron orbitals.

You could argue (successfully) that the Pauli exclusion principle is responsible for all of the complex chemistry of the universe.  If electrons didn’t “stack up” into higher and more complicated shells, then every element would have more or less the same chemical properties as hydrogen and helium.  Instead, as you move along the periodic table, every new electron tries to settle into the lowest possible state, but finds that many of them are occupied.  So, it ends up in a high energy state, because it can’t find any that are lower.

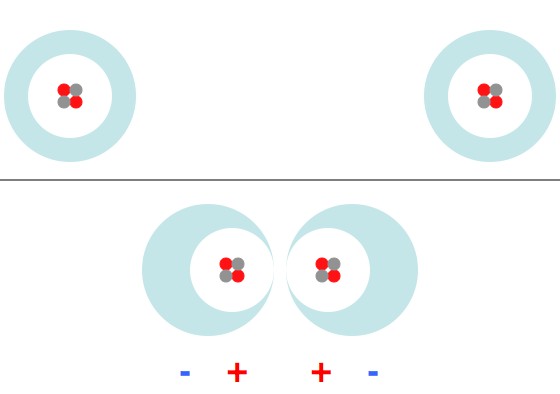
When two atoms are brought very close together their electron orbitals start to overlap and the atoms start to “share” electron orbitals.  In some cases this takes the form of a chemical bond (and the atoms get stuck together).  More often sharing an orbital means that the electrons already present are forced into higher energy orbitals.  By necessity, the effect kicks in when the atoms are close enough that you can’t tell which electron came from which atom (for a few electrons at least).

A good way to define a force is a system’s attempt to get rid of energy (specifically: \vec{F}=-\nabla U, which is just fancy speak for “stuff rolls downhill”).  If the atoms are too close together some electrons find themselves in high-energy states, and if the atoms are a little farther apart those electrons will be in lower energy states.  So, there’s a force that pushes the atoms away from each other, once they get very close together.

So, the repulsion effect isn’t directly caused by electric forces, it’s more of a side effect.  But, if you could somehow “turn up” the strength of the electromagnetic force in our universe, you’d find that the repulsive effect increased in kind, because the amount of energy tied up in the electron’s energy levels is proportional to the strength of the electromagnetic force.

That’s a bit subtle.  It’s a little like saying that when you push a car up a hill (while the car is trying to push you back down the hill), you’re not fighting gravity directly, you’re fighting the effect of gravity on the car.

Posted in -- By the Physicist, Mistake, Quantum Theory | 30 Comments

Q: How many mathematicians/physicists does it take to screw in a light bulb?

Posted on February 5, 2011 by The Physicist

Mathematician:

Theorem (Bulb Screwing)

It only takes one mathematician to screw in a light bulb.

Proof:
Let the “bulb screwing number” N_{p} of a profession p, be the minimum number of people of profession p that must be assembled to screw in a light bulb. For any pair of professions p_{a} and p_{b} with p_{a} \ne p_{b} and N_{p_{b}} finite, there exists a “hiring” operation such that any one person of profession p_{a} can hire a collection of size N_{p_{b}} of appropriate people of profession p_{b} such that the collection of such people can screw in a light bulb. By the transitive property of light bulb screwing with respect to hiring, a single member of profession p_{a} can screw in a light bulb by hiring N_{p_{b}} people of profession p_{b} and therefore, so long as there exists a profession p_{b} \ne p_{a} with finite bulb screwing number, the existence of this hiring operation implies that the bulb screwing number N_{p_{a}} of p_{a} is at most 1. But, since we know there exists at least one light bulb that has been screwed in by at least one person of some non-mathematician profession, and there has only ever been a finite number of people, there must exist some other profession with finite bulb screwing number, so the bulb screwing number for mathematicians is 1. QED

Physicist: The computers capable of accurately doing this simulation haven’t been invented (yet).  So we’ve fallen back on some reasonable approximations, like massless light bulbs and spherical physicists.

So far, it looks like physicists can’t pick up light bulbs, but two physicists can break a bulb between them.

This is probably an NP problem or something, which means that the only remaining option is empirical research.  So, once the NSF frees up the funding for us to hire a team of experimental physicists (to experiment on), build a lab, and buy a light bulb, we’ll have something to publish in a year or two.

Posted in -- By the Mathematician, -- By the Physicist, Brain Teaser, Philosophical | 23 Comments

Q: Why is it that (if you exclude 2 & 3) the difference between the squares of any two prime numbers is divisible by 12?

Posted on January 28, 2011 by The Physicist

Physicist:  That’s a really cool property!

Every prime number (other than 2 and 3) can be written in the form 6j+1 or 6j+5.  For example, 17 = 6(2)+5 and 31 = 6(5)+1.

This is because numbers of the form 6j, 6j+2, 6j+4, are all divisible by 2, and all numbers of the form 6j, 6j+3 are divisible by 3.  So that restricts the options for primes to just the “+1” set and the “+5” set.  Not all of the numbers in these sets are primes, but all the primes are in these two sets.

6j = 6, 12, 18, 24, 30, …  All divisible by 6.

6j+1 = 7, 13, 19, 25, 31, …

6j+2 = 8, 14, 20, 26, 32, …  All divisible by 2.

6j+3 = 9, 15, 21, 27, 33, …  All divisible by 3.

6j+4 = 4, 10, 16, 22, 28, 34, …  All divisible by 2.

6j+5 = 5, 11, 17, 23, 29, 35, …

Call the primes p and q, and notice that p^2-q^2 = (p+q)(p-q).

If p and q are both the same type (+1 or +5), then (p-q) will be a multiple of 6.  For example: (+1 case) 31-7 = 24 and (+5 case) 29-11 = 18.

If p and q are opposite types, then (p+q) will be divisible by 6.  For example: 23+13 = 36.

In both cases, the other bubble, (p+q) or (p-q), will always be divisible by 2, since the sum and difference of any two odd numbers is always even. So, one bubble is always a multiple of 6 and the other is always a multiple of 2, and together the whole thing is always a multiple of 12.

For example: p=11, q=7.  11^2 - 7^2 = (11+7)(11-7) = (18)(4)  18 is divisible by 6, and 4 is divisible by 2, so 18×4 is divisible by 12!

This is another example of modular arithmetic.  It almost should have been included in the “tricks with 9’s post“.

Also: This trick doesn’t really have much to do with “primes”, so much as it has to do with “numbers that don’t have 2 or 3 as a factor”.  That isn’t obvious at first.  The first composite (not prime and not 1) number with no 2’s or 3’s is 25.

Posted in -- By the Physicist, Brain Teaser, Math, Number Theory | 8 Comments

Q: Why does relativistic length contraction (Lorentz contraction) happen?

Posted on January 27, 2011 by The Physicist

Physicist: This probably should have come before the last post.

Length contraction is a symptom of “tilted now planes”.  For someone moving past you events physically in front of them happen earlier than they should (according to you), and events physically behind them happen later (according to you).

Here’s the idea in a nutshell: you’re in the middle of a train when the front and back are hit by lightning.  People on the train will see the lightning at the front of the train a little earlier than someone on the tracks because they’re moving toward it, and will see the lightning at the back of the train a little later because they’re moving away from it.  At least, that’s the way someone on the tracks would explain it.

However, the laws of physics are blind to “uniform movement”.  That is, all physical laws are exactly the same whether you’re moving (at a constant speed) or not.  And that’s relativity.  So both points of view are equally correct.  That summary was a little fast because it’s covered in a lot more detail here: Q: According to relativity, two moving observers always see the other moving through time slower. Isn’t that a contradiction? Doesn’t one have to be faster?

Someone of the tracks (blue) sees lightning hit the front and back of a train, simultaneously, as it passes by. Someone on the train (red) sees the lightning at the front first. Both are right. So, in general (not just with lightning), when someone passes by events happening physically in front of them happen a little sooner than they should (according to you).

The traditional example is the barn-running pole-vaulter thought experiment.

A pole vaulter runs through a barn very, very fast with a pole that (when it’s standing still) is about as long as the barn.  From her point of view the barn, which is rushing past her, is contracted so that her pole (briefly) is sticking out of both ends of the barn.  The farmer, who leaves the doors to his barn open, because this happens all the time, sees the vaulter and her pole contracted so that (briefly) the entire pole is inside the barn.

They’re both right, and here’s why!  Consider the two events (A) the back of the pole entering the barn and (B) the front of the pole exiting the barn.

For the farmer event A happens first, then event B happens second.

For the farmer the back of the pole enters the barn before the front of the pole exits the barn. Obviously, the pole shrank.

The pole vaulter sees the same process, but sees the events in front of her happening sooner, and the events behind her happening later.  So, in this case, she sees event B first and event A second.

For the pole vaulter the front of the pole exits the barn first, and then the back of the pole enters the barn. Obviously, the barn shrank.

So, time dilation, length contraction, and the rearrangement of events are just three sides of the same weirdly shaped coin.

I should point out, that there’s a weakness in the language that makes it sound like relativistic effects aren’t real events; “from one point of view…”, “when one person looks at the other they see…”, etc.  Length contraction is a completely real effect.  At very high speeds objects really do contract in the direction of motion.  However, you have to be really trucking along before it becomes an issue.  What follows is answer gravy.

Answer gravy: The best way to describe how strong relativistic effects are is to use “\gamma” (“gamma”), and \gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} where “c” is the speed of light and “v” is the relative speed of the object in question.  The amount that the mass is multiplied, the amount that time slows, and the amount that length contracts, are all \gamma.  Gamma is such a useful measure, that you’ll often hear physicists refer to things “moving with a gamma of ___”, instead of stating the actual speed.

That whole opening it to explain why relativistic effects are so unnoticable.  Below is a graph of speed on the x-axis (from 0 to c) and gamma on the y-axis.  Just to put things in perspective I’ve included some sample speeds, that people have experienced.

No one has ever experienced a relativistic effect that they could feel. We can measure the effects, but the effects are extremely small on the everyday scale. The horizontal line is "gamma = 1".

The Apollo 10 service and crew modules (the fastest manned vehicle ever) managed to get all the way up to 0.0037% of light speed, which is just unimaginably fast.  Commander Stafford, et al., experienced a \gamma of approximately \gamma = 1.00000000068.  So from the perspective of everyone on the ground, the 11.03m long module shrank by approximately 7.5 nanometers.

More gravy!: Mathematically, the way a physicist might describe length contraction (more exactly) would be to use the “spacetime interval“.  If you have two events happening at the points (x_1, y_1, z_1) and (x_2, y_2, z_2), at the times t_1 and t_2.  The spacetime interval, S, is defined as:

S^2= c^2(t_2-t_1)^2-(x_1-x_2)^2 -(y_1-y_2)^2 -(z_1-z_2)^2 = c^2(\Delta t)^2-(\Delta x)^2-(\Delta y)^2-(\Delta z)^2

S is useful because, although relativistic effects change the x’s and t’s and whatnot, S remains constant for everybody.  Here goes!

When something is sitting still the way you measure it is to get out a ruler.  When something is moving past you the way to measure it’s length is to time how long it takes to get past a point.  If it’s moving at 10 kph and it takes 2 hours to pass, then it must be 20 km long.  So, we have two events.  When the front of the object passes the measuring point, and when the back of the object passes the measuring point.

The length of an object in the frame where something is sitting still, we’ll call “L”.  When something is moving it’s length is LM.

An object moving past an arbitrary point used for measurement. In the objects stationary frame the arrow is doing the moving, and in the arrows frame the object is doing the moving.

In the stationary frame:

S^2 = c^2(\Delta t)^2 - (\Delta x)^2 = c^2 \left( \frac{L}{v} \right)^2 - L^2 = L^2 \left( \frac{c^2}{v^2}-1\right).  That is, the distance between is just the length, and the time between is how long it takes for the measuring point to traverse that distance.

Similarly, in the moving frame:

S^2 = c^2(\Delta t^\prime)^2 - (\Delta x^\prime)^2 = c^2 \left( \frac{L_M}{v} \right)^2 - 0^2 = \frac{c^2}{v^2} L_M^2.  That is, the events happen in the same place, but at different times given by how long it takes the object (now LM long) to pass.  The primes (the ” ‘ “) are to indicate that the position and time are different in the new frame.

But, the spacetime interval is always the same, even if everything else is different.  So:

\begin{array}{ll}\frac{c^2}{v^2} L_M^2 = S^2 = L^2 \left( \frac{c^2}{v^2}-1\right)\\\Rightarrow L_M^2 = L^2 \left(1- \frac{v^2}{c^2}\right)\\\Rightarrow L_M = L \sqrt{1- \frac{v^2}{c^2}}\\\Rightarrow L_M = L\frac{1}{\gamma}\end{array}

Gamma again!  Good times!

Posted in -- By the Physicist, Physics, Relativity | 24 Comments

Q: Why does Lorentz contraction only act in the direction of motion?

Posted on January 23, 2011 by The Physicist

Physicist: A lot of things get messed up by relativity, like when and where stuff happens, how massive things are, or how time passes.  Length contraction is an effect that literally makes things shorter in the direction of motion.  So if something whipped by you from left to right it would be thinner, but just as tall.

"Lorentz contraction" or "length contraction": Moving objects are shorter in the direction of motion. As with all relativistic effects, this mostly shows up close to the speed of light, C. It is physically real, and not an illusion or trick-of-the-light.

Which begs the question, why is it just as tall?  Why doesn’t it just shrink all over, or something?

Well, one of the things that relativity doesn’t change is whether or not an “event” actually happens.  So imagine this: you’ve got two hoops spanned by paper, and they’re flying at each other face-on.  If the paper in a hoop is torn out, then you’ve got an event that everyone will agree on.  No matter where you are or how fast you’re moving, you’ll see that the paper was torn.  The only thing relativity affects is when and where that event takes place.

So, pretend that length contraction now shrinks things in every direction.

If you assume that length contraction acts perpendicular to the direction of motion you end up with people explicitly disagreeing over events, in a paradoxical kind of way.

If you’re in the reference frame of the green hoop (from your point of view the green hoop is sitting still), then the purple hoop will be smaller and will pass through.  The green hoop’s paper will burst, and the purple’s will stay intact.  If you’re in the purple hoop’s frame, exactly the opposite happens.  And finally, if you’re exactly in between the two frames (you see each hoop approaching at the same speed), both hoops shrink by the same amount and run into each other.

What should be a single event, viewed from different perspectives, is now three different and contradictory events.  You can make the effectively identical arguments for enlarging in the perpendicular direction, and even rotation.

Perpendicular special relativistic effects lead to basic contradictions and paradoxes.

Posted in -- By the Physicist, Physics, Relativity | 22 Comments

Q: If atoms are mostly made up of empty space, why do things feel solid?

Posted on January 19, 2011 by The Physicist

Physicist:

(The following paragraph is wrong.  Like, really wrong.  There’s a redaction here: My bad: If atoms are mostly made up of empty space, why do things feel solid?)

As atoms get too close to one another their charges begin to repel each other.  Once they’re close enough that they can “see” the other atom, the electrons on the near side of both atoms begin to repel each other and move more to the far side of both atoms.  This leaves the positively charged nuclei facing each other.

Electrons swarm around the nuclei of their atoms (in this case Helium 4). When they're brought very close together the electron clouds shift and the atoms briefly polarize in such a way that they repel.

Basically, when two atoms come too close they behave exactly like magnets brought together with the “north” ends pointing together.

(Everything up to here has been wrong.)

This certainly isn’t the whole story.  Quantum chemistry isn’t rocket science, but it’s still pretty complicated.  Atoms can share electrons, or their electrons can move so that they behave like attracting magnets, and a whole mess of other things.  For example, attractive van der Waal forces can show up when atoms are close, but not too close.  Slight fluctuations in the arrangement of electrons in one atom induces a sympathetic arrangement in nearby atoms (this is more specifically a “London dispersion force“).  As a result, the atoms end up with dipoles lined up in a “+-  +-” way, instead of a “-+  +-” way, like in the picture above.

In general, the force is extremely small.  But it is just strong enough to hold liquid helium to itself (otherwise it would be a gas), and hold geckos to walls.

Geckos have weird feet because they have evolved to optimize the chance of random dipole interactions between the atoms in their feet and the atoms of whatever they're climbing. As a result, they can climb vetically on materials as smooth as glass. Pictured here is a gecko excited to learn that someone remembered his birthday.

Addressing the fact that matter is mostly empty space, if you really squeeze matter you’ll find that the electrical forces can no longer hold atoms apart.  Basically, they find that it’s easier for the electrons and protons to fuse together and form neutrons.  Once all the charges are out of the way the atoms (now balls of neutrons) are free to collapse together.  At that point the only thing holding them apart is “Pauli pressure”, which is fancy quantum physics speak for “they can’t be in the same place”.

The only time this happens in nature is in neutron stars.  To get an idea for what happens when you “deflate” matter: If you were to crush a 50m Olympic size swimming pool into neutron star material, it would be about 0.05mm long, which is about the width of a single hair.

Posted in -- By the Physicist, Particle Physics, Physics | 72 Comments